相信提到斐波那契数列,大家都不陌生,这个是在我们学习 C/C++ 的过程中必然会接触到的一个问题,而作为一个经典的求解模型,我们怎么能少的了去研究这个模型呢?笔者在不断地学习和思考过程中,发现了这类经典模型竟然有如此多的有意思的求解算法,能让这个经典问题的时间复杂度降低到 (O(1)) ,下面我想对这个经典问题的求解做一个较为深入的剖析,请听我娓娓道来。
我们可以用如下递推公式来表示斐波那契数列 (F) 的第 (n) 项:
回顾一下我们刚开始学 (C) 语言的时候,讲到函数递归那节,老师总是喜欢那这个例子来说。
斐波那契数列就是像蜗牛的壳一样,越深入其中,越能发觉其中的奥秘,形成一条条优美的数学曲线,就像这样:

递归在数学与计算机科学中,是指在函数的定义中使用函数自身的方法,可能有些人会把递归和循环弄混淆,我觉得务必要把这一点区分清楚才行。
递归查找
举个例子,给你一把钥匙,你站在门前面,问你用这把钥匙能打开几扇门。
递归:你打开面前这扇门,看到屋里面还有一扇门(这门可能跟前面打开的门一样大小,也可能门小了些),你走过去,发现手中的钥匙还可以打开它,你推开门,发现里面还有一扇门,你继续打开。若干次之后,你打开面前一扇门,发现只有一间屋子,没有门了。 你开始原路返回,每走回一间屋子,你数一次,走到入口的时候,你可以回答出你到底用这钥匙开了几扇门。
循环:你打开面前这扇门,看到屋里面还有一扇门,(这门可能跟前面打开的门一样大小,也可能门小了些),你走过去,发现手中的钥匙还可以打开它,你推开门,发现里面还有一扇门,(前面门如果一样,这门也是一样,第二扇门如果相比第一扇门变小了,这扇门也比第二扇门变小了),你继续打开这扇门,一直这样走下去。 入口处的人始终等不到你回去告诉他答案。
简单来说,递归就是有去有回,循环就是有去无回。
我们可以用如下图来表示程序中循环调用的过程:
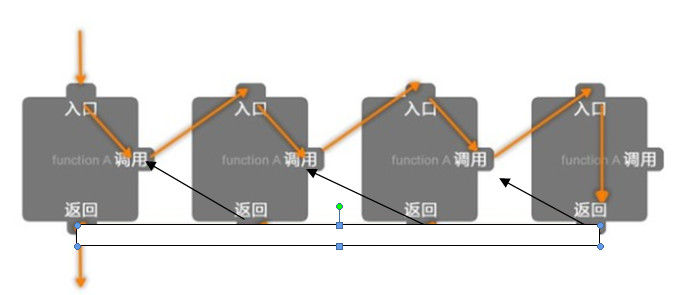
于是我们可以用递归查找的方式去实现上述这一过程。
时间复杂度:(O(2^n))
空间复杂度:(O(1))
/**
递归实现
*/
int Fibonacci_Re(int num){
if(num == 0){
return 0;
}
else if(num == 1){
return 1;
}
else{
return Fibonacci_Re(num - 1) + Fibonacci_Re(num - 2);
}
}
线性递归查找
It's amazing!!!如此高的时间复杂度,我们定然是不会满意的,该算法有巨大的改进空间。我们是否可以在某种意义下对这个递归过程进行改进,来优化这个时间复杂度。还是从上面这个开门的例子来讲,我们经历了顺路打开门和原路返回数门这两个过程,我们是不是可以考虑在边开门的过程中边数我们一路开门的数量呢?这对时间代价上会带来极大的改进,那我们想想看该怎么办呢?
为消除递归算法中重复的递归实例,在各子问题求解之后,及时记录下其对应的解答。比如可以从原问题出发自顶向下,每当遇到一个子问题,都首先查验它是否已经计算过,以此通过直接调阅纪录获得解答,从而避免重新计算。也可以从递归基出发,自底而上递推的得出各子问题的解,直至最终原问题的解。前者即为所谓的制表或记忆策略,后者即为所谓的动态规划策略。
为应用上述的制表策略,我们可以从改造 (Fibonacci) 数的递归定义入手。我们考虑转换成如下的递归函数,即可计算一对相邻的Fibonacci数:
((Fibonacci \_ Re(k-1),Fibonacci \_ Re(k-1))),得到如下更高效率的线性递归算法。
时间复杂度:$ O(n) $
空间复杂度:$ O(n) $
/**
线性递归实现
*/
int Fibonacci_Re(int num, int& prev){
if(num == 0){
prev = 1;
return 0;
}
else{
int prevPrev;
prev = Fibonacci_Re(num - 1, prevPrev);
return prevPrev + prev;
}
}
该算法呈线性递归模式,递归的深度线性正比于输入 (num) ,前后共计仅出现 (O(n)) 个实例,累计耗时不超过 (O(n))。遗憾的是,该算法共需要使用 (O(n)) 规模的附加空间。如何进一步改进呢?
减而治之
若将以上逐层返回的过程,等效地视作从递归基出发,按规模自小而大求解各子问题的过程,即可采用动态规划的过程。我们完全可以考虑通过增加变量的方式代替递归操作,牺牲少量的空间代价换取时间效率的大幅度提升,于是我们就有了如下的改进方式,通过中间变量保存 (F(n-1)) 和 (F(n-2)),利用元素的交换我们可以实现上述等价的一个过程。此时在空间上,我们由 (O(1)) 变成了 (O(4)),由于申请的空间数量仍为常数个,我们可以近似的认为空间效率仍为 (O(1))。
时间复杂度:(O(n))
空间复杂度:(O(1))
/**
非递归实现(减而治之1)
*/
int Fibonacci_No_Re(int num){
if(num == 0){
return 0;
}
else if(num == 1){
return 1;
}
else{
int a = 0;
int b = 1;
int c = 1;
while(num > 2){
a = b;
b = c;
c = a + b;
num--;
}
return c;
}
}
我们甚至还可以对变量的数量进行优化,将 (O(4)) 变成了 (O(3)),减少一个单位空间的浪费,我们可以实现如下这一过程:
/**
非递归实现(减而治之2)
*/
int Fibonacci_No_Re(int num){
int a = 1;
int b = 0;
while(0 < num--){
b += a;
a = b - a;
}
return b;
}
分而治之(二分查找)
而当我们面对输入相对较为庞大的数据时,每每感慨于头绪纷杂而无从下手的你,不妨先从孙子的名言中获取灵感——“凡治众如治寡,分数是也”。是的,解决此类问题的最有效方法之一,就是将其分解为若干规模更小的子问题,再通过递归机制分别求解。这种分解持续进行,直到子问题规模缩减至平凡情况,这也就是所谓的分而治之策略。
与减而治之策略一样,这里也要求对原问题重新表述,以保证子问题与原问题在接口形式上的一致。既然每一递归实例都可能做多次递归,故称作为多路递归。我们通常都是将原问题一分为二,故称作为二分递归。
按照二分递归的模式,我们可以再次求和斐波那契求和问题。
时间复杂度:$O(log(n)) $
空间复杂度:$ O(1) $
/**
二分查找(递归实现)
*/
int binary_find(int arr[], int num, int arr_size, int left, int right){
assert(arr);
int mid = (left + right) / 2;
if(left <= right){
if(num < arr[mid]){
binary_find(arr, num, arr_size, left, mid - 1);
}
else if(num > arr[mid]){
binary_find(arr, num, arr_size, mid + 1, right);
}
else{
return mid;
}
}
}
当然我们也可以不采用递归模式,按照上面的思路,仍采用分而治之的模式进行求解。
时间复杂度:$ O(log(n)) $
空间复杂度:$ O(1) $
/**
二分查找(非递归实现)
*/
int binary_find(int arr[], int num, int arr_size){
if(num == 0){
return 0;
}
else if(num == 1){
return 1;
}
int left = 0;
int right = arr_size - 1;
while(left <= right){
int mid = (left + right) >> 1;
if(num > arr[mid]){
left = mid + 1;
}
else if(num < arr[mid]){
right = mid - 1;
}
else{
return mid;
}
}
return -1;
}
矩阵快速幂
为了正确高效的计算斐波那契数列,我们首先需要了解以下这个矩阵等式:
为了推导出这个等式,我们首先有:
随即得到:
同理可得:
所以:
又由于(F(1) = 1),(F(0) = 0),(F(-1) = 1),则我们得到了开始给出的矩阵等式。当然,我们也可以通过数学归纳法来证明这个矩阵等式。等式中的矩阵
被称为斐波那契数列的 (Q)- 矩阵。
通过 (Q)- 矩阵,我们可以利用如下公式进行计算 (F_n):
如此一来,计算斐波那契数列的问题就转化为了求 (Q) 的 (n-1) 次幂的问题。我们使用矩阵快速幂的方法来达到 (O(log(n))) 的复杂度。借助分治的思想,快速幂采用以下公式进行计算:
实现过程如下:
时间复杂度:(O(log(n)))
空间复杂度:(O(1))
//矩阵数据结构定义
#define MOD 100000
struct matrix{
int a[2][2];
}
//矩阵相乘函数的实现
matrix mul_matrix{
matrix res;
memset(res.a, 0, sizeof(res.a));
for(int i = 0; i < 2; i++){
for(int j = 0; i < 2; j++){
for(int k = 0; k < 2; k++){
res.a[i][j] += x.a[i][k] * y.a[k][j];
res.a[i][j] %= MOD;
}
}
}
return res;
}
int pow(int n)
{
matrix base, res;
//将res初始化为单位矩阵
for(int i = 0; i < 2; i++){
res.a[i][i] = 1;
}
//给base矩阵赋予初值
base.a[0][0] = 1;
base.a[0][1] = 1;
base.a[1][0] = 1;
base.a[1][1] = 0;
while(n > 0)
{
if(n % 2 == 1){
res *= base;
}
base *= base;
n >>= 1;//n = n / 2;
}
return res.a[0][1];//或者a[1][0]
}
对于斐波那契数列,我们还有以下这样的递推公式:
为了得到以上递归式,我们依然需要利用 (Q)- 矩阵。由于 $ Q^m Q^n = Q^{m+n} $,展开得到:
将该式中 (n) 替换为 (n+1) 可得:
在如上两个等式中令 (m=n),则可得到开头所述递推公式。利用这个新的递归公式,我们计算斐波那契数列的复杂度也为 (O(log(n))),并且实现起来比矩阵的方法简单一些:
时间复杂度:(O(log(n)))
空间复杂度:(O(1))
int Fibonacci_recursion_fast(int num){
if(num == 0){
return 0;
}
else if(num == 1){
return 1;
}
else{
int k = num % 2 ? (num + 1) / 2 : num / 2;
int fib_k = Fibonacci_recursion_fast(k);
int fib_k_1 = Fibonacci_recursion_fast(k - 1);
return num % 2 ? power(fib_k, 2) + power(fib_k_1, 2) : (2 * fib_k_1 + fib_k) * fib_k;
}
}
公式法
我们还有没有更快的方法呢?对于斐波那契数列这个常见的递推数列,其第 (n) 项的值的通项公式如下:
既然作为工科生,那肯定要用一些工科生的做法来证明这个公式呀,嘿嘿,下面开始我的表演~
我们回想一下,斐波那契数列的所有的值可以看成在数轴上的一个个离散分布的点的集合,学过数字信号处理或者自动控制原理的同学,这个时候,我们很容易想到用Z变换来求解该类问题。
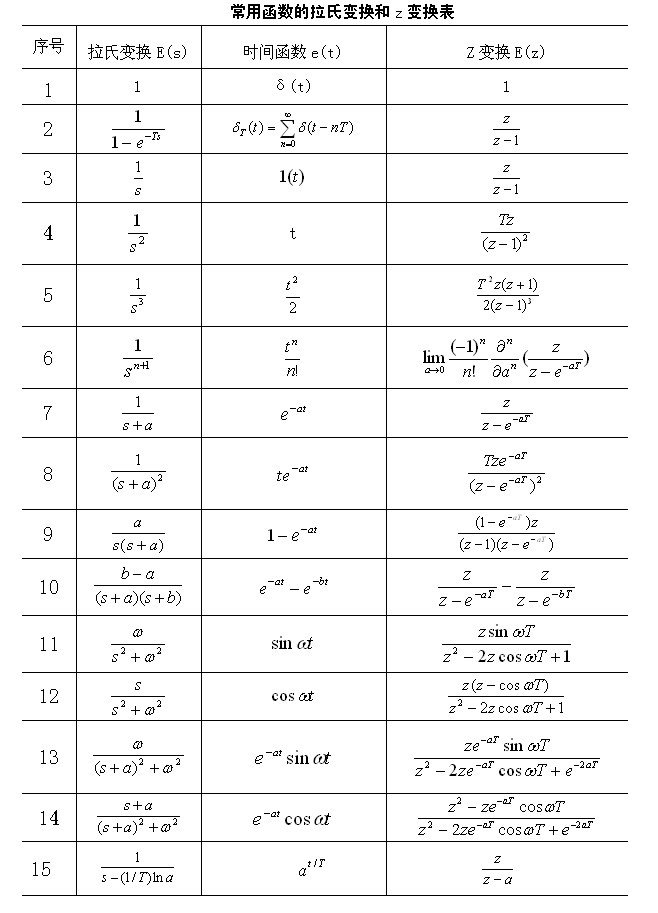
(Z) 变换常用的规则表如下:
当 (n>1) 时,由 (f(n) = f(n-1) + f(n-2)) (这里我们用小写的 (f) 来区分):
由于 (n >= 0),所以我们可以把其表示为(f(n+2) = f(n+1) + f(n)),其中 (n >= 0)。
所以我们利用上式前向差分方程,两边取 (Z) 变换可得:
所以有:
又 (f(0) = 0,f(1) = 1),整理可得:
我们取 (Z) 的逆变换可得:
我们最终可以得到如下通项公式:
更多的证明方法可以参考知乎上的一些数学大佬:https://www.zhihu.com/question/25217301
实现过程如下:
时间复杂度:(O(1))
空间复杂度:(O(1))
/**
纯公式求解
*/
int Fibonacci_formula(int num){
double root_five = sqrt(5 * 1.0);
int result = ((((1 + root_five) / 2, num)) - (((1 - root_five) / 2, num))) / root_five
return result;
}
该方法虽然看起来高效,但是由于涉及大量浮点运算,在 (n) 增大时浮点误差不断增大会导致返回结果不正确甚至数据溢出。