浅谈错排公式的推导及应用

近期学弟在HDU刷题时遇到了关于错排公式的一些问题，我作为过来人就写这篇博客来指导他们~~~

错排的定义：一段序列中一共有n个元素，那么可知这些元素一共有n!种排列方法。假如在进行排列时，原来所有的元素都不在原来的位置，那么称这个排列为错排。而错排数所指的就是在一段有n个元素的序列中，有多少种排列方式是错排。

递归关系：D(n)=(n-1)(D(n-1)+D(n-2))  特别地有D(1)=0,D(2)=1；

错排公式：D(n)=(n!)[(-1)^0/0!+(-1)^1/(1!)+(-1)^2/(2!)+(-1)^3/(3!)+......+(-1)^n/(n!)]；   其中n!=n*(n-1)*(n-2)*......3*2*1      特别地有0!=1  1!=1

首先来对递归公式进行解释：

n个不同的元素的一个错排公式可以分作两步完成：

第一步：假设我们错排第一个元素，那么它可以从2~n的位置任意选择其中的一个，一共是有n-1种选择。

第二步：错排其余n-1个元素，也是需要分情况和种类的。因为这需要看第一步的结果，如果第一个元素落在第k个位置上，第二步就需要把k号元素进行错排，k号元素错排位置的不同将导致不同的情况会发生：

1.假设k号元素正好落在了第一个元素的位置，那么就可以将第一个元素和第k个元素完全剔除出去，因为相当于只是他们两者互换了位置，其他元素暂时还没有发生变动。留下来的n-2元素进行错排的话，那么我们就可以得到了D(n-2)种 的错排方式。

2.若k号元素不排到第一个元素的位置，我们可以暂时将现在排在k号位置的第一个元素剔除出去，生下来的就只包含k号元素和原来n-2个的元素了。这时，我们可以将原来的第一个元素的位置看做是现在k号元素的原本位置，因为k号元素不能够放在原来的位置上，所以就相当于是原来的n-2个元素和k共计n-1个元素进行完全的错排。那么一共就有D(n-1)种方法。 第二种情况希望大家仔细理解！配一张图便于理解

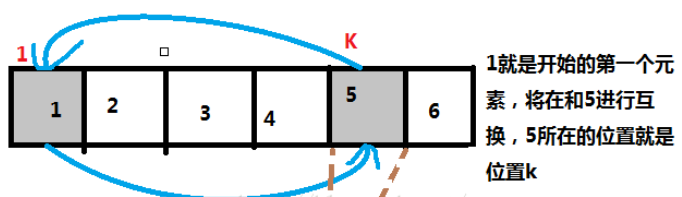
那么，我们有根据加法原理，完成第二步有D(n-2)+D(n-1)种方法。

根据乘法原理得到D(n)=(n-1)(D(n-1)+D(n-2)) 。递推关系解释完毕。

下面我们来推一下错排公式

前提假设D(n)=n!N(n) 那么我们根据上面的递推公式可以得到n!N(n)=(n-1)[(n-2)!N(n-2)+(n-1)!N(n-1)]，等式右边合并一下，我们可以得到

n!N(n)=(n-1)!N(n-2)+(n-1)!N(n-1)同时消去(n-1)!可以得到nN(n)=N(n-2)+N(n-1)

 所以就有两边同时减去nN(n-1)得到：nN(n)-nN(n-1)=(n-1)N(n-1)+N(n-2)-nN(n-1)  即有：n(N(n)-N(n-1))=-N(n-1)+N(n-2)

即为(N(n)-N(n-1))/(N(n-1)-N(n-2))=(-1)/n;

同理有(N(n-1)-N(n-2))/(N(n-2)-N(n-3))=(-1)/(n-1);

            (N(n-2)-N(n-3))/(N(n-3)-N(n-4))=(-1)/(n-2);

            ......

            (N(3)-N(2))/(N(2)-N(1))=(-1)/3;

一共我们得到了n-2个等式，我们可以让左边的等式相乘，右边的等式相乘，因为相消，那么我们可以得到的等式是

(N(n)-N(n-1))/(N(2)-N(1))=(-1)^(n-2)/[n*(n-1)*(n-2)*(n-3)*......4*3]    等式1

又因为(-1)^(n-2)=(-1)^(n) 等式2并且N(2)=D(2)/2!=1/2   N(1)=D(1)/1!=0  所以有N(2)-N(1)=1/2 等式3 将这两个等式2和3带入到上面等式1中我们可以得到：

N(n)-N(n-1)=(-1)^n/[n*(n-1)*(n-2)*(n-3)*......*4*3*2]    即为：N(n)-N(n-1)=(-1)^n/n!

所以有N(n)=(-1)^2/2!+...(-1)^(n-1)/(n-1)!+(-1)^n/n!      又因为存在关系D(n)=n!N(n) 

得到D(n)=n![(-1)^2/2!+...(-1)^(n-1)/(n-1)!+(-1)^n/n! ]    得证

错排公式的应用：

n封信放入n个信封，要求全部放错，共有多少种放法，记n个元素的错排总数为f(n)

方法一：

某人写了n封信和n个信封，如果所有的信都装错了信封。求所有的信都装错信封,共有多少种不同情况。 

当N=1和2时，易得解～，假设F(N-1)和F(N-2)已经得到，重点分析下面的情况：

1.当有N封信的时候，前面N-1封信可以有N-1或者 N-2封错装。

2.前者，对于每一种错装，可以从N-1封信中任意取一封和第 N封错装，故=F(N-1) * (N-1)。

3.后者简单，只能是没装错的那封信和第N封信交换信封，没装错的那封信可以是前面N-1封信中的任意一个，故= F(N-2) * (N-1)。

基本形式：d[1]=0;   d[2]=1 递归式：d[n]= (n-1)*( d[n-1] + d[n-2])

方法二：

假设有n封信，第一封信可放在(2-n)的任一个信封里，共n-1种放法，设第一封信放在了第k个信封里，若此时第k封信放在了第1个信封里，则只要将剩下的n-2错排，即f(n-2)，若第k封信没有放在了第1个信封里，可将第1封信的位置看成是“第k个位置”，即将n-1封信错排，即为f(n-1)

由递推可得,f(n)=(n-1)*(f(n-1)+f(n-2))

以下是程序实现：

#include<stdio.h>
int fun(int);
int main()
{
    int n,res;
    printf("input a number:");
    scanf("%d",&n);
    res=fun(n);
    printf("There are %d cases.
",res);
    return 0;
}
int fun(int n)
{
    if(n==1)
        return 0;
    if(n==2)
        return 1;
    return (n-1)*(fun(n-1)+fun(n-2));
}