D15-图[Java数据结构和算法]

1.图的基本介绍

　　1.1 图是一种数据结构，其中节点可以具有0个或多个相邻元素，两个节点之间的连接称为边，节点也可称为顶点；

　　1.2 图的表示方式：二维数组表示（邻接矩阵），链表表示（邻接表）

　　（1）邻接矩阵：邻接矩阵表示图形中顶点之间相邻关系的矩阵，对于n个顶点的图而言，矩阵是row和col表示的1...n个点；

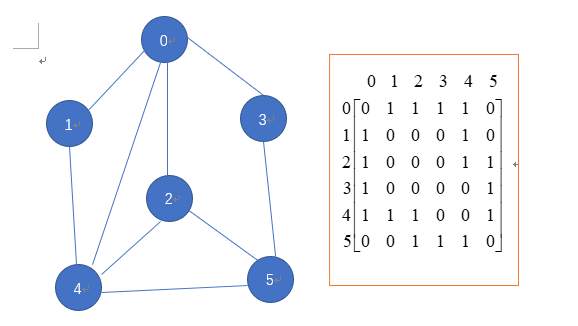
　　　　邻接矩阵需要为每个顶点都分配n个边的空间，其实很多边是不存在的，因此会造成空间的一定损失；

　　（2）邻接表：邻接表的实现只关心存在的边，不关心不存在的边，邻接表由数组+链表组成；

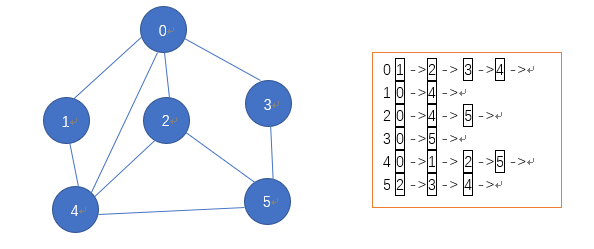
　　　　说明：标记为0的节点相关联的节点为1 2 3 4；

2.图的快速入门

　　2.1 代码实现下图结构

　　2.2 思路分析

　　（1）存储顶点String 使用ArrayList，保存矩阵int[][] edges

 

3. 图遍历：对图的节点进行遍历，有两种访问方式：深度优先遍历和广度优先遍历

　　3.1 深度优先（Depth First Search）基本思想

　　（1）从初始访问节点出发，初始访问节点可能有多个邻接几点，深度优先遍历的策略是首席按访问第一个邻接节点，然后再以这个被访问的邻接节点作为初始节点，访问它的第一个邻接节点，可以理解为每次都在访问完当前节点后首先访问当前节点的第一个邻接节点；

　　（2）纵向挖掘深入；

　　（3）是一个递归的过程；

　　3.2 深度优先遍历算法步骤

　　（1）访问初始节点V，并标记节点V已经被访问；

　　（2）查找节点V的第一个邻接节点W；

　　（3）如果W不存在，返回到节点V，回到步骤1，从初始节点V的下一个节点继续；

　　（4）如果W没有被访问，将W当作V，继续进行步骤１，２，３；

　　（５）如果W已经被访问，查找节点W的邻接节点，转到步骤３；

　　3.2 广度优先（Broad FirstSearch）基本思想

　　类似于一个分层搜索的过程，广度优先遍历需要使用一个队列以保持访问过的节点的顺序，以便按照这个顺序来访问这些节点的邻接节点；

　　3.3 广度优先遍历算法步骤

　　（1）访问初始节点V，并标记节点V已经被访问；

　　（2）节点V入队列；

　　（3）当队列不为空时，继续执行，否则算法结束；

　　（4）出队列，得到队头节点U；

　　（5）查找节点U的第一个邻接节点；

　　（6）若节点U的邻接节点W不存在，则转到步骤3；否则继续执行

　　　　（6.1）若节点W未被访问，则标记其被访问；

　　　　（6.2）节点W入队列；

　　　　（6.3）W若被访问过，查找节点U的继W邻接节点后的下一个邻接节点W，转到步骤6；     

 　　3.4 源代码

package cn.atguigu.graph;

import java.util.ArrayList;
import java.util.Arrays;
import java.util.LinkedList;
import java.util.Queue;

public class Graph {
    //存储顶点的集合
    private ArrayList<String> vertexList;
    //存储图对应的邻接矩阵
    private int[][] edges;
    //表示边的数目
    private int numOfEdges;
    //定义数组boolean[] 记录某个节点是否被访问
    private boolean[] isVisited;
    
    public static void main(String[] args) {
        // 测试图是否创建正确
        int n=5;
        String VertexValue[]= {"A","B","C","D","E"};
        Graph graph=new Graph(n);
        //循环添加顶点
        for (int i = 0; i < VertexValue.length; i++) {
            graph.insertVertex(VertexValue[i]);
        }
        //添加边
        graph.insertEdge(0, 1, 1);
        graph.insertEdge(0, 2, 1);
        graph.insertEdge(1, 2, 1);
        graph.insertEdge(1, 3, 1);
        graph.insertEdge(1, 4, 1);
        
        //graph.showGraph();
        System.out.println("广度遍历");
        graph.bfs();
    }
    
    //构造器
    public Graph(int n) {
        //初始化矩阵和vertexList
        edges=new int[n][n];
        vertexList=new ArrayList<String>();
        numOfEdges=0;
        isVisited=new boolean[n];
    }
    //得到第一个邻接节点的下标
    /**
     * 
     * @param index
     * @return 如果存在就返回对应的下标，否则返回-1
     */
    public int getFirstNeighbor(int index) {
        for (int i = 0; i < vertexList.size(); i++) {
            if(edges[index][i]>0) {
                return i;
            }
        }
        return -1;
    }
    
    //根据前一个邻接节点的下标，获取下一个邻接节点
    public int getNextNeighbor(int v1,int v2) {
        for (int i = v2+1; i < vertexList.size(); i++) {
            if(edges[v1][i]>0) {
                return i;
            }
        }
        return -1;
    }
    //重写广度优先遍历
    public void bfs() {
        for (int i = 0; i < getNumOfVertex(); i++) {
            if(!isVisited[i]) {
                bfs(isVisited, i);
            }
        }
    }
    
    //广度优先遍历算法
    private void bfs(boolean[] isVisited,int i) {
        int u;//表示队列的头节点对应的下标
        int w;//表示邻接节点W
        //队列，记录节点访问顺序
         LinkedList queue=new LinkedList();
        //访问该节点，直接输出
        System.out.print(getValueByIndex(i)+"->");
        //标记其已经被访问
        isVisited[i]=true;
        queue.addLast(i);
        //判断连是否为空
        while(!queue.isEmpty()) {
            // 当链表不为空时
            u = (Integer) queue.removeFirst();// 得到队头节点
            w = getFirstNeighbor(u);// 得到节点u的第一个邻接节点
            while (w != -1) {// 如果w存在
                if(!isVisited[w]) {
                    System.out.print(getValueByIndex(w) + "->");
                    isVisited[w]=true;
                    queue.addLast(w);    
                }
                //以u为前驱点，找W后面的下一个邻接点
                w = getNextNeighbor(u, w);
            }
        }
        
        
    }
    
    //深度优先遍历算法
    private void dfs(boolean[] isVisited,int i) {
        //访问该节点，直接输出
        System.out.print(getValueByIndex(i)+"->");
        //标记初始节点被访问
        isVisited[i]=true;
        //找到当前节点i的第一个邻接节点
        int firstNeighbor=getFirstNeighbor(i);
        while(firstNeighbor!=-1) {//如果第一个邻接节点存在
            if(!isVisited[firstNeighbor]) {//如果第一个邻接节点未被访问
                dfs(isVisited, firstNeighbor);//对这个节点进行深度优先遍历
            }else {//找到当前节点的第一个邻接节点的下一个节点
                firstNeighbor=getNextNeighbor(i, firstNeighbor);    
            }
        }    
    }
    //对dfs进行重载，遍历所有的节点，并进行dfs
    public void dfs() {
        //遍历所有的节点，进行dfs
        for (int i = 0; i < getNumOfVertex(); i++) {
            if(!isVisited[i]) {
                dfs(isVisited, i);
            }
        }
    }
    //返回节点的个数
    public int getNumOfVertex() {
        return vertexList.size();
    }
    //显示图对应的矩阵
    public void showGraph() {
        for(int[] link:edges) {
            System.out.println(Arrays.toString(link));
        }
    }
    //返回边的数目
    public int getNumOfEdges() {
        return numOfEdges;
    }
    
    //返回节点i对应的数据
    public String getValueByIndex(int i) {
        return vertexList.get(i);
    }
    //返回v1和v2的权值
    public int getWeight(int v1,int v2) {
        return edges[v1][v2];
    }
    //插入节点
    public void insertVertex(String vertex) {
        vertexList.add(vertex);
    }
    
    //添加边
    /**
     * 
     * @param v1 表示第一个顶点的下标
     * @param v2 表示第二个顶点的下标
     * @param weight 表示是否相连
     */
    public void insertEdge(int v1,int v2,int weight) {
        edges[v1][v2]=weight;
        edges[v2][v1]=weight;
        numOfEdges++;
    }
}

 　　3.5 深度优先与广度优先的比较

　　

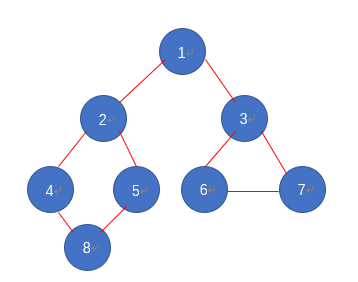
深度优先遍历顺序：1，2，4，8，5，3，6，7

广度优先遍历顺序：1，2，3，4，5，6，7，8