upd on 2021.7.29:
终于在我生日这一天来补这篇博客了,tzc 老鸽子(
前置知识:轮廓线 (dp)
对于有些涉及到相邻格子之间的限制的状压 (dp),如果我们按行转移要枚举 (2^m) 个状态,复杂度过高,但由于我们只需要关心与未转移格子所相邻的格子的状态,因此我们可以考虑逐格转移,那么显然转移的点与未转移的点之间存在一条分界线,我们就称这条线为轮廓线,那么我们只用状压轮廓线以上部分是否选择即可,这样复杂度即可降到 (2^nnm)。
例题:LOJ 2372 -「CEOI2002」臭虫集成电路公司
插头 dp
插头 (dp) 能够用来求解与连通性有关的问题,包括但不限于回路计数、路径问题、连通块最大权值、广义路径问题等,一般对于数据范围极小,并且涉及到与连通性有关的词汇时,可以想到插头 (dp)。
那么就让我们从模板题 P5056 【模板】插头dp 入手来讲解这一神奇的算法(
首先我们需要明白“插头 (dp)”中“插头”的含义是什么,在上面前置知识:轮廓线 (dp) 中我们定义了轮廓线对吧,那么对于一个回路而言,显然这条轮廓线会穿过回路中的某些点,那么我们就把这条轮廓线与回路产生的这些交点称作“插头”,譬如对于下图而言,橙色的轮廓线上方就有四个插头:
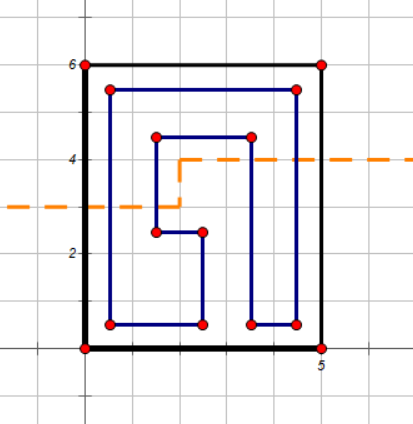
那么我们怎样记录一个插头的状态呢?首先由于轮廓线长度为 (m+1),因此需用一个长度为 (m+1) 的数组来存储这个轮廓线的状态,具体来说假设我们当前遍历到第 (i) 行第 (j) 列,那么我们轮廓线第 (x(x<j)) 位存储第 (x) 列分界线上下插头的状态,第 (j+1) 位存储第 (i) 行第 (j) 列与第 (i) 行第 (j+1) 列分界线之间插头的状态,第 (y(y>j+1)) 位存储第 (y-1) 列分界线上下插头的状态。但是记录插头时候,仅仅简单地记录一个点是否存在插头是不可行的,因为对于上面例子中的图和下图,它们轮廓线上有无插头的状态一致,但转移的情况却不同:
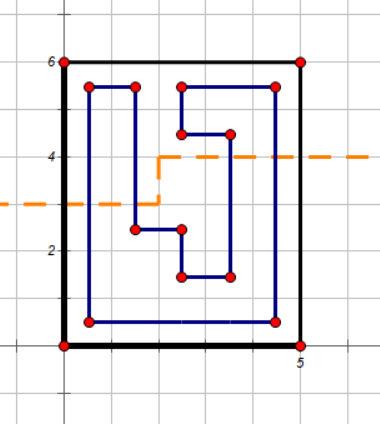
因此我们不仅要记录每个点是否存在插头,还要记录哪些插头在同一个连通块中,此时就有两种思路:
-
最小表示法,也就是将所有联通块看作一个不同的数,并且对于每个连通块,记其编号为第一个属于这个连通块的点前面不同连通块的个数加一,即序列 ((2,4,3,3,5,2,1)) 按照这种方式可以被重新标号为 ((1,2,3,3,4,1,5)),上面例子中的第一幅(靠上的图)轮廓线的状态可以被标号为 ((1,2,0,0,2,1)),下面一幅图轮廓线的状态可以被标号为 ((1,1,0,0,2,2))
-
括号表示法,注意到对于回路而言,显然不会存在交叉的情况,因此对于任意连通块,必须恰好有两个点属于这个连通块,并且如果将这两个点视作一个区间,那么这些连通块表示的区间只存在包含、外离,不存在相交的情况,此时我们的维护方法就呼之欲出:括号序列!具体来说,对于所有连通块第一次出现的位置,我们将其看作左括号,第二次出现的位置也就自然看成右括号,那么此时得到的括号序列显然是合法的括号序列。那么有人就问了,没有插头怎么办呢?对于没有插头的地方我们直接给它补上 0 即可,譬如上面的情况用括号序列表示就是 (((00))),下面的情况用括号序列表示就是 (()00())。
注意:只有回路、路径才能用括号表示法,对于连通块,由于不存在上述性质,因此只能用最小表示法!
那么怎么运用插头 (dp) 解决上述问题呢?考虑状压 (dp),(dp_{i,j,S}) 表示考了到了第 (i) 行第 (j) 列,当前轮廓线上状态为 (S) 的方案数。这里咱们采用括号表示法,即将左括号视作 (1),右括号视作 (2),看成一个四进制数(为什么是四进制呢,因为可以用位运算减少常数),转移就分情况讨论:
- ((i,j)) 上有障碍,此时该点上显然不能连接插头,因此只有 (j) 和 (j+1) 处都没有插头的情况才可以转移,并且状态不变。
- ((i,j)) 上没有障碍,那么记 (b1) 为 (S) 第 (j) 位的值,(b2) 为 (S) 第 (j+1) 位的值。
- 如果 (b1=0) 且 (b2=0),那么只能在 ((i,j)) 处新建两个插头,即将 (S) 的第 (j) 位改为 (1),第 (j+1) 位改为 (2)。
- 如果 (b1 e 0) 且 (b2=0),那么这个插头可以直行,也可以右拐,直行的情况就是将插头从第 (j) 位移至第 (j+1) 位,右拐的情况就是插头位置保持不变,分别转移一下即可。
- 如果 (b1=0) 且 (b2 e 0),同上
- 如果 (b1=1) 且 (b2=1),那么我们显然只能将这两个插头合并起来并去掉它们,但是直接去掉相当于在括号序列中去掉两个左括号,会导致括号序列的不合法,因此我们需要向右找到与第二个左括号匹配的右括号,将其改为左括号。
- 如果 (b1=2) 且 (b2=2),与第四种情况类似,不过这次我们要找到与第一个右括号匹配的左括号并将其改为右括号。
- 如果 (b1=2) 且 (b2=1),那直接把这个插头删除即可。
- 如果 (b1=1) 且 (b2=2),那么闭合这个插头就会形成闭合回路,对于此题而言,由于只能形成一个闭合回路,因此该情况只能在 (i=ex) 且 (j=ey) 的情况下转移,其中 ((ex,ey)) 为最右下角的空格子。
还有一个细节,就是我们 DP 的时候四进制数的值域可能很大,高达 (2^{24}),直接枚举会爆,不过注意到可以成为合法的括号序列的状态数量并不算多,因此考虑剪枝。考虑对 DP 建一个哈希表,具体来说,由于轮廓线 DP 是可以用滚动数组优化的,因此考虑从 (dp_{i,j,S}) 转移到 (dp_{i,j+1,T}) 时就将 (T) 插入哈希表,如果发现哈希表中这个值已经存在了就将贡献累加上去,查询所有有用的 DP 就遍历一遍哈希表即可,具体实现细节可见代码。
冷知识:(10^5) 级别的哈希表模数:(65537,123457,333337,333667,786433)
const int MAXN=12;
const int MOD=123457;
const int MAX=3e6;
int n,m,pw4[MAXN+3],ex,ey;char s[MAXN+3][MAXN+3];
int hd[MOD+3],nxt[MAX+5],key[2][MAX+5],cnt[2],cur=0,pre=1;
ll val[2][MAX+5],ans=0;
void insert(int x,ll v){
for(int e=hd[x%MOD];e;e=nxt[e])
if(key[cur][e]==x) return val[cur][e]+=v,void();
nxt[++cnt[cur]]=hd[x%MOD];hd[x%MOD]=cnt[cur];
key[cur][cnt[cur]]=x;val[cur][cnt[cur]]=v;
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) scanf("%s",s[i]+1);
for(int i=1;i<=n;i++) for(int j=1;j<=m;j++)
if(s[i][j]=='.') ex=i,ey=j;
for(int i=(pw4[0]=1);i<=MAXN;i++) pw4[i]=pw4[i-1]<<2;
cnt[cur]=1;val[cur][1]=1;
for(int i=1;i<=n;i++){
for(int j=1;j<=cnt[cur];j++) key[cur][j]<<=2;
for(int j=1;j<=m;j++){
memset(hd,0,sizeof(hd));cur^=pre^=cur^=pre;cnt[cur]=0;
for(int k=1;k<=cnt[pre];k++){
int msk=key[pre][k];ll cnt=val[pre][k];
// printf("%d %d %d %lld
",i,j,msk,cnt);
int b1=msk>>(j-1<<1)&3,b2=msk>>(j<<1)&3;
if(s[i][j]=='*'){
if(!b1&&!b2) insert(msk,cnt);
} else{
if(!b1&&!b2){
if(s[i][j+1]=='.'&&s[i+1][j]=='.')
insert(msk+pw4[j-1]+2*pw4[j],cnt);
} else if(!b1&&b2){
if(s[i][j+1]=='.') insert(msk,cnt);
if(s[i+1][j]=='.') insert(msk-pw4[j]*b2+pw4[j-1]*b2,cnt);
} else if(b1&&!b2){
if(s[i+1][j]=='.') insert(msk,cnt);
if(s[i][j+1]=='.') insert(msk-pw4[j-1]*b1+pw4[j]*b1,cnt);
} else if(b1==1&&b2==1){
int c=1;
for(int l=j+1;l<=m;l++){
if(msk>>(l<<1)&1) ++c;
if(msk>>(l<<1|1)&1) --c;
if(!c){
insert(msk-pw4[j-1]-pw4[j]-pw4[l],cnt);
break;
}
}
} else if(b1==2&&b2==2){
int c=1;
for(int l=j-2;~l;l--){
if(msk>>(l<<1)&1) --c;
if(msk>>(l<<1|1)&1) ++c;
if(!c){
insert(msk-2*pw4[j-1]-2*pw4[j]+pw4[l],cnt);
break;
}
}
} else if(b1==2&&b2==1){
insert(msk-2*pw4[j-1]-pw4[j],cnt);
} else {
if(i==ex&&j==ey) ans+=cnt;
}
}
}
}
} printf("%lld
",ans);
return 0;
}
例题就暂(yong)时(yuan)咕掉了。