





题解:
第一题:二分, 因为配对是肯定的,距离递增;这道题我用的斜率,他没有卡精度,所以可以用三角形算乘法更优
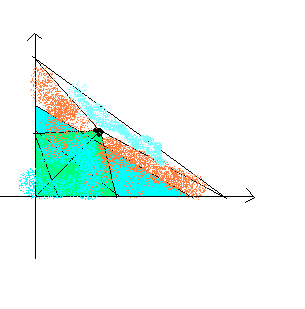
若P在某条线外面,则他与线端点形成的三角形>线形成的三角形, 否则为小于;
条件是 Y[i] * Xp + X[i] * Yp >= X[i]*Y[i];

#include <bits/stdc++.h> #define ll long long using namespace std; const int M = 1e5 +10; double x[M], y[M], k[M]; double x1, yy, k1; bool check(int t){ double x2 = y[t]/(k1 - k[t]); double y2 = k1*x2; if(x2 <= x1 && y2 <= yy)return 1; return 0; } int main() { freopen("geometry.in","r",stdin); freopen("geometry.out","w",stdout); int n, m; scanf("%d", &n); for(int i = 1; i <= n; i++)scanf("%lf", &x[i]); for(int i = 1; i <= n; i++)scanf("%lf", &y[i]); sort(x+1, x+1+n); sort(y+1, y+1+n); for(int i = 1; i <= n; i++) k[i] = -y[i]/x[i]; scanf("%d", &m); while(m--){ scanf("%lf%lf", &x1, &yy); k1 = yy/x1; int lf = 1, rg = n, ans = 0; while(lf <= rg){ int mid = (lf + rg) >> 1; if(check(mid))ans = mid, lf = mid + 1; else rg = mid - 1; } printf("%d ", ans); } return 0; }
第二题:dp, dp[u]表示U到根的最小距离, 且在U点买票;
最开始想的是某个点有选和不选, dp[u][1] = dp[u可以到达的地方][1/0] dp[u][0] = ??? (0 buy, 1 not buy);
就不会转移了;

#include <bits/stdc++.h> const int M = 1e5 + 10, P = 20, inf = 2e9; using namespace std; int mi[M], h[M], dp[M], anc[M][P+1], ch[M][P+1], tot; void read(int &x){ x=0;int f=1;char c=getchar(); while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();} while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();} x*=f; } struct node{int k, w;}; struct edge{int v,nxt;}G[M]; void add(int u, int v){G[++tot].nxt = h[u]; h[u] = tot; G[tot].v = v; } vector <node> vec[M]; void dfs(int u, int f){ dp[u] = inf; anc[u][0] = f; ch[u][0] = dp[f]; for(int i = 1; i <= P; i++)ch[u][i] = inf; for(int i = 1; i <= P; i++) anc[u][i] = anc[anc[u][i-1]][i-1]; for(int i = 1; i <= P; i++) ch[u][i] = min(ch[anc[u][i-1]][i-1], ch[u][i-1]); if(u == 1)dp[u] = 0; else { int siz = vec[u].size(), i; for(i = 0; i < siz; i++){ int dis = vec[u][i].k; int j = P, now = u, tmp = inf; while(now && dis){ while(mi[j] > dis && j >= 0)j--; dis -= mi[j]; tmp = min(tmp, ch[now][j]); now = anc[now][j]; } dp[u] = min(dp[u], tmp + vec[u][i].w); } } for(int i = h[u]; i; i = G[i].nxt){ int v = G[i].v; dfs(v, u); } } int main() { freopen("party.in","r",stdin); freopen("party.out","w",stdout); mi[0] = 1; //for(int i = 0; i <= P; i++)ch[0][i] = inf; int n, m, q; read(n), read(m); for(int i = 1; i < M; i++)mi[i] = mi[i-1]*2; for(int i = 1; i < n; i++){ int u, v; read(u), read(v); add(v, u); } for(int i = 1; i <= m; i++){ int v, k, w; read(v), read(k), read(w); vec[v].push_back((node){k, w}); } dfs(1, 0); //for(int i = 1; i <= n; i++)printf("%d ", dp[i]); read(q); while(q--){ int x; read(x); printf("%d ", dp[x]); } return 0; }
第三题:带区间的splay, 又是zjj同学帮我看出来的,万分感谢啊~~ 细节地方还要仔细思考,尤其是鼠标的操作
还有 字符数组不能swap之类的骚气操作, 字符串不可以减

#include <bits/stdc++.h> using namespace std; string s; const int M = 5 * 1e6; int len, root, p[2], tot=1; char s1[M]; struct Splay{ int fa[M], lazy[M], ch[M][2], siz[M]; char val[M]; inline void up(int x){ siz[x] = siz[ch[x][0]] + siz[ch[x][1]]+ 1; } inline void down(int x){ if(!lazy[x])return; swap(ch[x][0], ch[x][1]); lazy[ch[x][0]]^=1; lazy[ch[x][1]]^=1; lazy[x] = 0; } int build(int f,int x, int l = 1, int r = len+2){ if(l > r)return 0; int mid = (l + r) >> 1; fa[x] = f; val[x] = s1[mid]; ch[x][0] = build(x,++tot, l, mid-1); ch[x][1] = build(x,++tot, mid+1, r); up(x); return x; } void rotate(int x, int d){ int y = fa[x]; down(y);down(x); ch[y][d^1] = ch[x][d]; if(ch[x][d]) fa[ch[x][d]] = y; fa[x] = fa[y]; if(fa[y]) ch[fa[y]][y == ch[fa[y]][1]] = x; ch[x][d] = y, fa[y] = x; up(y); up(x); } void splay(int x, int targt = 0){ while(fa[x] != targt){ int y = fa[x]; if(x == ch[y][0]){ if(y == ch[fa[y]][0] && fa[y] != targt) rotate(y, 1); rotate(x, 1); } else{ if(y == ch[fa[y]][1] && fa[y] != targt) rotate(y, 0); rotate(x, 0); } } if(!targt)root = x; } void print(int now){ if(!now)return; down(now); print(ch[now][0]); if(val[now] >= 33 && val[now] <= 126)printf("%c", val[now]); //cout<<now<<" "<<val[now]<<endl; print(ch[now][1]); } int find(int x){ int now = root; while(1){ if(!now)return 0; down(now); int t = siz[ch[now][0]]; if(x <= t)now = ch[now][0]; else if(x >= t + 2){ x -= (t+1); now = ch[now][1]; } else return now; } } void insert(int pos, char v){ int ln = find(pos - 1), rn = find(pos); splay(ln); splay(rn, ln); ch[rn][0] = ++tot; //cout<<val[ln]<<endl; siz[tot] = 1; val[tot] = v; fa[tot] = rn; up(rn);up(ln); } void del(int pos){ int ln = find(pos), rn = find(pos + 2); splay(ln); splay(rn, ln); ch[rn][0] = 0; up(rn);up(ln); } void rev(int lf, int rg){ int ln = find(lf), rn = find(rg); splay(ln); splay(rn, ln); int pp = ch[rn][0]; lazy[pp]^=1; up(rn);up(ln); } }Tr; inline int dir(){ getchar(); return getchar( ) == 'L' ? 0 : 1; } void Lmove(){ int t = dir(); if(p[t] == 1){puts("F");return;} puts("T"); p[t]--; } void Rmove(){ int t = dir(); if(p[t] == len+1){puts("F");return;} puts("T"); p[t]++; } void Insert(){ int t = dir();getchar(); char val = getchar(); Tr.insert(p[t]+1, val); len++; if(p[t^1] >= p[t])p[t^1]++; p[t]++;puts("T"); } void Del(){ int t = dir(); if(p[t] == len+1){puts("F");return;} puts("T"); if(p[t^1] > p[t]) p[t^1]--; len--; Tr.del(p[t]); } void Rev(){ if(p[0] >= p[1]){puts("F");return;} Tr.rev(p[0], p[1]+1); puts("T"); } void print(){ Tr.print(root); printf(" "); } int main() { freopen("editor.in","r",stdin); freopen("editor.out","w",stdout); cin>>s; char rp=3; len = s.size(); s1[1]=rp; s1[tot]=rp; for (int i = 2; i <= len + 1; i++) { s1[i]=s[i-2]; } root = Tr.build(0,1); int n; scanf("%d", &n); p[0] = 1; p[1] = len+1; while(n--) { char opt, gb, zm; scanf(" %c", &opt); switch(opt){ case 'S':{print();break;} case '<':{Lmove();break;} case '>':{Rmove();break;} case 'I':{Insert();break;} case 'D':{Del();break;} case 'R':{Rev();break;} } //print(); // cout<<p[0]<<" "<<p[1]<<" "<<len<<endl; } return 0; }
