引言:
之前去西安某游戏公司面试前端开发岗位,考了我一道赛马题,当场没想出来,面试也就顺理成章的凉凉。
回家之后,我仔细研究了一下,结合网络上的一些思路,梳理出来一个目前个人认为的最优解,但不知道会不会存在更少的情况。
本文就结合这道题目,分享一下我个人解此题的一个详细思路,用图文的形式去呈现。
题目要求:
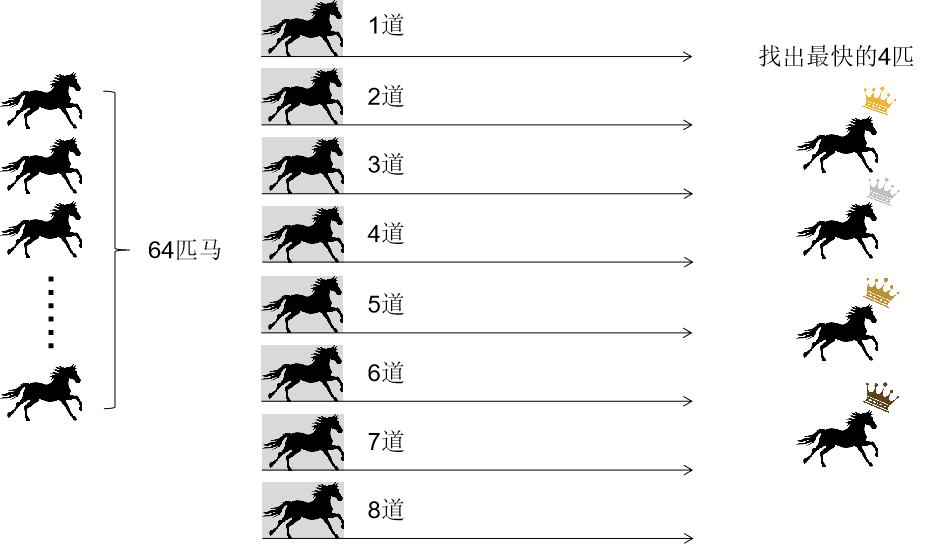
现有64匹马,赛场上有8条跑道(一场最多赛8匹)。问,在不用计时器的情况下,最少情况下,赛多少场能够找到最快的4匹。如图:
分析:
根据题意,我们可以很轻松想到,64匹马能够排成8*8的方阵(一共8组,每组8匹)。
刚好每组8匹刚好占满8个跑道,不构成浪费。
无论怎样,至少每匹马都得参加比赛,有参考依据,才有可能得出结论。
1.第一步:(8场)
如上述分析,将64匹马随机分成8组,每组8匹,让它们跑去吧。
这样我们至少可以得出每一组的排名,这里为了不混淆,组统一用ABCDEFGH表示,名次用12345678表示。
现在我们知道每一组的排名,但不能轻易下结论。极端情况下,A组的8匹有可能是最快的8匹,B组的第1也许很快,但比起A组第8,仍然是难以望其项背。
这样我们还不能确定具体名次,我们可以让每一组的第1名加赛一场,得出每组按第一升序排列的矩阵。
2.第二步:(1场)
如上述,每组第1加赛一场。我们可以按名次排列出一个8*8的矩阵。
如下表所示,A为第1名所在组,B为第2名所在组,以此类推。
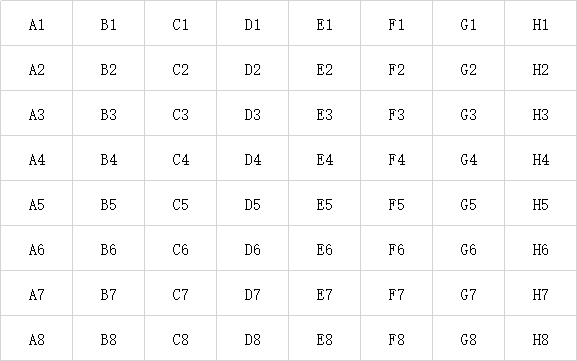
这样下来,A1一定是64匹中的大哥,最快的那匹,我们用土豪金标注。(因为是每组第1中的第1)
而且,E1作为每组第1中的第5,已经不可能在整体前4了,因为A1,B1,C1,D1都比它快,所以EFGH组全部淘汰。(用白色标注)
对于D1而言,是每组第1中的第4,是可能入围的,而且最好名次也是第4,那么D2~D8作为D1的小弟肯定没戏了。
同理,对C1而言,最好名次也是第3,C2作为C1小弟可以勉强争一下第4,所以C3~C8淘汰。
那么B4~B8以及A5~A8全部淘汰,现在场上只剩下了A1~A4,B1~B3,C1~C2,D1。总共10匹马。用红色标记。如图:

3.第三步:(1场,最多2场)
还剩下10匹马,但我们已知A1一定是全场最佳,所以剩下9匹马需要再比一场。
现在只有8个赛道,却有9匹马,看样子是需要让其中一匹马在场下看热闹了。
而这匹马最好选择“边缘人”,也就是在淘汰边缘的,相比较而言D1的位置最为尴尬,ABC组里边的非第1,随时有可能挤掉它成功上位。
所以,选择D1看热闹是最合适不过的了。(因为D1最多拿第4,否则淘汰)
接下来,我们就让A2,A3,A4,B1,B2,B3,C1,C2去跑。
跑完之后,这样我们可以参照C1的名次来判断接下来需要怎么赛。
若C1是本组第4~7名,则整体2~4名和本组前3一一对应,加上A1的第1名,构成前4。(结束)
若C1是本组第3名,则让C2和D1加赛一场,抢第4名。(加赛一场,结束)
若C1是本组第2名,则前4就是A1,C1,C2及D1,C2和D1不必进行季军争夺,怎么争夺都是一个第3一个第4。(结束)
4.第四步:(总结)
结合上述分析,看C1最后一场如果不跑第3就是最少情况,最少需要10场,(8+1+1)。
这仅仅是目前本人认为最少的场次,如果有更犀利的思路,我会积极采纳!