Codeforces Round#435 DIV.2

Codeforces Round#435 DIV.2

手动翻译的中文题面链接 https://www.luogu.org/contest/show?tid=3503  题面在这里就不粘了

原链接http://codeforces.com/contest/862/

#435A.Bahmoud and Ehab and the MEX

代码超短，不解释了↓

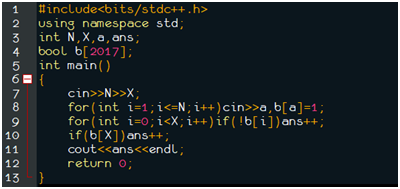
#435B.Bahmoud and Ehab and the bipartiteness

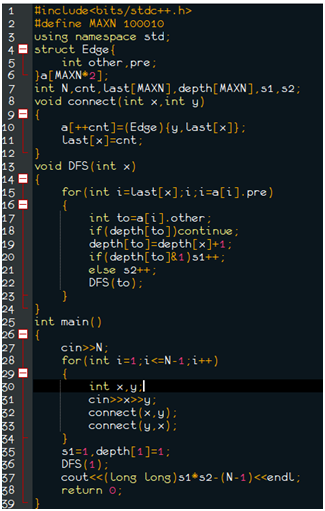
题看着挺玄乎，题意差不多是给你一个二分图，让你把能连的边连上，就是把同色点的数量拿DFS求出来之后乘法原理

而且这个二分图是一个树，一层一个颜色，十分好算，记得开long long，还有要减去N-1 (原先存在的边数)

#435C.Lahmoud and Ehab and the xor

玄学异或 我们知道 a^b^(a^b) 肯定是0的这就很好了

总体方向就是搞出n-1个数疑惑起来等于，再加上一个x就可以了

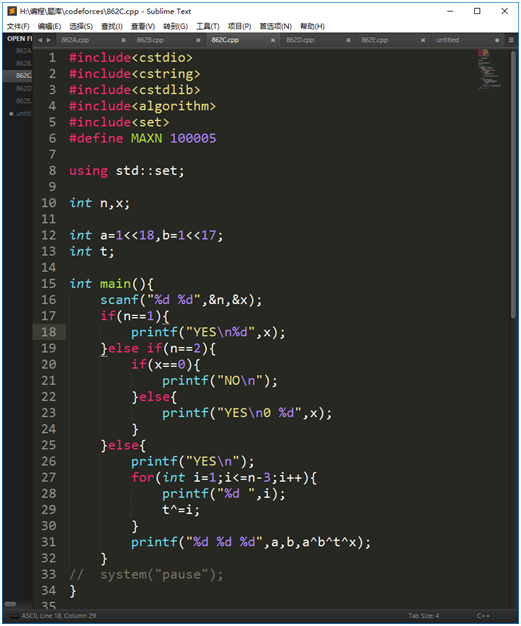
先随意取m个数异或在一起（简单的选了1~m） 记异或和为t 那么我们理论上只要再加上一个t 一个x 共m+2个数就可以解决

然而t x 可能就在那m个数中 那就出现重复了 所以要给他俩一人一个buff 也就是异或上一个1~m中不可能出现的数 这里选了（1<<18）和（1<<19）因为他们都大于1e5不可能出现在1~m中 然后问题就解决了 数分别为1......m, (1<<18)^(1<<19), (1<<18)^t, (1<<19)^x 也就得到m=n-3

对于n<3 的情况特判就行了 注意唯一的不可能情况就是x=0 n=2

#435D.Mahmoud and Ehab and the binary string

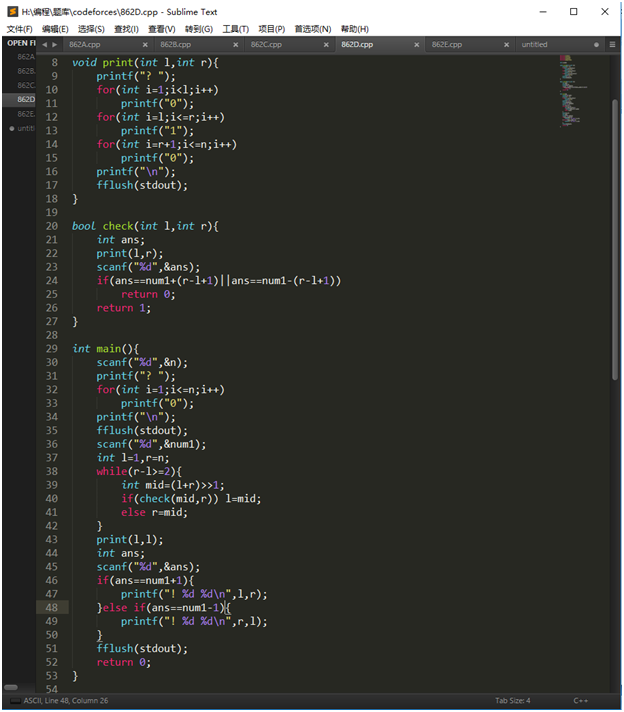
根据题意一定存在连续的01或者10 而你只要找到他的位置就行了 我们可以二分的找判断查找区间内是不是0 1都有

先询问全为0的串 查出1的个数num1 接下来每个查询区间 都询问只把区间置1的串 如果回答与num1的差值等于区间长度 那么就说明这个区间内全是1或0 那么查询失败 直到最后l与r差小于2时（找到了01或10） 判断一下是01还是10就可以输出答案了

 

#435E.Mahmoud and Ehab and the function

有一个长度为N的数组a和长度为M的数组b，定义一个函数f(j)，(0<=j<=m-n)，引入一个c[i]=a[i]-b[i+j]，f(j)=|c1-c2+c3-c4……cN|

Q次询问 给数组a的区间 [l,r]加上 x，求f[j]的最小值。

看起来可能有点麻烦，

仔细观察，可以发现，a数组在f[j]的每个j值里都是不变的，b数组在整个过程中是没有修改的。

于是预处理出所有 b的j~j+N的区间和 排个序， 每次只修改a，在查询时二分查b的最优值即可。

注意：计算前缀和注意奇偶和正负的关系 ( <-主要问题,计算修改什么的都看奇偶)，别搞乱，其他小细节看代码。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll a[100005],b[100005],c[100005],sum;
int n,m,k;
ll fabs(ll x){return x>0ll?x:-x;}
void query(){
    int p=lower_bound(c+1,c+1+m-n+1,-sum)-c;   　　　　 //因为是求和的绝对值最小，所以查与-sum最接近的b区间和
    if(p==1) printf("%I64d
",fabs(sum+c[1]));
    else if(p==n-m+2) printf("%I64d
",fabs(sum+c[n-m+1]));
    else printf("%I64d
",min(fabs(sum+c[p]),fabs(sum+c[p-1])));　　//好懂吧
}
int main()
{
    scanf("%d%d%d",&n,&m,&k);
    for(int i=1;i<=n;++i) scanf("%I64d",a+i);
    for(int i=1;i<=n;++i)
        if(i&1)sum+=a[i];
        else sum-=a[i];　　　　　　　　　　　　　　　　　　  //算数组a的和，奇加偶减
    for(int i=1;i<=m;++i) scanf("%I64d",b+i);
    for(int i=1;i<=n;++i)　　　　　　　　　　　　　　　　　　//计算b所有的j-j+N区间和，注意正负
        if(i&1) c[1]-=b[i]; else c[1]+=b[i];
    for(int i=2;i<=m-n+1;++i)
        if(n&1) c[i]=-c[i-1]-b[i-1]-b[i+n-1]; 
        else c[i]=-c[i-1]-b[i-1]+b[i+n-1];
    sort(c+1,c+1+m-n+1);
    query();
    for(int i=1;i<=k;++i){
        ll x,y,z;scanf("%I64d%I64d%I64d",&x,&y,&z);
        if((y-x+1)&1) if(x&1)sum+=z;else sum-=z;　　 　　//数组a的总和修改
        query();
    }
    return 0;
} 

#435F.Mahmoud and Ehab and the final stage

数据结构题，笛卡尔树，还不会 =、=

dalao可以去水一下，题面：

有N个字符串s1,s2……sN，接下来Q次操作，形式为

·1 a b(1<=a<=b<=N) ，查询： 当a<=l<=r<=b,求出(r-l+1)*LCP(sl,sl+1,……,sr-1,sr)的最大值，LCP是最长公共前缀的长度。

·2 x y ，修改 ： x是整数，y是字符串，把第x个字符串改成y