树链剖分

普通树链剖分

• 修改点x到点y路径上各点的值
• 查询点x到点y路径上各点的值
• 修改点x子树各点的值
• 查询点x子树上各点的值

问题1：树上差分

问题2：LCA(dis[u] + dis[v] - 2 * dis[LCA(u,v)])

但是同时完成的话区间复杂度会很大。回想以前线段树就是同时完成前缀和与差分的，那么只需要用线段树去完成即可。

但是线段树是对于一段连续的区间的。但我们可以想到，利用(LCA(u,v))思想把[u,v]区间拆成两段，然后合并一下就可以了。另外就是对于线段树的叶子结点，需要对应树上的dfs序值即可

定义：

名称	含义
son[u]	u的重儿子的编号
top[u]	u所在的链的深度最小的结点编号
depth[u]	u的深度
fa[u]	u的父亲结点
dfn[u]	u的DFS序
rk[u]	dfs序为u的结点在树中所对应的结点的权值
siz[u]	以u为根的子树的结点个数

概念	含义
重儿子	父亲结点的所有儿子中子树结点数最多的结点
轻儿子	父亲结点中除了重儿子以外的儿子结点
重边	父亲结点和重儿子连成的边
轻边	父亲结点和轻儿子连成的边
重链	由多条重边连接而成的路径
轻链	由多条轻边连接而成的路径

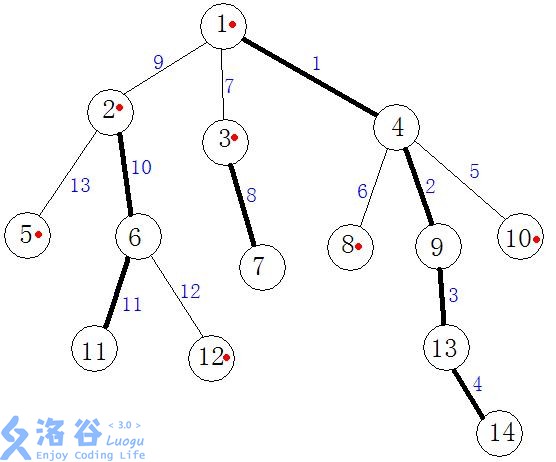
黑线是重边，红点是轻点，也是每条链的top

预处理1

标记每个节点的父亲，深度，大小，重儿子

void dfs1(int now,int fa){
    fa[now] = fa; depth[now] = depth[fa] + 1;
    size[now] = 1;
    for(int i = head[now]; i; i = e[i].next){
        int v = e[i].to;
        if(v != fa){
            dfs1(v, now);
            size[now] += size[v];
            if(size[v] > size[son[now]])son[now] = v;
        }
    }
}

预处理2

标记dfs序,top和rk

轻点的top就是本事，用于赋初始值

void dfs2(int u,int rt){
    dfn[u] = ++cnt;
    rk[cnt] = a[u];
    top[u] = rt;
    if(son[u])dfs2(son[u],rt);
    for(int i = head[u]; i; i = e[i].next){//对其他轻点赋值
        int v = e[i].to;
        if(v != fa[u] && v != son[u])dfs2(v,v);
    }
}

构建线段树

要求区间加，区间查询

因为是建立了dfs序，所以线段树的叶子结点应该对于在dfs序下的值，即rk[i]

struct Tree{
    int l,r;
    int sum,lazy;
    #define l(p) tree[p].l
    #define r(p) tree[p].r
    #define sum(p) tree[p].sum
    #define lazy(p) tree[p].lazy
    #define lson(p) p << 1
    #define rson(p) p << 1 | 1
}tree[N << 2];
void pushup(int p){
    sum(p) = (sum(lson(p)) + sum(rson(p))) % mod;
}
void pushdown(int p){
    if(lazy(p)){
        sum(lson(p)) = (sum(lson(p)) + lazy(p) * (r(lson(p)) - l(lson(p)) + 1)) % mod;
        sum(rson(p)) = (sum(rson(p)) + lazy(p) * (r(rson(p)) - l(rson(p)) + 1)) % mod;
        lazy(lson(p)) = (lazy(lson(p)) + lazy(p)) % mod;
        lazy(rson(p)) = (lazy(rson(p)) + lazy(p)) % mod;
        lazy(p) = 0;
    }
}
void build(int p,int l,int r){
    l(p) = l,r(p) = r,lazy(p) = sum(p) = 0;
    if(l == r){
        sum(p) = rk[l] % mod;
        return ;
    }
    int mid = (l + r) >> 1;
    build(lson(p),l,mid);
    build(rson(p),mid + 1,r);
    pushup(p);
}
void change(int p,int l,int r,int x){//区间加x
    if(l <= l(p) && r(p) <= r){
        sum(p) = (sum(p) + x * (r(p) - l(p) + 1) % mod) % mod;
        lazy(p) = (lazy(p) + x) % mod;
        return;
    }
    pushdown(p);
    int mid = (l(p) + r(p)) >> 1;
    if(l <= mid)change(lson(p),l,r,x);
    if(r > mid)change(rson(p),l,r,x);
    pushup(p);
}
ll Query(int p,int l,int r){
    if(l <= l(p) && r(p) <= r)return sum(p);
    pushdown(p);
    ll ans = 0;
    int mid = (l(p) + r(p)) >> 1;
    if(l <= mid)ans = (ans + Query(lson(p),l,r)) % mod;
    if(r > mid)ans = (ans + Query(rson(p),l,r)) % mod;
    return ans;
}

树上修改与查询

相当于把[u,v]分成了两段

如果查询的是([u,v])，那么我们可以把它分成([u,LCA(u,,v)],[v,LCA(u,v)])两个区间，但是这样会有重，所以对于轻点，就是每条链的祖先点，把一个区间分成两个链即可

void ModifyOnTree(int u,int v,int val){
    while(top[u] != top[v]){
        if(depth[top[u]] < depth[top[v]])swap(u,v);
        change(1,dfn[top[u]],dfn[u],val);
        u = fa[top[u]];
    }
    if(depth[u] > depth[v])swap(u,v);
    change(1,dfn[u],dfn[v],val);
}
ll QueryOnTree(int u,int v){
    ll ans = 0;
    while(top[u] != top[v]){
        if(depth[top[u]] < depth[top[v]])swap(u,v);
        ans += Query(1,dfn[top[u]],dfn[u]);
        u = fa[top[u]];
    }
    if(depth[u] > depth[v])swap(u,v);
    ans = (ans + Query(1,dfn[u],dfn[v])) % mod;
    return ans;
}

子树修改与查询

因为dfs序是连续的，所以对于u的子树，dfs序必定是([dfn[u],dfn[u] + size[u] - 1])

void ModifyOnSon(int u,int v){
    change(1,dfn[u],dfn[u] + siz[u] - 1,v);
}
ll QueryOnSon(int u){
    return Query(1,dfn[u],dfn[u] + siz[u] - 1);
}

模板

• 修改点x到点y路径上各点的值
• 查询点x到点y路径上各点的值
• 修改点x子树各点的值
• 查询点x子树上各点的值

#include <iostream>
#include <cstdio>
#define ll long long
using namespace std;
const int N = 1e5 + 5;
int dfn[N], cnt, son[N], top[N], depth[N], fa[N], siz[N], rk[N];
int head[N], tot, a[N];
int mod;
struct Node{
    int to,next;
}e[N << 1];
void add(int u,int v){
    e[++tot].to = v;
    e[tot].next = head[u];
    head[u] = tot;
}
void dfs1(int now,int fath){
    fa[now] = fath,depth[now] = depth[fath] + 1;
    siz[now] = 1;
    for(int i = head[now]; i; i = e[i].next){
        int v = e[i].to;
        if(v != fath){
            dfs1(v,now);
            siz[now] += siz[v]; 
            if(siz[v] > siz[son[now]])son[now] = v;
        }
    }
}
void dfs2(int u,int rt){
    dfn[u] = ++cnt;
    rk[cnt] = a[u];
    top[u] = rt;
    if(son[u])dfs2(son[u],rt);
    for(int i = head[u]; i; i = e[i].next){
        int v = e[i].to;
        if(v != fa[u] && v != son[u])dfs2(v,v);
    }
}
struct Tree{
    int l,r;
    int sum,lazy;
    #define l(p) tree[p].l
    #define r(p) tree[p].r
    #define sum(p) tree[p].sum
    #define lazy(p) tree[p].lazy
    #define lson(p) p << 1
    #define rson(p) p << 1 | 1
}tree[N << 2];
void pushup(int p){
    sum(p) = (sum(lson(p)) + sum(rson(p))) % mod;
}
void pushdown(int p){
    if(lazy(p)){
        sum(lson(p)) = (sum(lson(p)) + lazy(p) * (r(lson(p)) - l(lson(p)) + 1)) % mod;
        sum(rson(p)) = (sum(rson(p)) + lazy(p) * (r(rson(p)) - l(rson(p)) + 1)) % mod;
        lazy(lson(p)) = (lazy(lson(p)) + lazy(p)) % mod;
        lazy(rson(p)) = (lazy(rson(p)) + lazy(p)) % mod;
        lazy(p) = 0;
    }
}
void build(int p,int l,int r){
    l(p) = l,r(p) = r,lazy(p) = sum(p) = 0;
    if(l == r){
        sum(p) = rk[l] % mod;
        return ;
    }
    int mid = (l + r) >> 1;
    build(lson(p),l,mid);
    build(rson(p),mid + 1,r);
    pushup(p);
}
void change(int p,int l,int r,int x){//区间加x
    if(l <= l(p) && r(p) <= r){
        sum(p) = (sum(p) + x * (r(p) - l(p) + 1) % mod) % mod;
        lazy(p) = (lazy(p) + x) % mod;
        return;
    }
    pushdown(p);
    int mid = (l(p) + r(p)) >> 1;
    if(l <= mid)change(lson(p),l,r,x);
    if(r > mid)change(rson(p),l,r,x);
    pushup(p);
}
ll Query(int p,int l,int r){
    if(l <= l(p) && r(p) <= r)return sum(p);
    pushdown(p);
    ll ans = 0;
    int mid = (l(p) + r(p)) >> 1;
    if(l <= mid)ans = (ans + Query(lson(p),l,r)) % mod;
    if(r > mid)ans = (ans + Query(rson(p),l,r)) % mod;
    return ans;
}
void ModifyOnTree(int u,int v,int val){
    while(top[u] != top[v]){
        if(depth[top[u]] < depth[top[v]])swap(u,v);
        change(1,dfn[top[u]],dfn[u],val);
        u = fa[top[u]];
    }
    if(depth[u] > depth[v])swap(u,v);
    change(1,dfn[u],dfn[v],val);
}
ll QueryOnTree(int u,int v){
    ll ans = 0;
    while(top[u] != top[v]){
        if(depth[top[u]] < depth[top[v]])swap(u,v);
        ans += Query(1,dfn[top[u]],dfn[u]);
        u = fa[top[u]];
    }
    if(depth[u] > depth[v])swap(u,v);
    ans = (ans + Query(1,dfn[u],dfn[v])) % mod;
    return ans;
}
void ModifyOnSon(int u,int v){
    change(1,dfn[u],dfn[u] + siz[u] - 1,v);
}
ll QueryOnSon(int u){
    return Query(1,dfn[u],dfn[u] + siz[u] - 1);
}
int main(){
    int n,m,root;scanf("%d%d%d%d",&n,&m,&root,&mod);
    for(int i = 1; i <= n; i++)scanf("%d",&a[i]);
    for(int i = 1; i < n; i++){
        int u,v;scanf("%d%d",&u,&v);
        add(u,v);add(v,u);
    }
    dfs1(root,0);
    dfs2(root,root);
    build(1,1,n);
    while(m--){
        int op;scanf("%d",&op);
        if(op == 1){
            int x,y,z;scanf("%d%d%d",&x,&y,&z);
            ModifyOnTree(x,y,z);
        }else if(op == 2){
            int x,y;scanf("%d%d",&x,&y);
            printf("%lld
", QueryOnTree(x,y));
        }else if(op == 3){
            int x,z;scanf("%d%d",&x,&z);
            ModifyOnSon(x,z);
        }else if(op == 4){
            int x;scanf("%d",&x);
            printf("%lld
", QueryOnSon(x));
        }
    }
    return 0;
}

题

传送门

• 单点修改
• 区间查询
• 区间最大值
  轻松解决

#include <iostream>
#include <cstdio>
#define ll long long
using namespace std;
const int N = 3e4 + 5;
struct Tree{
    int l,r;
    int sum,maxx;
    #define l(p) tree[p].l
    #define r(p) tree[p].r
    #define sum(p) tree[p].sum
    #define maxx(p) tree[p].maxx
    #define lson(p) p << 1
    #define rson(p) p << 1 | 1
}tree[N << 2];
struct Edge{
    int to,next;
}e[N << 1];
int head[N], tot;
void add(int u,int v){
    e[++tot].to = v;
    e[tot].next = head[u];
    head[u] = tot;
}
int a[N];
int depth[N], fa[N], cnt, dfn[N], rk[N], son[N], siz[N], top[N];
void dfs1(int now,int fath){
    fa[now] = fath,depth[now] = depth[fath] + 1;
    siz[now] = 1;
    for(int i = head[now]; i; i = e[i].next){
        int v = e[i].to;
        if(v != fath){
            dfs1(v,now);
            siz[now] += siz[v]; 
            if(siz[v] > siz[son[now]])son[now] = v;
        }
    }
}
void dfs2(int u,int rt){
    dfn[u] = ++cnt;
    rk[cnt] = a[u];
    top[u] = rt;
    if(son[u])dfs2(son[u],rt);
    for(int i = head[u]; i; i = e[i].next){
        int v = e[i].to;
        if(v != fa[u] && v != son[u])dfs2(v,v);
    }
}
void pushup(int p){
    sum(p) = sum(lson(p)) + sum(rson(p));
    maxx(p) = max(maxx(lson(p)),maxx(rson(p)));
}
void build(int p,int l,int r){
    l(p) = l,r(p) = r;
    if(l == r){
        sum(p) = maxx(p) = rk[l];
        return;
    }
    int mid = (l + r) >> 1;
    build(lson(p),l,mid);
    build(rson(p),mid+1,r);
    pushup(p);
}
void Change(int p,int x,int v){
    if(l(p) == r(p)){
        sum(p) = maxx(p) = v;
        return;
    }
    int mid = (l(p) + r(p)) >> 1;
    if(mid >= x)Change(lson(p),x,v);
    else Change(rson(p),x,v);
    pushup(p);
}
int QuerySum(int p,int l,int r){
    if(l <= l(p) && r(p) <= r)return sum(p);
    int mid = (l(p) + r(p)) >> 1;
    int ans = 0;
    if(l <= mid)ans += QuerySum(lson(p),l,r);
    if(r > mid)ans += QuerySum(rson(p),l,r);
    return ans;
}
int QueryMax(int p,int l,int r){
    if(l <= l(p) && r(p) <= r)return maxx(p);
    int mid = (l(p) + r(p)) >> 1;
    int ans = -30005;
    if(l <= mid)ans = max(ans,QueryMax(lson(p),l,r));
    if(r > mid)ans = max(ans,QueryMax(rson(p),l,r));
    return ans;
}
void ModifyOnTree(int u,int c){
    Change(1,dfn[u],c);
}
int QueryOnTreeSum(int u,int v){
    int ans = 0;
    while(top[u] != top[v]){
        if(depth[top[u]] < depth[top[v]])swap(u,v);
        ans += QuerySum(1,dfn[top[u]],dfn[u]);
        u = fa[top[u]];
    }
    if(depth[u] > depth[v])swap(u,v);
    ans += QuerySum(1,dfn[u],dfn[v]);
    return ans;
}
int QueryOnTreeMax(int u,int v){
    int ans = -30005;
    while(top[u] != top[v]){
        if(depth[top[u]] < depth[top[v]])swap(u,v);
        ans = max(ans,QueryMax(1,dfn[top[u]],dfn[u]));
        u = fa[top[u]];
    }
    if(depth[u] > depth[v])swap(u,v);
    ans = max(ans,QueryMax(1,dfn[u],dfn[v]));
    return ans;
}
int main(){
    int n;scanf("%d",&n);
    for(int i = 1; i < n; i++){
        int u,v;scanf("%d%d",&u,&v);
        add(u,v);add(v,u);
    }
    for(int i = 1; i <= n; i++)scanf("%d",&a[i]);
    dfs1(1,0);dfs2(1,1);
    build(1,1,n);
    int m;scanf("%d",&m);
    while(m--){
        char s[10];scanf("%s",s);
        if(s[0] == 'Q' && s[1] == 'M'){
            int u,v;scanf("%d%d",&u,&v);
            printf("%d
", QueryOnTreeMax(u,v));
        }else if(s[0] == 'C'){
            int x,c;scanf("%d%d",&x,&c);
            ModifyOnTree(x,c);
        }else if(s[0] == 'Q' && s[1] == 'S'){
            int u,v;scanf("%d%d",&u,&v);
            printf("%d
", QueryOnTreeSum(u,v));
        }
    }
    return 0;
}