给定一个整数数组 ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
示例:
**输入:** [-2,1,-3,4,-1,2,1,-5,4],
**输出:** 6
**解释:** 连续子数组 [4,-1,2,1] 的和最大,为 6。
方法一:暴力法
public int MaxsubArray1(int nums[]) {
int Sum = 0, MaxSum = 0;
int N = nums.length; //获得当前数组个数
for(int i = 0; i < N; i++) {
Sum = 0;
for(int j = i; j < N; j++) {
Sum += nums[j];
if(Sum > MaxSum) { //比较子列和,当大于最大项时
MaxSum = Sum;
}
}
}
return MaxSum;
}
复杂度分析:
- 时间复杂度:O(N^2) 遍历两次数组
- 空间复杂度:O(1) 使用常数空间
方法二:动态规划法
public int MaxsubArray2(int nums[]) {
int Sum = 0, MaxSum = 0;
int N = nums.length; //获得当前数组个数
for(int i = 0; i < N; i++) {
sum += nums[i];
if(sum > MaxSum) {
MaxSum = sum;
}else if(sum < 0) {
sum = 0;
}
}
return MaxSum;
}
算法分析:
数组边移动边处理,之前的子序和若为负,继续移动至最右端。
复杂度分析:
- 时间复杂度:O(N)遍历一次数组
- 空间复杂度:O(1)使用常数空间
方法三:分治法
public static int MaxSubArray3 (int nums[]) {
int N = nums.length();
if(N < 1) {
return 0;
}
int left = 0;
int right = N - 1;
return DivideAndConquer(nums, left, right);
}
public static int DivideAndConquer(int nums[], int left, int right) {
//当子序列个数为1时
if(left == right) {
if(nums[left] > 0) {
return nums[left];
}else return 0;
}
//当子序列个数大于1时, 分别求左右子序列和
int mid = (left + right)/2;
int MaxLeftSum = DivideAndConquer(nums, left, mid);
int MaxRightSum = DivideAndConquer(nums, mid, right);
/*求中子序列和(跨分界线)*/
//分界线左边
int MaxLeftBorderSum = 0, int LeftBoderSum = 0;
for(int i = mid; i >= left; i--) {
LeftBoderSum += nums[i];
if(LeftBoderSum > MaxLeftBorderSum) {
MaxLeftBorderSum = LeftBoderSum;
}
}
//分界线右边
int MaxRightBorderSum = 0, int RightBoderSum = 0;
for(int j = mid; j <= right; j++) {
RightBoderSum += nums[j];
if(RightBoderSum > MaxRightBorderSum) {
MaxRightBorderSum = RightBoderSum;
}
}
//中子序列和
int MaxBorderSum = MaxLeftBorderSum + MaxRightBorderSum;
return MaxThree(MaxBorderSum, MaxLeftSum, MaxRightSum);
}
/*找出三数中最大值
*/
public static int MaxThree(int a, int b, int c) {
return a > b ? a > c ? a : c : b > c ? b : c;
}
算法分析:
将问题分解为小问题,再用递归求解。最后合并小问题的解得到问题的解。
假设最大子序列有n个数字,当n==1时,直接返回该数字;当n>1时,分为左子序列和、右子序列和、中子序列和(包括左右子序列的元素)。这里来自leetcode的讨论区的图更好理解:
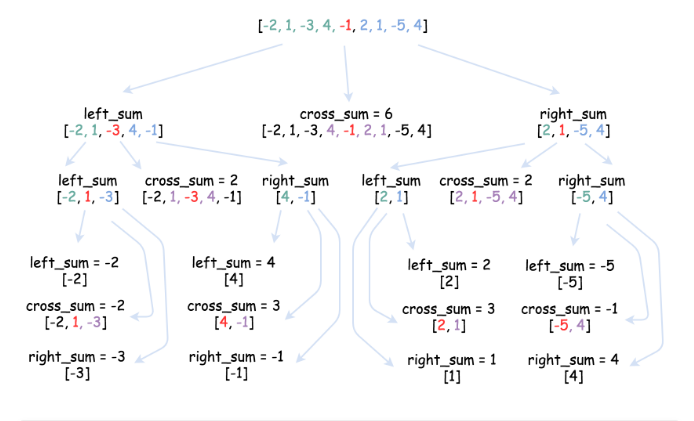
复杂度分析:
- 时间复杂度:O(NlogN)最多需要N次递归
- 空间复杂度:O(logN) 递归树的深度