谁说数学是枯燥的?(给我站出来)在数学里,有很多欢乐而又深刻的数学定理。这些充满生活气息的数学定理,不但深受数学家们的喜爱,在数学迷的圈子里也广为流传
。
喝醉的小鸟
定理:喝醉的酒鬼总能找到回家的路,喝醉的小鸟则可能永远也回不了家。
假设有一条水平直线,从某个位置出发,每次有 50% 的概率向左走1米,有50%的概率向右走1米。按照这种方式无限地随机游走下去,最终能回到出发点的概率是多少?答案是100% 。在一维随机游走过程中,只要时间足够长,我们最终总能回到出发点。
现在考虑一个喝醉的酒鬼,他在街道上随机游走。假设整个城市的街道呈网格状分布,酒鬼每走到一个十字路口,都会概率均等地选择一条路(包括自己来时的那条路)继续走下去。那么他最终能够回到出发点的概率是多少呢?答案也还是 100% 。刚开始,这个醉鬼可能会越走越远,但最后他总能找到回家路。
不过,醉酒的小鸟就没有这么幸运了。假如一只小鸟飞行时,每次都从上、下、左、右、前、后中概率均等地选择一个方向,那么它很有可能永远也回不到 出发点了。事实上,在三维网格中随机游走,最终能回到出发点的概率只有大约 34% 。
这个定理是著名数学家波利亚(George Pólya)在 1921 年证明的。
随着维度的增加,回到出发点的概率将变得越来越低。在四维网格中随机游走,最终能回到出发点的概率是 19.3% ,而在八维空间中,这个概率只有 7.3% 。
“你在这里”
定理:把一张当地的地图平铺在地上,则总能在地图上找到一点,这个点下面的地上的点正好就是它在地图上所表示的位置。
也就是说,如果在商场的地板上画了一张整个商场的地图,那么你总能在地图上精确地作一个“你在这里”的标记。
1912 年,荷兰数学家布劳威尔(Luitzen Brouwer)证明了这么一个定理:
假设 D 是某个圆盘中的点集,f 是一个从 D 到它自身的连续函数,则一定有一个点 x ,使得 f(x) = x 。换句话说,让一个圆盘里的所有点做连续的运动,则总有一个点可以正好回到运动之前的位置。这个定理叫做布劳威尔不动点定理(Brouwer fixed point theorem)。
除了上面的“地图定理”,布劳威尔不动点定理还有很多其他奇妙的推论。如果取两张大小相同的纸,把其中一张纸揉成一团之后放在另一张纸上,根据布劳威尔不动点定理,纸团上一定 存在一点,它正好位于下面那张纸的同一个点的正上方。
这个定理也可以扩展到三维空间中去:当你搅拌完咖啡后,一定能在咖啡中找到一个点,它在搅拌前后的位置相同(虽然这个点在搅拌过程中可 能到过别的地方)。
不能抚平的毛球
定理:你永远不能理顺椰子上的毛。
想象一个表面长满毛的球体,你能把所有的毛全部梳平,不留下任何像鸡冠一样的一撮毛或者像头发一样的旋吗?拓扑学告诉你,这是办不到的。这叫做毛球定理(hairy ball theorem),它也是由布劳威尔首先证明的。用数学语言来说就是,在一个球体表面,不可能存在连续的单位向量场。这个定理可以推广到更高维的空间:对于任意一个偶数维的球面,连续的单位向量场都是不存在的。
毛球定理在气象学上有一个有趣的应用:由于地球表面的风速和风向都是连续的,因此由毛球定理,地球上总会有一个风速为 0 的地方,也就是说气旋和风眼是不可避免的。
气候完全相同的另一端
定理:在任意时刻,地球上总存在对称的两点,他们的温度和大气压的值正好都相同。
波兰数学家乌拉姆(Stanisław Marcin Ulam)曾经猜想,任意给定一个从 n 维球面到 n 维空间的连续函数,总能在球面上找到两个与球心相对称的点,他们的函数值是相同的。
1933 年,波兰数学家博苏克(Karol Borsuk)证明了这个猜想,这就是拓扑学中的博苏克-乌拉姆定理(Borsuk–Ulam theorem)。
博苏克-乌拉姆定理有很多推论,其中一个推论就是,在地球上总存在对称的两点,他们的温度和大气压的值正好都相同(假设地球表面各地的温度差异和大气压差异是连续变化的)。这是因为,我们可以把温度值和大气压值所有可能的组合看成平面直角坐标系上的点,于是地球表面各点的温度和大气压变化情况就可以看作是二维球面到二维平面的函数,由博苏克-乌拉姆定理便可推出,一定存在两个函数值相等的对称点。
当 n = 1 时,博苏克-乌拉姆定理则可以表述为,在任一时刻,地球的赤道上总存在温度相等的两个点。对于这个弱化版的推论,我们有一个非常直观的证明方法:假设赤道上有 A、B 两个人,他们站在关于球心对称的位置上。如果此时他们所在地方的温度相同,问题就已经解决了。下面我们只需要考虑他们所在地点的温度一高一低的情况。不妨假设,A 所在的地方是 10 度,B 所在的地方是 20 度吧。现在,让两人以相同的速度相同的方向沿着赤道旅行,保持两人始终在对称的位置上。假设在此过程中,各地的温度均不变。旅行过程中,两人不断报出自己 当地的温度。等到两人都环行赤道半周后,A 就到了原来 B 的位置,B 也到了 A 刚开始时的位置。在整个旅行过程中,A 所报的温度从 10 开始连续变化(有可能上下波动甚至超出 10 到 20 的范围),最终变成了 20;而 B 经历的温度则从 20 出发,最终连续变化到了 10。那么,他们所报的温度值在中间一定有“相交”的一刻,这样一来我们也就找到了赤道上两个温度相等的对称点。
平分火腿三明治
定理:任意给定一个火腿三明治,总有一刀能把它切开,使得火腿、奶酪和面包片恰好都被分成两等份。
而且更有趣的是,这个定理的名字真的就叫做“火腿三明治定理”(ham sandwich theorem)。它是由数学家亚瑟•斯通(Arthur Stone)和约翰•图基(John Tukey)在 1942 年证明的,在测度论中有着非常重要的意义。
火腿三明治定理可以扩展到 n 维的情况:
如果在 n 维空间中有 n 个物体,那么总存在一个 n - 1 维的超平面,它能把每个物体都分成“体积”相等的两份。这些物体可以是任何形状,还可以是不连通的(比如面包片),甚至可以是一些奇形怪状的点集,只要满足点集可测就行了。
另外,小编再给大家介绍一个最奇妙的数学定理:分球悖论!
巴拿赫-塔斯基悖论,又称分球悖论,是一条经过严格证明的数学定理。
可以描述为:
一个三维实心球,必定存在一种办法分成有限部分,然后仅仅通过旋转和平移,就可以组成两个和原来完全相同的球(半径相同,密度相同……所有性质都相同)。
这是一条非常反常识的数学定理,基于“选择公理”严格地推导出来,而且不容置疑。
这个定理还有更强的版本描述:
一块石头经过分解,可以随意组合成任何东西,可以拼成一个星球,也可以拼成一个人,甚至藏进一个细胞之中!
要理解其中的原理,需要对“无穷”这个概念有深刻的理解,“希尔伯特旅馆”大家可能听过。
这个比喻,是对“无穷”的一个通俗解释,分球悖论也可以通过这个比喻来解释。
我们来类比,“球分成无限份”相当于“旅馆的无限个房间“,把这无限个房间分成偶数和奇数两类,我们再单独把这两类房间分开,分别称为“希尔伯特旅馆一”和“希尔伯特旅馆二”。
如果我们不看序号,或者把两个旅馆的房间重新编号,请问:这两个新的旅馆,和原来的“希尔伯特旅馆”有区别吗?
答案是:没有区别,两个新旅馆,和原来的旅馆一摸一样,房间数一样,每个房间的大小也一样。
分球悖论指出:实心球也存在这样的分解办法,然后进行分类和重组,就能变“一”为“二”;两者本质上是一样的。
有人可能会觉得,新的实心球,质量肯定变为原来的一半!
其实不是的,因为在无穷面前,分球悖论并不满足质量守恒,比如我们假设每个单元的质量为Δm(无穷小),在我们分类的时候,Δm并没有被分解,我们分解的是“∞“。
在数学中,“可数∞”的一半,还是“可数∞”,于是,我们确实得到了两个,和原来一模一样的实心球。
数学上允许这样的事发生,但是为了避免这样的悖论,出现在现实中,大自然把世界设定为离散的,于是有了量子,有了普朗克长度。
所以,实际的事物不可能无限细分,分球悖论也就无法在现实中进行。
或许,这正是数学和大自然,完美统一的表现。
来源:数学中竟然还有这样的定理!
谁说数学是枯燥的?在数学里,有很多欢乐而又深刻的数学定理。这些充满生活气息的数学定理,不但深受数学家们的喜爱,在数学迷的圈子里也广为流传。
喝醉的小鸟
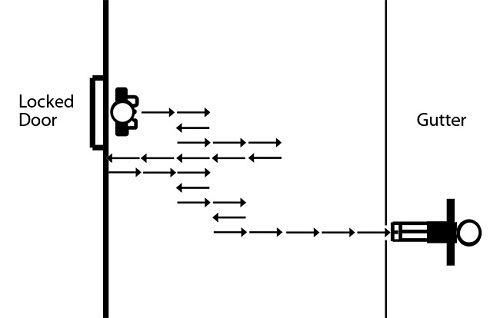
定理:喝醉的酒鬼总能找到回家的路,喝醉的小鸟则可能永远也回不了家。
假设有一条水平直线,从某个位置出发,每次有 50% 的概率向左走1米,有50%的概率向右走1米。按照这种方式无限地随机游走下去,最终能回到出发点的概率是多少?答案是100% 。在一维随机游走过程中,只要时间足够长,我们最终总能回到出发点。
现在考虑一个喝醉的酒鬼,他在街道上随机游走。假设整个城市的街道呈网格状分布,酒鬼每走到一个十字路口,都会概率均等地选择一条路(包括自己来时的那条路)继续走下去。那么他最终能够回到出发点的概率是多少呢?答案也还是 100% 。刚开始,这个醉鬼可能会越走越远,但最后他总能找到回家路。
不过,醉酒的小鸟就没有这么幸运了。假如一只小鸟飞行时,每次都从上、下、左、右、前、后中概率均等地选择一个方向,那么它很有可能永远也回不到 出发点了。事实上,在三维网格中随机游走,最终能回到出发点的概率只有大约 34% 。
这个定理是著名数学家波利亚(George Pólya)在 1921 年证明的。随着维度的增加,回到出发点的概率将变得越来越低。在四维网格中随机游走,最终能回到出发点的概率是 19.3% ,而在八维空间中,这个概率只有 7.3% 。
“你在这里”

定理:把一张当地的地图平铺在地上,则总能在地图上找到一点,这个点下面的地上的点正好就是它在地图上所表示的位置。
也就是说,如果在商场的地板上画了一张整个商场的地图,那么你总能在地图上精确地作一个“你在这里”的标记。
1912 年,荷兰数学家布劳威尔(Luitzen Brouwer)证明了这么一个定理:假设 D 是某个圆盘中的点集,f 是一个从 D 到它自身的连续函数,则一定有一个点 x ,使得 f(x) = x 。换句话说,让一个圆盘里的所有点做连续的运动,则总有一个点可以正好回到运动之前的位置。这个定理叫做布劳威尔不动点定理(Brouwer fixed point theorem)。
除了上面的“地图定理”,布劳威尔不动点定理还有很多其他奇妙的推论。如果取两张大小相同的纸,把其中一张纸揉成一团之后放在另一张纸上,根据布劳威尔不动点定理,纸团上一定 存在一点,它正好位于下面那张纸的同一个点的正上方。
这个定理也可以扩展到三维空间中去:当你搅拌完咖啡后,一定能在咖啡中找到一个点,它在搅拌前后的位置相同(虽然这个点在搅拌过程中可 能到过别的地方)。
不能抚平的毛球

定理:你永远不能理顺椰子上的毛。
想象一个表面长满毛的球体,你能把所有的毛全部梳平,不留下任何像鸡冠一样的一撮毛或者像头发一样的旋吗?拓扑学告诉你,这是办不到的。这叫做毛球定理(hairy ball theorem),它也是由布劳威尔首先证明的。用数学语言来说就是,在一个球体表面,不可能存在连续的单位向量场。这个定理可以推广到更高维的空间:对于任意一个偶数维的球面,连续的单位向量场都是不存在的。
毛球定理在气象学上有一个有趣的应用:由于地球表面的风速和风向都是连续的,因此由毛球定理,地球上总会有一个风速为 0 的地方,也就是说气旋和风眼是不可避免的。
气候完全相同的另一端

定理:在任意时刻,地球上总存在对称的两点,他们的温度和大气压的值正好都相同。
波兰数学家乌拉姆(Stanisław Marcin Ulam)曾经猜想,任意给定一个从 n 维球面到 n 维空间的连续函数,总能在球面上找到两个与球心相对称的点,他们的函数值是相同的。1933 年,波兰数学家博苏克(Karol Borsuk)证明了这个猜想,这就是拓扑学中的博苏克-乌拉姆定理(Borsuk–Ulam theorem)。
博苏克-乌拉姆定理有很多推论,其中一个推论就是,在地球上总存在对称的两点,他们的温度和大气压的值正好都相同(假设地球表面各地的温度差异和大气压差异是连续变化的)。这是因为,我们可以把温度值和大气压值所有可能的组合看成平面直角坐标系上的点,于是地球表面各点的温度和大气压变化情况就可以看作是二维球面到二维平面的函数,由博苏克-乌拉姆定理便可推出,一定存在两个函数值相等的对称点。
当 n = 1 时,博苏克-乌拉姆定理则可以表述为,在任一时刻,地球的赤道上总存在温度相等的两个点。对于这个弱化版的推论,我们有一个非常直观的证明方法:假设赤道上有 A、B 两个人,他们站在关于球心对称的位置上。如果此时他们所在地方的温度相同,问题就已经解决了。下面我们只需要考虑他们所在地点的温度一高一低的情况。不妨假设,A 所在的地方是 10 度,B 所在的地方是 20 度吧。现在,让两人以相同的速度相同的方向沿着赤道旅行,保持两人始终在对称的位置上。假设在此过程中,各地的温度均不变。旅行过程中,两人不断报出自己 当地的温度。等到两人都环行赤道半周后,A 就到了原来 B 的位置,B 也到了 A 刚开始时的位置。在整个旅行过程中,A 所报的温度从 10 开始连续变化(有可能上下波动甚至超出 10 到 20 的范围),最终变成了 20;而 B 经历的温度则从 20 出发,最终连续变化到了 10。那么,他们所报的温度值在中间一定有“相交”的一刻,这样一来我们也就找到了赤道上两个温度相等的对称点。
平分火腿三明治

定理:任意给定一个火腿三明治,总有一刀能把它切开,使得火腿、奶酪和面包片恰好都被分成两等份。
而且更有趣的是,这个定理的名字真的就叫做“火腿三明治定理”(ham sandwich theorem)。它是由数学家亚瑟•斯通(Arthur Stone)和约翰•图基(John Tukey)在 1942 年证明的,在测度论中有着非常重要的意义。
火腿三明治定理可以扩展到 n 维的情况:如果在 n 维空间中有 n 个物体,那么总存在一个 n - 1 维的超平面,它能把每个物体都分成“体积”相等的两份。这些物体可以是任何形状,还可以是不连通的(比如面包片),甚至可以是一些奇形怪状的点集,只要满足点集可测就行了。
作者:matrix67
链接:https://www.guokr.com/article/53059/
来源:果壳
本文版权属于果壳网(guokr.com),禁止转载。如有需要,请联系sns@guokr.com
Cramer悖论:线性代数的萌芽
在准备前一篇日志时,我查阅了很多经典的悖论。我发现,虽说数学悖论大多是一些让人越想越糊涂的逻辑思维游戏,但也有不少悖论来自于实实在在的数学问题。在缺乏现代数学工具的年代,这些反直觉的结论和看似不可调和的矛盾让数学家们百思不得其解,那些最难解决的悖论甚至为数学新分支的开创带来了足够的动机。不太为人熟知的 Cramer 悖论就是一个漂亮的例子。
这阵子去听田野研究员的代数数论,他说给本科生讲的第一节线性代数是关于克拉默悖论的,觉得挺有意思,便找到了Matrix67的这篇论文。
在描述 Cramer 悖论之前,让我们先来考虑一个简单的情况。两条直线交于一点。反过来,过一点可以做两条不同的直线。事实上,过一点可以做无数条直线。确定一条直线需要两个点才够。一切都很正常。
现在,考虑平面上的两条三次曲线。由于将两个二元三次方程联立求解,最多可以得到 9 组不同的解,因此两条三次曲线最多有 9 个交点。另外,三次曲线的一般形式为
x^3 + a·x^2·y + b·x·y^2 + c·y^3 + d·x^2 + e·x·y + f·y^2 + g·x + h·y + i = 0
这里面一共有 9 个未知系数。代入曲线上的 9 组不同的 (x, y) ,我们就能得出 9 个方程,解出这 9 个未知系数,恢复出这个三次曲线的原貌。也就是说,平面上的 9 个点唯一地确定了一个三次曲线。这次貌似就出问题了: “两条三次曲线交于 9 个点” 和 “ 9 个点唯一地确定一条三次曲线” 怎么可能同时成立呢?既然这 9 个点是两条三次曲线所共有的,那它们究竟会“唯一地”确定出哪条曲线呢?在没有线性代数的年代,这是一个令人匪夷所思的问题。
Cramer 和 Euler 是同一时代的两位大数学家。他们曾就代数曲线问题有过不少信件交流。上面这个问题就是 1744 年 9 月 30 日 Cramer 在给 Euler 的信中提出来的。在信中, Cramer 摆出了两个稍作思考便能看出显然成立的事实:一条三次曲线能用 9 个点唯一地确定下来,两条三次曲线可能产生出 9 个交点。 Cramer 向 Euler 提出了自己的疑问:这两个结论怎么可能同时成立呢?
Euler 心中的疑问不比 Cramer 的少。接下来的几年里,他都在寻找这个矛盾产生的源头。 1748 年, Euler 发表了一篇题为 Sur une contradiction apparente dans la doctrine des lignes courbes (关于曲线规律中的一个明显的矛盾)的文章,尝试着解决这一难题。正如大家所想,矛盾的源头就是, 9 个点不见得能唯一地确定出三次曲线的方程,因为不是每个点的位置都能给我们带来足够的信息。
Euler 试图向人们解释这样一件事情:曲线上的 9 个点虽然给出了 9 个不同的方程,但有时它们并不能唯一地解出那 9 个未知数,因为有些方程是废的。在没有线性代数的年代,解释这件事情并不容易。 Euler 举了一个最简单的例子:方程组
3x − 2y = 5
4y = 6x − 10
表面上存在唯一解,但事实上两个方程的本质相同——第一个方程乘以 2 再移项后就直接变成第二个方程了。换句话说,后一个方程并没有给我们带来新的信息,有它没它都一样。当然,这只是一个最为简单的例子。在当时,真正让人大开眼界的则是 Euler 文中给出的三元一次方程组:
2x − 3y + 5z = 8
3x − 5y + 7z = 9
x − y + 3z = 7
这个方程组也没有唯一解,原因就很隐蔽了:后两个方程之和其实是第一个方程的两倍,换句话说第一个方程本来就能由另外两个方程推出来。因此,整个方程组本质上只有两个不同的方程,它们不足以确定出三个未知数来。 Euler 还给出了一个四元一次方程组的例子,向人们展示了更加复杂的情况。
类似地, 9 个九元一次方程当然也会因为出现重复信息而不存在唯一解,不过具体情况几乎无法预料:很可能方程 (1) 就是方程 (2) 和方程 (5) 的差的多少多少倍,也有可能方程 (7) 和 (9) 的差恰是前三个方程的和。究竟什么叫做一个方程“提供了新的信息”,用什么来衡量一个方程组里的信息量,怎样的方程组才会有唯一解? Euler 承认,“要想给出一个一般情况下的公式是很困难的”。
此时大家或许能体会到, Euler 提出的这些遗留问题太具启发性了,当时的数学研究者们看到之后必然是浑身血液沸腾。包括 Cramer 在内的数学家们沿着 Euler 的思路继续想下去,一个强大的数学新工具——线性代数——逐渐开始成型。没错,这个 Cramer 正是后来提出线性代数一大基本定理—— Cramer 法则——的那个人。
参考资料:
http://en.wikipedia.org/wiki/Cramer’s_paradox
http://www.maa.org/editorial/euler/How Euler Did It 10 Cramers Paradox.PDF