NOIP考点系统过滤 E

目录

1. 图论【搜索】【树】【图的联通】【二分图】【欧拉图】【拓扑序】【计算几何】待更... ...
2. 技巧与思想
3. String
4. DP
5. 数论
6. 数据结构
7. 博弈论
8. 其他

 

---

一、图论

1.搜索

①双向bfs

②dfs

③记忆化

• 一般说来，动态规划总要遍历所有的状态，而搜索可以排除一些无效状态。

• 更重要的是搜索还可以剪枝，可能剪去大量不必要的状态，因此在空间开销上往往比动态规划要低很多。
  记忆化算法在求解的时候还是按着自顶向下的顺序，但是每求解一个状态，就将它的解保存下来，
  以后再次遇到这个状态的时候，就不必重新求解了。
  这种方法综合了搜索和动态规划两方面的优点，因而还是很有实用价值的。

• 搜索相对于动态规划最大的劣势无非就是重复计算子结构，所以我们在搜索的过程中，对于每一个子结构只计算一次，之后保存到数组里，以后要用到的时候直接调用就可以了，这就是记忆化搜索。

• 记忆化搜索=搜索的形式+动态规划的思想

• http://blog.csdn.net/urecvbnkuhbh_54245df/article/details/5847876

• 可以用记忆化搜索计算状态转移方程。不必事先确定各状态的计算顺序，但需要记录每个状态 “是否已经计算过”。 ———刘汝佳《算法竞赛入门经典》

④迭代加深

• http://blog.csdn.net/u014800748/article/details/44998693
• http://blog.csdn.net/logo_fc/article/details/64541202

 

2.树

①树的重心和直径

　　树的重心

　树的重心也叫树的质心。对于一棵树n个节点的无根树，找到一个点，使得把树变成以该点为根的有根树时，最大子树的结点树最小。

　换句话说，删除这个点后最大连通块（一定是树）的结点数最小。

• http://blog.csdn.net/u013076044/article/details/45915745（树的重心的性质以及具体实现代码）

 

　　树的直径（树上最长路）

• http://www.cnblogs.com/wuyiqi/archive/2012/04/08/2437424.html（树的直径的详细证明）
• http://www.cnblogs.com/wuyiqi/archive/2012/03/10/2388501.html（实现代码）

②dfs序

• http://blog.csdn.net/qq_24489717/article/details/50569644（详解）

③树链剖分

• http://blog.sina.com.cn/s/blog_6974c8b20100zc61.html

④LCA（http://www.cnblogs.com/JVxie/p/4854719.html）

在一棵没有环的树上，每个节点肯定有其父亲节点和祖先节点，而最近公共祖先，就是两个节点在这棵树上深度最大的公共的祖先节点。

换句话说，就是两个点在这棵树上距离最近的公共祖先节点。

所以LCA主要是用来处理当两个点仅有唯一一条确定的最短路径时的路径。

• 常用的求LCA的算法有：Tarjan/DFS+ST/倍增 （后两个算法都是在线算法，也很相似，时间复杂度在O(logn)~O(nlogn)之间，较难理解吧~）
• 有的题目可以用线段树来做，代码量很大，时间复杂度也偏高，在O(n)~O(nlogn)之间，优点在于简单粗暴

• Tarjan算法（离线）：
  • 在一次遍历中把所有询问一次性解决，所以其时间复杂度是O(n+q)。优点在于相对稳定，时间复杂度也比较居中，也很容易理解
  • 基本思路：

　　　　　　1.任选一个点为根节点，从根节点开始。

 

　　　　　　2.遍历该点u所有子节点v，并标记这些子节点v已被访问过。

　　　　　　3.若是v还有子节点，返回2，否则下一步。

　　　　　　4.合并v到u上。

　　　　　　5.寻找与当前点u有询问关系的点v。

　　　　　　6.若是v已经被访问过了，则可以确认u和v的最近公共祖先为v被合并到的父亲节点a。

　　　　　　遍历的话需要用到dfs来遍历(我相信来看的人都懂吧...)，至于合并，最优化的方式就是利用并查集来合并两个节点。

⑤Prufer编码和Cayley定理

•  http://www.matrix67.com/blog/archives/682

⑥Prim堆优化 [ O(nlogn) ]、Kruskal [ O(mlogm) ]

• 两者区别

1. PRIM是稠密图用的。KRUSKAL是稀疏图用的。
2. prim针对点，kruskal针对边。一般都是推荐kruskal加路径压缩的启发式合并的并查集，prim加堆优化也不错，只是代码长了点（stl另当别论）
3. 由于Kruskal里面需要用到排序，所以，时间复杂度受到了排序的影响。而且，Kruskal算法又是从边出发的，所以，如果边的数量太多的话，必定会影响排序所用的时间。因此，如果边的数量太多的话，最好是用Prim算法。相比较之下，Kruskal算法的代码比Prim稍微短一点。至于稳定性嘛~~~好像没什么区别....

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　——————出自 noip吧 Prim和 Kruskal的区别

• http://www.cnblogs.com/biyeymyhjob/archive/2012/07/30/2615542.html

⑦分治

3、图的联通

强连通分量

有向图强连通分量：在有向图G中，如果两个顶点vi,vj间（vi>vj）有一条从vi到vj的有向路径，同时还有一条从vj到vi的有向路径，则称两个顶点强连通(strongly connected)。如果有向图G的每两个顶点都强连通，称G是一个强连通图。有向图的极大强连通子图，称为强连通分量(strongly connected components)。

•  当 DFN(u) = Low(u) 时，以u为根的搜索子树上所有节点是一个强连通分量。（对于 DFN 和 low 的解释）
• Tarjan算法

4、二分图

　　二分图又称作二部图，是图论中的一种特殊模型。 设G=(V,E)是一个无向图，如果顶点V可分割为两个互不相交的子集(A,B)，并且图中的每条边（i，j）所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B)，则称图G为一个二分图。

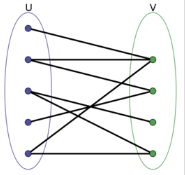
5、欧拉图

欧拉图是指通过图（无向图或有向图）中所有边且每边仅通过一次通路，相应的回路称为欧拉回路。

相关性质：

　　1.无向连通图G是欧拉图，当且仅当G不含奇数度结点(G的所有结点度数为偶数)；

　　2.无向连通图G含有欧拉通路，当且仅当G有零个或两个奇数度的结点；

　　3.有向连通图D是欧拉图，当且仅当该图为连通图且D中每个结点的入度=出度

　　4.有向连通图D含有欧拉通路，当且仅当该图为连通图且D中除两个结点外，其余每个结点的入度=出度，且此两点满足deg－(u)－deg+(v)=±1。（起始点s的入度=出度-1，结束点t的出度=入度-1 或两个点的入度=出度）

　　5.一个非平凡连通图是欧拉图当且仅当它的每条边属于奇数个环。

　　6.如果图G是欧拉图且 H = G - uv，则H有奇数个u,v-迹仅在最后访问v；同时，在这一序列的u,v-迹中，不是路径的迹的条数是偶数。(Todia[1973])　　

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　-----------源自 百度百科

6、拓扑排序

7、计算几何（先忽略这个）

二、技巧与思想

1、二分

2、离散化

• 什么是离散化

3、位运算

4、分块

5、数列差分以及前缀和

6、哈夫曼编码

7、cdq分治

8、启发式合并