Task1
蛤布斯有一个序列,初始为空。它依次将 1-n 插入序列,其中 i 插到当前第 ai 个数的右边 (ai=0 表示插到序列最左边)。它希望你帮 它求出最终序列。
对于 100%的数据,n<=1000000,0<=ai<i。
倒着做,寻找第ai+1个空位插入即可,用线段树维护,注意卡常
O(nlogn)
1 #include<iostream> 2 #include<stdio.h> 3 #include<stdlib.h> 4 #include<string> 5 #include<string.h> 6 #include<algorithm> 7 #include<math.h> 8 #include<queue> 9 #include<set> 10 #include<map> 11 #include<vector> 12 #define re register 13 #define il inline 14 using namespace std; 15 const int N=3000001; 16 int n,a[N],c[N],m=1,ans[N],tot=0; 17 char t[31]; 18 il int read(){ 19 re int hs=0;re char c=getchar(); 20 while(!isdigit(c)) c=getchar(); 21 while(isdigit(c)){ 22 hs=(hs<<3)+(hs<<1)+c-'0'; 23 c=getchar(); 24 } 25 return hs; 26 } 27 il void print(re int h){ 28 tot=0; 29 while(h>0){ 30 t[++tot]=h%10+'0'; 31 h/=10; 32 } 33 for(re int i=tot;i>0;--i) 34 putchar(t[i]); 35 putchar(' '); 36 } 37 int main(){ 38 freopen("sequence.in","r",stdin); 39 freopen("sequence.out","w",stdout); 40 n=read(); 41 while(m<n+2) m<<=1; 42 for(int i=1;i<=n;++i) a[i]=read(),c[i+m]=1; 43 for(int i=m-1;i>0;--i) c[i]=c[i+i]+c[i+i+1]; 44 for(re int i=n,j,k;i>=1;--i){ 45 k=a[i]+1; 46 for(re int p=1;;){ 47 if(c[p+p]>=k){ 48 p<<=1; 49 } 50 else{ 51 k-=c[p+p]; 52 p<<=1;++p; 53 } 54 if(p>m){ 55 j=p-m;break; 56 } 57 } 58 ans[j]=i; 59 for(c[j+=m]=0,j>>=1;j;j>>=1) 60 c[j]=c[j<<1]+c[(j<<1)+1]; 61 } 62 for(int i=1;i<=n;i++) 63 print(ans[i]); 64 return 0; 65 }
Task2
蛤布斯有 n 个物品和一个大小为 m的背包,每个物品有大小和价 值,它希望你帮它求出背包里最多能放下多少价值的物品。
对于 100%的数据,n<=40,0<=m<=10^18,0<=xi,wi<=10^15。
折半枚举,二分查找
O(2^n*n)
1 #include<stdio.h> 2 #include<iostream> 3 #include<stdlib.h> 4 #include<string> 5 #include<string.h> 6 #include<math.h> 7 #include<algorithm> 8 #define il inline 9 #define re register 10 using namespace std; 11 typedef long long ll; 12 const int N=1200010; 13 int n,s,t,l,r,mid; 14 ll W,w[101],v[101],x,y,tot,ans; 15 struct data{ll p,q;} a[N],b[N]; 16 il bool cmp(re data a,re data b){ 17 return (a.p!=b.p)?(a.p<b.p):(a.q>b.q); 18 } 19 int main(){ 20 freopen("pack.in","r",stdin); 21 freopen("pack.out","w",stdout); 22 scanf("%d%I64d",&n,&W); 23 for(int i=1;i<=n;i++) 24 scanf("%I64d%I64d",&w[i],&v[i]); 25 s=n/2;t=n-s; 26 for(re int S=(1<<s)-1;S>0;--S){ 27 x=y=0; 28 for(re int i=0;i<s;++i) 29 if(S&(1<<i)){ 30 x+=w[i+1]; 31 y+=v[i+1]; 32 } 33 a[S].p=x;a[S].q=y; 34 } 35 sort(a+1,a+(1<<s),cmp); 36 for(re int i=1;i<(1<<s);++i){ 37 if(a[i].p>W) break; 38 if(a[i].q>b[tot].q) b[++tot]=a[i]; 39 } 40 b[0].p=b[0].q=0; 41 for(re int S=(1<<t)-1;S>0;--S){ 42 x=y=0; 43 for(re int i=0;i<t;++i) 44 if(S&(1<<i)){ 45 x+=w[i+1+s]; 46 y+=v[i+1+s]; 47 } 48 if(x>W) continue; 49 l=0;r=tot; 50 while(l<r){ 51 mid=(l+r+1)/2; 52 if(b[mid].p<=W-x) l=mid; 53 else r=mid-1; 54 } 55 ans=max(ans,y+b[l].q); 56 } 57 cout<<ans; 58 return 0; 59 }
Task3
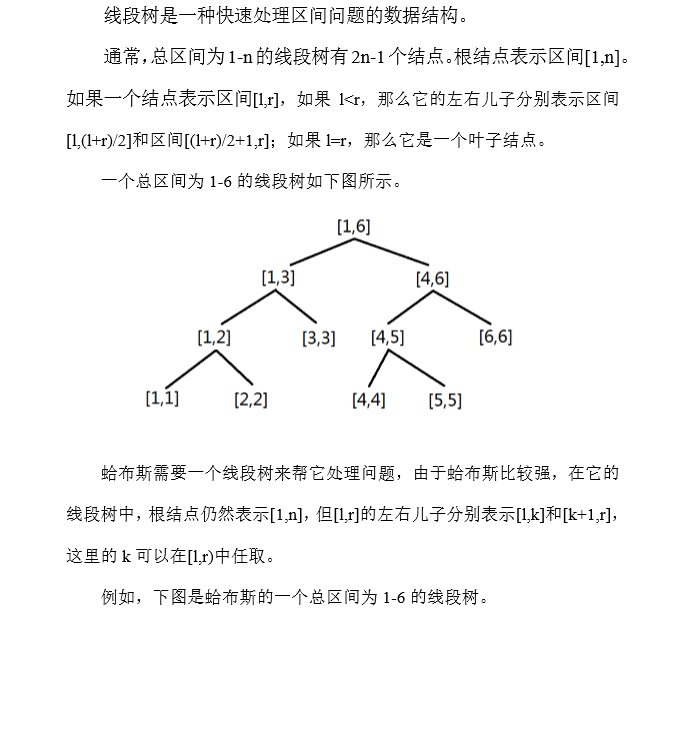
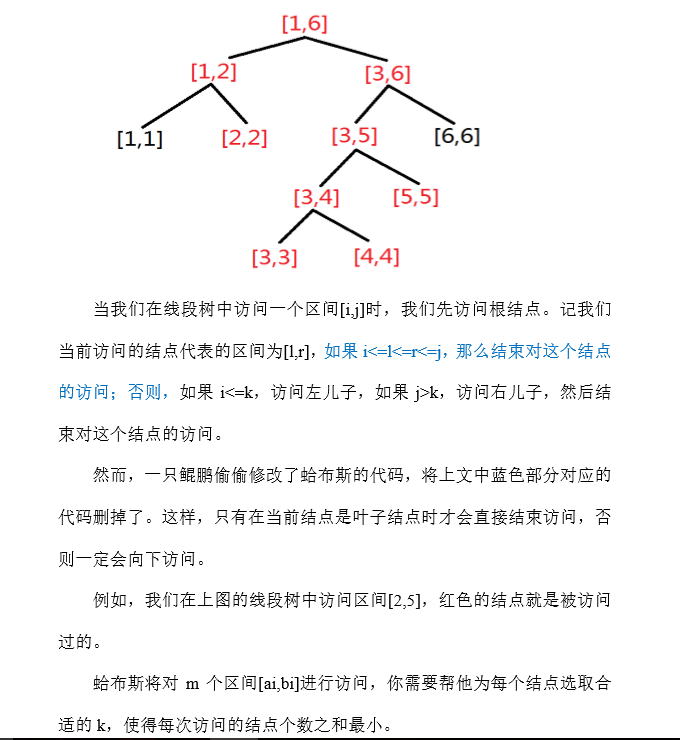
对于 100%的数据,n<=5000,m<=100000
显然如果一条线段树上的线段如果和一个查询有重叠,那么就会被这个查询访问一次。
容易得到暴力动规方程令f[i][j]表示选取区间[i,j]作为线段树上一节点的答案,g[i][j]为[i,j]与多少个查询重叠
f[i][j]=min(f[i][k]+f[k][j]+g[i][j])
显然这满足四边形不等式优化。
时间复杂度O(n^2)