题目描述 Description###
小 B 最近迷上了华容道,可是他总是要花很长的时间才能完成一次。于是,他想到用编程来完成华容道:给定一种局面, 华容道是否根本就无法完成,如果能完成, 最少需要多少时间。
小 B 玩的华容道与经典的华容道游戏略有不同,游戏规则是这样的:在一个 nm 棋盘上有 nm 个格子,其中有且只有一个格子是空白的,其余 nm-1个格子上每个格子上有一个棋子,每个棋子的大小都是 11 的;有些棋子是固定的,有些棋子则是可以移动的;任何与空白的格子相邻(有公共的边)的格子上的棋子都可以移动到空白格子上。游戏的目的是把某个指定位置可以活动的棋子移动到目标位置。给定一个棋盘,游戏可以玩 q 次,当然,每次棋盘上固定的格子是不会变的, 但是棋盘上空白的格子的初始位置、 指定的可移动的棋子的初始位置和目标位置却可能不同。第 i 次玩的时候, 空白的格子在第 EXi 行第 EYi 列,指定的可移动棋子的初始位置为第 SXi 行第 SYi列,目标位置为第 TXi 行第 TYi 列。
假设小 B 每秒钟能进行一次移动棋子的操作,而其他操作的时间都可以忽略不计。请你告诉小 B 每一次游戏所需要的最少时间,或者告诉他不可能完成游戏。
输入描述 Input Description###
第一行有 3 个整数,每两个整数之间用一个空格隔开,依次表示 n、m 和 q;
接下来的 n 行描述一个 n*m 的棋盘,每行有 m 个整数,每两个整数之间用一个空格隔开,每个整数描述棋盘上一个格子的状态,0 表示该格子上的棋子是固定的,1 表示该格子上的棋子可以移动或者该格子是空白的。接下来的 q 行,每行包含 6 个整数依次是 EXi、EYi、SXi、SYi、TXi、TYi,每两个整数之间用一个空格隔开,表示每次游戏空白格子的位置,指定棋子的初始位置和目标位置。
输出描述 Output Description###
输出有 q 行,每行包含 1 个整数,表示每次游戏所需要的最少时间,如果某次游戏无法完成目标则输出−1。
样例输入 Sample Input###
3 4 2
0 1 1 1
0 1 1 0
0 1 0 0
3 2 1 2 2 2
1 2 2 2 3 2
样例输出 Sample Output###
2
-1
数据范围及提示 Data Size & Hint###
【输入输出样例说明】
棋盘上划叉的格子是固定的,红色格子是目标位置,圆圈表示棋子,其中绿色圆圈表示目标棋子。
第一次游戏,空白格子的初始位置是 (3, 2)(图中空白所示),游戏的目标是将初始位置在(1, 2)上的棋子(图中绿色圆圈所代表的棋子)移动到目标位置(2, 2)(图中红色的格子)上。
移动过程如下:
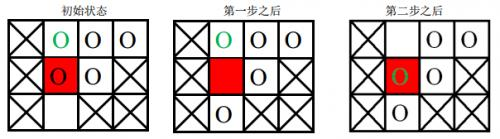
第二次游戏,空白格子的初始位置是(1, 2)(图中空白所示),游戏的目标是将初始位置在(2, 2)上的棋子(图中绿色圆圈所示)移动到目标位置 (3, 2)上。
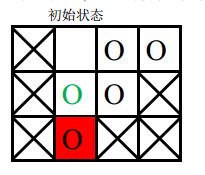
要将指定块移入目标位置,必须先将空白块移入目标位置,空白块要移动到目标位置,必然是从位置(2, 2)上与当前图中目标位置上的棋子交换位置,之后能与空白块交换位置的只有当前图中目标位置上的那个棋子,因此目标棋子永远无法走到它的目标位置, 游戏无法完成。
【数据范围】
对于 30%的数据,1 ≤ n, m ≤ 10,q = 1;
对于 60%的数据,1 ≤ n, m ≤ 30,q ≤ 10;
对于 100%的数据,1 ≤ n, m ≤ 30,q ≤ 500。
之前的一些废话###
深夜了。
题解###
看到题思考了1分钟决定上无脑大BFS,其中(dis(i,j,k,l))表示空白格子在((i,j))目标格子在((k,l))的最少步数。于是说干就干了。30分钟后70分到手,得分效率是不是贼高!
至于正解的话。
代码###
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<cstdio>
#include<queue>
#include<cstdlib>
using namespace std;
typedef long long LL;
#define mem(a,b) memset(a,b,sizeof(a))
typedef pair<int,int> PII;
typedef pair<PII,PII> PPP;
#define X first
#define Y second
#define MP make_pair
inline int read()
{
int x=0,f=1;char c=getchar();
while(!isdigit(c)){if(c=='-')f=-1;c=getchar();}
while(isdigit(c)){x=x*10+c-'0';c=getchar();}
return x*f;
}
const int maxn=35;
int n,m,pic[maxn][maxn],q,dis[maxn][maxn][maxn][maxn],dx[4]={1,0,-1,0},dy[4]={0,1,0,-1};
bool vis[maxn][maxn][maxn][maxn];
PII empty,s,t;
queue <PPP> Q;
bool illegal(int X,int Y){return X<0 || X>=n || Y<0 || Y>=m || !pic[X][Y];}
void solve()
{
mem(dis,42);mem(vis,0);
while(Q.size())Q.pop();
int ans=100000;
empty.X=read()-1;empty.Y=read()-1;
s.X=read()-1;s.Y=read()-1;
t.X=read()-1;t.Y=read()-1;
dis[empty.X][empty.Y][s.X][s.Y]=0;
vis[empty.X][empty.Y][s.X][s.Y]=1;
Q.push(MP(MP(empty.X,empty.Y),MP(s.X,s.Y)));
if(s.X==t.X && s.Y==t.Y){printf("0
");return;}
while(Q.size())
{
PPP now=Q.front();Q.pop();
for(int i=0;i<4;i++)
{
int nx=now.X.X+dx[i],ny=now.X.Y+dy[i];
if(illegal(nx,ny))continue;
if(nx==now.Y.X && ny==now.Y.Y)
{
if(vis[nx][ny][now.X.X][now.X.Y])continue;
dis[nx][ny][now.X.X][now.X.Y]=dis[now.X.X][now.X.Y][now.Y.X][now.Y.Y]+1;
vis[nx][ny][now.X.X][now.X.Y]=1;
Q.push(MP(MP(nx,ny),MP(now.X.X,now.X.Y)));
if(t.X==now.X.X && t.Y==now.X.Y)ans=min(ans,dis[nx][ny][now.X.X][now.X.Y]);
}
else
{
if(vis[nx][ny][now.Y.X][now.Y.Y])continue;
dis[nx][ny][now.Y.X][now.Y.Y]=dis[now.X.X][now.X.Y][now.Y.X][now.Y.Y]+1;
vis[nx][ny][now.Y.X][now.Y.Y]=1;
Q.push(MP(MP(nx,ny),MP(now.Y.X,now.Y.Y)));
if(t.X==now.Y.X && t.Y==now.Y.Y)ans=min(ans,dis[nx][ny][now.Y.X][now.Y.Y]);
}
}
}
printf("%d
", ans!=100000 ? ans : -1);
return;
}
int main()
{
n=read();m=read();q=read();
for(int i=0;i<n;i++)for(int j=0;j<m;j++)pic[i][j]=read();
while(q--)solve();
return 0;
}
总结###
极其热爱这种暴力好写并且得分得的又多的题