A.特别行动队

n<=1000000
看了数据范围和题目感觉就像是斜率优化,然后瞎推了一波式子,没想到A了。
sij表示i+1到j的权值和。
j比k优秀 $$fj+a*sij^{2}+b*sij+c>fk+a*sik^{2}+b*sik+c$$
然后乱整理$$2*a*si<frac{fj-fk}{sj-sk}+a*(sj+sk)-b$$
si递增,维护上凸。
#include<iostream> #include<cstdio> #define ll long long #define ld long double #define MN 1000000 using namespace std; inline int read() { int x = 0 , f = 1; char ch = getchar(); while(ch < '0' || ch > '9'){ if(ch == '-') f = -1; ch = getchar();} while(ch >= '0' && ch <= '9'){x = x * 10 + ch - '0';ch = getchar();} return x * f; } ll f[MN+5],s[MN+5],a,b,c; int top=0,tail=0,q[MN+5]; int n; ll calc(ll x){return a*x*x+b*x+c;} ld solve(int x,int y) { return (ld)(f[x]-f[y])/(s[x]-s[y])+(ld)a*(s[x]+s[y])-(ld)b; } void ins(int x) { while(top>tail&&solve(x,q[top])>solve(q[top],q[top-1])) top--; q[++top]=x; } int get(ll x) { while(top>tail&&solve(q[tail+1],q[tail])>x) tail++; return q[tail]; } int main() { n=read();a=read();b=read();c=read(); for(int i=1;i<=n;i++) s[i]=s[i-1]+read(); for(int i=1;i<=n;i++) { int from=get(1LL*2*a*s[i]); f[i]=f[from]+calc(s[i]-s[from]); ins(i); } cout<<f[n]; return 0; }
B.巡逻
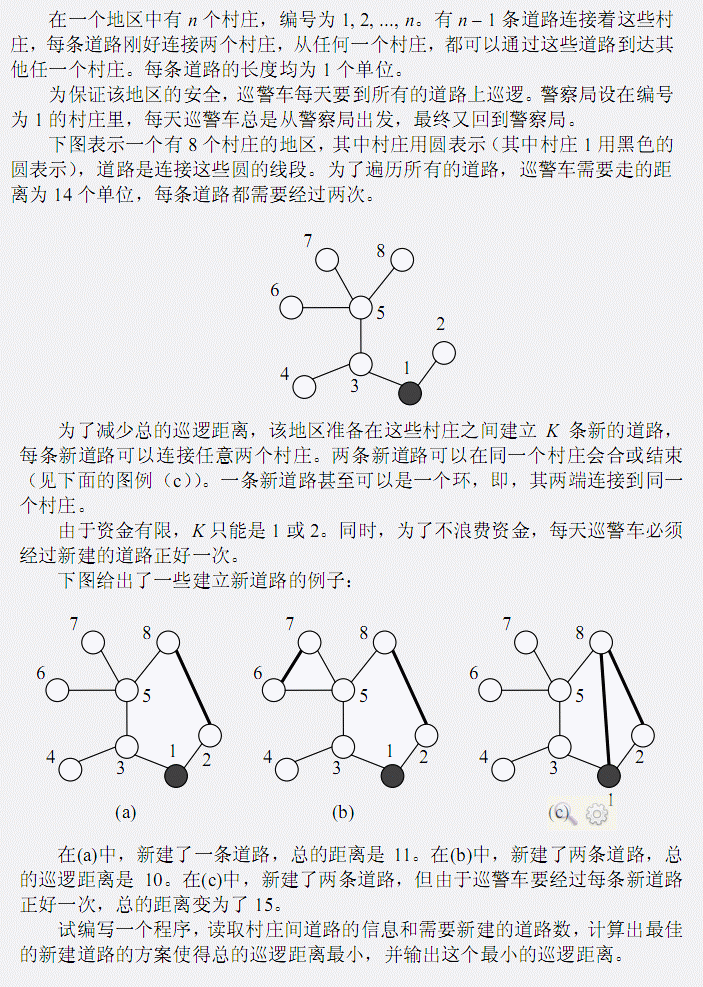
n<=100000
题解:yy一下可以发现,k=1找的是最长链,答案是(n-1)*2+1-长度
k=2的时候,我们把最长链上的边改成-1,然后再跑最长链就行啦。答案是(n-1)*2+2-长度之和。
我一开始yy了很牛逼的树形dp,然后写了半天还是有一个点过不了。。。百度一下题解,真的妙
#include<iostream> #include<cstdio> #define MN 100000 using namespace std; inline int read() { int x = 0 , f = 1; char ch = getchar(); while(ch < '0' || ch > '9'){ if(ch == '-') f = -1; ch = getchar();} while(ch >= '0' && ch <= '9'){x = x * 10 + ch - '0';ch = getchar();} return x * f; } struct edge{int to,next,w;}e[MN*2+5]; int head[MN+5],cnt=0,n; int f[MN+5],w1[MN+5],f1[MN+5],mx[MN+5],mx2[MN+5],ans=0,K,from; void solve(int x,int fa) { int from1=0,from2=0;mx[x]=mx2[x]=f[x]=0; for(int i=head[x];i;i=e[i].next) if(e[i].to!=fa) { solve(e[i].to,x); if(f[e[i].to]+e[i].w>mx[x]) mx2[x]=mx[x],mx[x]=f[e[i].to]+e[i].w,from2=from1,from1=e[i].to; else if(f[e[i].to]+e[i].w>mx2[x]) mx2[x]=f[e[i].to]+e[i].w,from2=e[i].to; } if(mx[x]+mx2[x]>ans) ans=mx[x]+mx2[x],from=x; f[x]=mx[x];mx[x]=from1;mx2[x]=from2; } void relabel(int x) { for(int i=head[x];i;i=e[i].next) if(e[i].to==mx[x]) e[i].w=-1,relabel(e[i].to); } void ins(int f,int t) { e[++cnt]=(edge){t,head[f],1};head[f]=cnt; e[++cnt]=(edge){f,head[t],1};head[t]=cnt; } int main() { n=read();K=read(); for(int i=1;i<n;i++) ins(read(),read()); solve(1,0);if(K==1)return 0*printf("%d",2*n-1-ans); n=n*2-ans;ans=0; for(int i=head[from];i;i=e[i].next) if(e[i].to==mx[from]||e[i].to==mx2[from]) e[i].w=-1,relabel(e[i].to); solve(1,0); printf("%d ",n-ans); return 0; }
3.signaling 信号覆盖

题意:给定平面上n个点,满足没有三个点共线,没有四个点共圆。你现在随意选出三个点,求这三个点的外接圆内包含的点的期望个数。 $nleqslant 1500$
题解:对于每一个三个点包含一个点的情况,我们都能抽象成一个四边形。我们发现凸四边形有两种方法盖住四个点,而凹多边形只有一种方法,所以凸多边形的贡献是2,凹的是1,他们的个数相加是C(n,4),所以我们只要计算凸多边形或者凹多边形的个数就行了。我们枚举凹多边形的凹点,然后按照极角排序,然后枚举一个点,找出最远的点使得他们之间的夹角不超过平角,通过组合算出个数,最后除以总的方案数C(n,3) 。
复杂度$n^{2}logn$
#include<iostream> #include<cstdio> #include<cmath> #include<algorithm> #define MN 1500 #define ll long long using namespace std; inline int read() { int x = 0 , f = 1; char ch = getchar(); while(ch < '0' || ch > '9'){ if(ch == '-') f = -1; ch = getchar();} while(ch >= '0' && ch <= '9'){x = x * 10 + ch - '0';ch = getchar();} return x * f; } struct P { double x,y,alpha; void getAlpha(double xx,double yy){alpha=atan2(x-xx,y-yy);} friend double cross(P a,P b){return a.x*b.y-a.y*b.x;} bool operator == (P b){return x==b.x&&y==b.y;} bool operator < (const P &b) const {return alpha<b.alpha;} P operator - (P b){return (P){x-b.x,y-b.y};} void print() { cout<<x<<" "<<y<<" "<<alpha<<endl; } }p[MN+5],pt[MN+5]; int n,top; double ans=0; ll work(P th) { ll sum=1LL*(n-3)*(n-1)*(n-2)/6;int num=0;top=2; for(int i=1;i<n;i++,--num) { while(cross(p[i]-th,p[top]-th) <= 0) { top=top%(n-1)+1,num++; if(top==i) break; } sum-=1LL*(num)*(num-1)/2; } return sum; } int main() { n=read();if(n==3) return 0*puts("3"); for(int i=1;i<=n;i++) pt[i].x=p[i].x=read(),pt[i].y=p[i].y=read(); for(int i=1;i<=n;i++) { for(int j=1;j<n;j++) { if(pt[i]==p[j]) swap(p[j],p[n]); p[j].getAlpha(pt[i].x,pt[i].y); } sort(p+1,p+n); ans+=work(pt[i]); } double A=1LL*n*(n-1)*(n-2)/6,B=1LL*n*(n-1)*(n-2)*(n-3)/24; printf("%.6lf ",(ans+2*(B-ans))/A+3); return 0; }