1. 问题
给定一定无负值圈的图G,顶点集为V,使用Dijkstra算法求出G中顶点n到顶点m的最短路径,使用Floyd算法求出多源的最短路径,具体的图如下
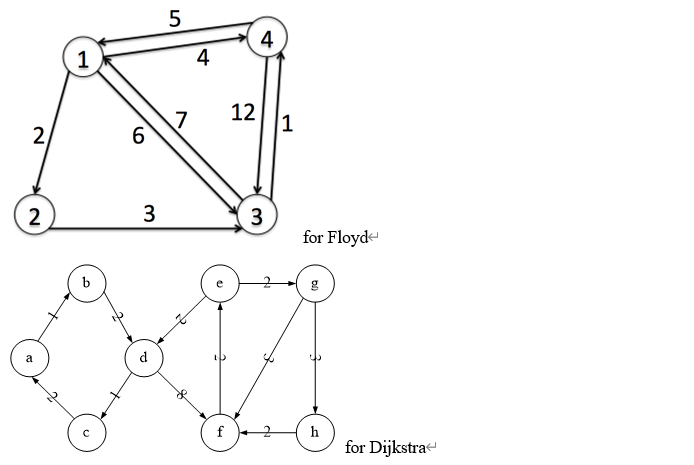
2. 解析
Dijkstra算法是单源的最短路径算法,即给定一个起始点m,求出m到所有其他顶点的最短路径。主要思想是维护一个数组dist与S,S包含了所有已经确定了最短路径的点,对于dist来说|dist| == |V|,对于任意的dist[n],代表了从m为起始点,经过S中的顶点所确定的最短路径。算法的主要流程是:
1.选定dist中未确定的顶点中值最小的顶点i,将i添加进S
2.根据添加的顶点i,来更新dist中的值
3.重复12直到找不到符合条件的顶点
Floyd算法是多源最短路径算法,即可以求出任意的点m属于V,m到所有其他顶点的最短路径。主要思想是来维护两个二维数组D和P,对于D来说,任意的D[m][n],表示了从m点到n点,最多经过一个点的最短距离。对于P来说了,任意的P[m][n],表示了从m点到n点的最短距离所经过的点。对于任意两点m,n来说,都可能存在一个点k,使得D[m][k]+D[k][n]<D[m][n],如果满足上述条件,则对D进行更新,通过对所有存在的点进行一遍遍历,就可以得到任意两点之间的最短路径距离。而在P中存储的就是,这条路径具体的路线。以上图为例,最开始的邻接矩阵如图所示,D中代表了从m到n的距离(不经过任何点),P则代表了最短距离所经过的点。
第一次遍历后,对于第一个点进行检查,判断是否存在m,n,使得使得D[m][1]+D[1][n]<D[m][n],第一次更新后的图如下:

第二次更新后加上了第二个点:
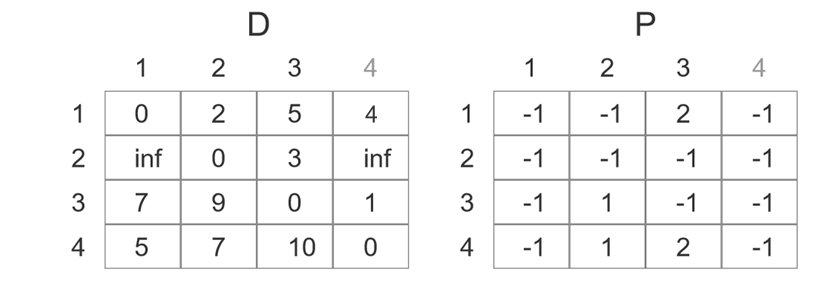
第三次更新后:
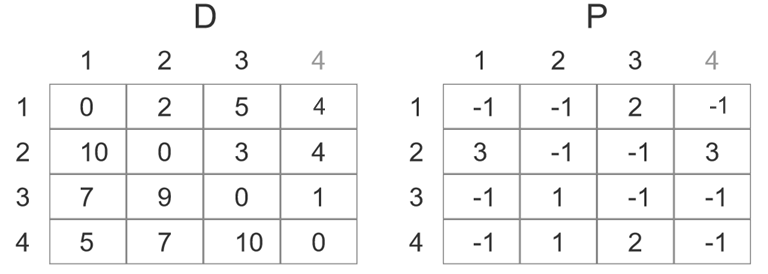
第四次更新后就是所有点之间的最短路径了:
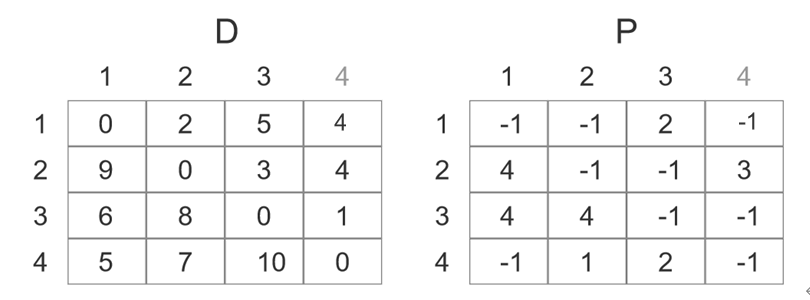
如果要寻找路径,则可以根据P这个矩阵去递归的寻找。
3. 设计
[核心伪代码]
Dijkstra:
While(1){
V = 找到未确定的点中dist最小的点
If(找不到V)
Break
确定V
For(V的所有邻接点V1)
{
If(V1未确定)
Dist[V1] = min(dist[V]+<V,V1> , dist[V1])
}
}
Floyd:
D = G的邻接矩阵
For(k = 1;k <= G.vertex ;k++)
For(i = 1;I <= G.vertex;i++)
For(j = 1;j <= G.vertex;j++)
If(D[i][k]+D[k][j]<D[i][j])
{
D[i][j] = D[i][k]+D[k][j];
P[i][j] = k;
}
4. 分析
Dijkstra算法的时间复杂度,首先对于最外面的while循环,这个循环会执行|V|次,对于循环内部去遍历邻接点的操作,最多会执行|V|次,因此整个算法的时间复杂度是O(|V|2)
Floyd算法的时间复杂度是O(|V|3),因为主要内容就是三个循环,每个循环都进行了|V|次
针对于Dijkstra算法还是比较好理解的,因为只是单源最短路径,只要维护一个数组就可以了,对于其中的贪心算法的思想也可以理解。但是对于Floyd算法其中的动态规划的思想还是没有理解的很透彻。