搬寝室（经典dp）

分析：设 dp[i][j]为在前 j 件物品中选择 i 对物品时最小的疲劳度

          为使疲劳最小，要拿排序后相邻的两数。从小到大依次递推

         （1）当j == 2*i时

    dp[i][j]=dp[i-2][j-1]+(p[i]-p[i-1])*(p[i]-p[i-1])

         （2）当j > 2*i时

       

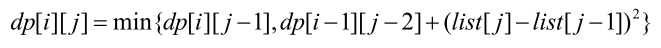
#include <iostream>
#include <stdio.h>
#include <algorithm>

using namespace std;

int list[2001];
int dp[1001][2001];

int main() 
{
    int n,k;
    while(cin >> n >> k)
    {
        for(int i = 1; i <= n; ++i)
            cin >> list[i];
        
        sort(list + 1, list + 1 + n);
        
        for(int i = 0; i <= n; ++i)
            dp[0][i] = 0;
        
        for(int i = 1; i <= k; ++i)
            for(int j = 2 * i; j <= n; ++j)
                if(j == 2 * i)
                    dp[i][j] = dp[i-1][j-2] + (list[j]-list[j-1]) * (list[j]-list[j-1]);
                else
                    dp[i][j] = min(dp[i][j-1], dp[i-1][j-2] + (list[j]-list[j-1]) * (list[j]-list[j-1]));
         
        cout << dp[k][n] << endl;
    }
            
    return 0;
}