The Closest M Points

The Closest M Points

http://acm.hdu.edu.cn/showproblem.php?pid=4347

参考博客：https://blog.csdn.net/acdreamers/article/details/44664645#commentBox

Time Limit: 16000/8000 MS (Java/Others)    Memory Limit: 98304/98304 K (Java/Others)
Total Submission(s): 7461    Accepted Submission(s): 2335

Problem Description

The course of Software Design and Development Practice is objectionable. ZLC is facing a serious problem .There are many points in K-dimensional space .Given a point. ZLC need to find out the closest m points. Euclidean distance is used as the distance metric between two points. The Euclidean distance between points p and q is the length of the line segment connecting them.In Cartesian coordinates, if p = (p₁, p₂,..., p_n) and q = (q₁, q₂,..., q_n) are two points in Euclidean n-space, then the distance from p to q, or from q to p is given by:

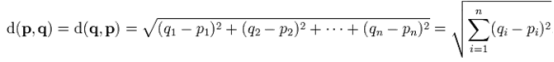
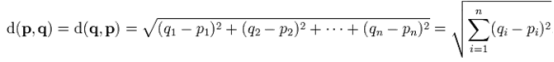
Can you help him solve this problem?

 

Input

In the first line of the text file .there are two non-negative integers n and K. They denote respectively: the number of points, 1 <= n <= 50000, and the number of Dimensions,1 <= K <= 5. In each of the following n lines there is written k integers, representing the coordinates of a point. This followed by a line with one positive integer t, representing the number of queries,1 <= t <=10000.each query contains two lines. The k integers in the first line represent the given point. In the second line, there is one integer m, the number of closest points you should find,1 <= m <=10. The absolute value of all the coordinates will not be more than 10000.
There are multiple test cases. Process to end of file.

 

Output

For each query, output m+1 lines:
The first line saying :”the closest m points are:” where m is the number of the points.
The following m lines representing m points ,in accordance with the order from near to far
It is guaranteed that the answer can only be formed in one ways. The distances from the given point to all the nearest m+1 points are different. That means input like this:
2 2
1 1
3 3
1
2 2
1
will not exist.

 

 

Sample Input

3 2

1 1

1 3

3 4

2

2 3

2

2 3

1

 

Sample Output

the closest 2 points are:

1 3

3 4

the closest 1 points are:

1 3

 

Author

HIT

 

Source

2012 Multi-University Training Contest 5

 

模板题

#include<iostream>
#include<queue>
#include<cstring>
#include<algorithm>
#include<cstdio>
#define N 50005
using namespace std;

int n,m,id;//n是点数,m是维度,id是当前切的维度

struct sair{
    int p[5];
    bool operator<(const sair &b)const{
        return p[id]<b.p[id];
    }
}_data[N],data[N<<3];
int flag[N<<3];

priority_queue<pair<double,sair> >Q;

void build(int l,int r,int rt,int dep){
    if(l>r) return;
    flag[rt]=1;
    flag[rt<<1]=flag[rt<<1|1]=-1;
    id=dep%m;
    int mid=l+r>>1;
    nth_element(_data+l,_data+mid,_data+r+1);
    data[rt]=_data[mid];
  //  if(l==r) return;
    build(l,mid-1,rt<<1,dep+1);
    build(mid+1,r,rt<<1|1,dep+1);
}

void query(sair p,int k,int rt,int dep){
    if(flag[rt]==-1) return;
    pair<double,sair> cur(0,data[rt]);//获得当前节点
    for(int i=0;i<m;i++){//计算当前节点到P点的距离
        cur.first+=(cur.second.p[i]-p.p[i])*(cur.second.p[i]-p.p[i]);
    }
    int idx=dep%m;
    int fg=0;
    int x=rt<<1;
    int y=rt<<1|1;
    if(p.p[idx]>=data[rt].p[idx]) swap(x,y);
    if(~flag[x]) query(p,k,x,dep+1);
    //开始回溯
    if(Q.size()<k){
        Q.push(cur);
        fg=1;
    }
    else{
        if(cur.first<Q.top().first){
            Q.pop();
            Q.push(cur);
        }
        if((p.p[idx]-data[rt].p[idx])*(p.p[idx]-data[rt].p[idx])<Q.top().first){
            fg=1;
        }
    }
    if(~flag[y]&&fg){
        query(p,k,y,dep+1);
    }
}

sair ans[15];

int main(){
    while(~scanf("%d %d",&n,&m)){
        for(int i=1;i<=n;i++){
            for(int j=0;j<m;j++){
                scanf("%d",&_data[i].p[j]);
            }
        }
        build(1,n,1,0);
        int t,k;
        scanf("%d",&t);
        while(t--){
            sair tmp;
            for(int i=0;i<m;i++){
                scanf("%d",&tmp.p[i]);
            }
            scanf("%d",&k);
            while(!Q.empty()){
                Q.pop();
            }
            printf("the closest %d points are:
",k);
            query(tmp,k,1,0);
            for(int i=0;i<k;i++){
                ans[i]=Q.top().second;
                Q.pop();
            }
            for(int i=k-1;i>=0;i--){
                for(int j=0;j<m;j++){
                    if(!j) printf("%d",ans[i].p[j]);
                    else printf(" %d",ans[i].p[j]);
                }
                printf("
");
            }
        }
    }
}