语法分析的作用是处理词法分析得到的记号流建立语法树(又称分析树), 并且建立符号表处理语法错误。
本文约定大写英文字母A、B、C等表示非终结符;小写英文字母a、b、c等表示终结符;小写希腊字母α、β、δ等表示任意记号序列
上下文无关文法
上下文无关文法(Context Free Grammar,CFG)可以表示大多数程序设计语言的语法,又足够简单让我们实现相应的分析器。
文法由四元组定义:
-
非终结符(Nonterminals)集合
-
终结符(Terminals)集合
-
开始符号(Start Symbol)
-
产生式(productions)
所谓产生式是替换规则, 在进行推导时产生式左侧的记号序列可以由右侧记号替换。如产生式E=>E+E中表示表达式可以表示为两个表达式相加。
产生式的推导具有自反性和传递性。若产生式右侧为空串则称为空产生式。
所谓上下文无关文法是指所有产生式左侧仅有一个非终结符, 上下文有关文法中存在形如aAb=>α的产生式。
上下文无关文法允许我们任意情况下将左侧记号替换为右侧序列,让我们更容易构建分析器。BNF(巴克斯-诺尔范式)经常用来表达上下文无关文法。
定义算术表达式中的产生式:
-
E=>(E)
-
E => E+E
-
E => -E
展示一下算术表达式-(a+b)的推导过程:
E => -E => -(E) => -(E+E) => -(E+b) => -(a+b)
或者以分析树的形式表示:

自底向上看分析树我们对原表达式采用了从右到左的分析顺序,这种顺序称为最右推导或正规推导。对应地, 有最左推导的定义。
我们尝试对算术表达式a*b+c按照不同优先级不同推导方式不同分别建立语法树:
-
最左推导乘法优先:
E => E+E => E*E+E => a*E+E => a*b+E => a*b+c -
最左推导加法优先:
E => E*E => E*(E+E) => a*(E+E) => a*(b+E) => a*(b+c) -
最右推导乘法优先:
E => E+E => E*E+E => E*E+c => E*b+C => a*b+c -
最右推导加法优先:
E => E*E => E*(E+E) => E*(E+c) => E*(b+c) => a*(b+c)
可以看出推导的结果仅与文法和句子有关与推导方法无关。自底向上看语法树, 高优先级的生成式会被先处理。
若某一文法对一个句子有多棵分析树则称文法是二义的。避免二义性需要规定产生式的优先级和结合性或者修改文法。
作为表达能力更强的上下文无关文法一定可以表示正规式, 但是正规式不一定可以表示上下文无关文法。
将正规式转换为上下文无关文法的流程如下:
-
构造正规式的NFA;
-
若0为初态,则A0为开始符号;
-
对于move(i,a)=j,引入产生式Ai => aAj;
-
对于move(i,ε)=j,引入产生式 A i=> Aj;
-
若i是终态,则引入产生式Ai => ε。
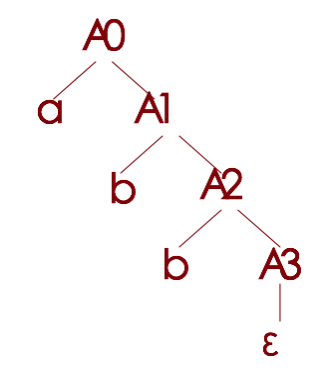
示例, 从正规式r=(a|b)*abb的NFA构造CFG:

A0 => aA0|bA0|aA1
A1 => bA2
A2 => bA3
A3 => ε
自顶向下语法分析
语法分析是对输入序列进行最左推导,尝试建立它的语法树,最终得到一条合法句子或发现错误的过程。
自上而下分析是一个试探回溯的过程, 尝试一切可能建立与输入序列匹配的语法树。
消除左递归
若存在形如A=>Aα|β的生成式时我们称文法存在直接左递归, 直接左递归会使最左推导语法分析陷入死循环中必须加以消除。
若A=>Aα|β中A不是β的前缀(即β不以A开头)则可以将产生式用两个产生式替换:
A => βA'
A' => αA' | ε
这样原来的左递归被替换为右递归, 而右递归不会导致最左推导陷入死循环。
文法E => E+T | T 存在直接左递归, 根据代换规则替换为两个产生式:
E => TE'
E'=> +TE' | ε
用原文法分析a+b: E => E+T => a+T => a+b, 当然我们根据经验避免了左递归。
使用消除左递归后的文法分析a+b: E => TE' => T+TE' => T+T => a+T => a+b
有些文法不含直接左递归,但通过推导可以得到左递归产生式:
- S => Qc | c
- Q => Rb | b
- R => Sa | a
经过推导可以得到左递归产生式: S => Qc => Rbc => Sabc。
消除间接左递归的基本思想是将间接左递归转换为直接左递归, 再将直接左递归转换为右递归。
首先产生式将产生式重新排列为可以迭代的顺序: A[i] => A[i+1]α | β; A[i+1] => A[i+2]α | β; ...。上文中的示例已经满足该条件不必调整。
将3.代入2.中得到4.: Q => (Sa | a)b | b => Sab | ab | b
将4.代入1.中得到5.: S => (Sab | ab | b)c | c => Sabc | abc | bc | c
消除5.中的直接左递归得到6.: S => abcS’| bcS'| cS'; S' => abcS' | ε
从开始符号S出发不会经过QR, 可以将1,2,3, 4删去仅保留5,6作为新文法。
递归下降分析
递归下降分析法是指为记号流中特定非终结符编写一个子程序, 当发现该终结符时即调用该子程序进行分析。
我们规定*优先从左向右处理记号流, 尝试分析1*1+1*1。
自左向右扫描记号流, 发现相应运算符即交由子程序处理。注意因为*优先,则+更靠近分析树根部, 所以应优先调用+的子程序, 其次为*子程序, 最后对的1处理完成后返回。
调用栈即代表语法树:

LL文法分析
LL分析器是一种处理上下文无关文法的自顶向下的语法分析器, 它从左到右处理输入,再对句型执行最左推导出语法树故称为LL分析器。
LL分析器是一种预测分析器, 与普通递归下降分析器不同,预测分析器会向后探查来决定当前语法树结构从而避免回溯。
若一个LL分析器向前探查k个记号(token), 那我们称该分析器为LL(k)分析器, 其中最常用是设计简单且可以处理大多数情况的LL(1)分析器。
给定上下文无关文法:
(1) S => E
(2) S => (S + E)
(3) E => i
试图对((i+i)+i)进行最左推导:
S => (S+E) => ((S+E)+E) => ((E+E)+E) => ((i+E)+E) => ((i+i)+E) => ((i+i)+i)
从状态2(S+E)推导状态3时我们有两个选择S=>(S+E)或者S=>E。在示例中选择任何一种推导都无关紧要, 但在某些情况下做出错误选择后不得不进行回溯。
LL分析法可以通过探查后面的记号来做出决定, 理论上说对任何上下文无关语言总存在k,使得LL(k)无法识别的记号流可以被LL(k+1)识别。
LL分析器依赖分析表来进行决策, 分析表根据后面的记号和当前状态决定下一步状态转移:
| - | + | ( | ) | i |
|---|---|---|---|---|
| S | - | 2 | - | 1 |
| E | - | - | - | 3 |
LL分析器维护一个记号栈, 用于保存待处理的记号. LL分析器首先在栈中压入语法树的根元素, 然后根据记号流中的下一个记号对栈顶元素进行推导, 当栈顶元素无需继续处理时弹出栈顶。当栈为空时语法分析结束。
我们尝试使用LL(1)分析器对(i+i)进行分析:
-
记号栈首先压入语法树的根元素
S, 记号栈为:[S] -
从记号流读入
(,读取栈顶S, 根据分析表应用规则(2)将S改写为(S+E), 记号栈为:[(,S,+,E,)] -
从记号流读入
i, 栈顶(无需推导弹出, 处理新栈顶S: 根据分析表应用规则(1)将S改写为E,记号栈为:
[E,+,E,)] -
处理栈顶
E, 应用规则(3)将记号栈改写为:[i, +, E, ) ] -
根据读入的
i和+依次丢弃栈顶i和+。 -
根据栈顶
E和读入的i, 改写记号栈:[i,)] -
读入
), 弹出栈顶分析完毕。
自底向上语法分析
实际应用中语法分析器更多地从记号流开始建立分析树, 而非从根元素开始建立语法树。加上自底向上分析法更强大, 大多数实用编译器均采用自底向上分析法。
LR分析器是典型的自底向上分析法, 它从左向右处理记号流并尝试进行最右推导。
给定上下文无关文法:
(1) S => E
(2) S => S + E
(3) E => i
LR分析器可以执行几种特定动作:
-
r: reduce应用语法规则化简
-
p: push将下一个记号入栈
-
a: accept分析完成, 记号流被文法接受
-
e: error发现语法错误
若记号流分析完毕没有发现错误,则认为记号流被文法接受。
LR分析器同样需要一个记号栈和一个分析表。分析表根据当前状态和下一个记号决定动作, 为了便于描述, 我们根据记号栈来描述状态:
| - | i | + |
|---|---|---|
| [] | r(3),r(1) | p |
| [ S ] | e | p |
| [S, +] | r(3) | e |
| [S, +, E] | r(2) | e |
尝试对i+i进行LR分析
-
读入
i压栈,依次逆用(3), (1)此时记号栈为:[S] -
读入
+压栈, 此时记号栈为:[S, +] -
读入
i压栈, 逆用(3)此时记号栈为:[S,+, E] -
逆用(2), 此时记号栈为
[S]
至此分析结束, 得到语法树:
S => S + E => S + i => E + i => i + i