数据特征分析-统计分析

一、统计分析

统计分析是对定量数据进行统计描述，常从集中趋势和离中趋势两个方面分析。

集中趋势：指一组数据向某一中心靠拢的倾向，核心在于寻找数据的代表值或中心值-统计平均数（算数平均数和位置平均数）

　　算术平均数：简单算术平均数和权重算术平均数

　　位置平均数：中位数和众数

离中趋势：

　　极差和分位差

　　标准差和方差

二、集中趋势

随机生成整数和总和为1的百分占比

df = pd.DataFrame({'value':np.random.randint(1,100,100),'f':np.random.rand(100)})
df['f'] = df['f']/df['f'].sum()

算术平均数

mean = df['value'].mean()
mean_f = (df['value'] * df['f']).sum()/df['f'].sum()
print('简单算术平均数：%.2f'%mean)
print('权重算术平均数：%2.f'%mean_f)
# 简单算术平均数：48.34
# 权重算术平均数：51

位置平均数

m = df['value'].mode().tolist()   #Seris数据类型可通过tolist()或to_list()转化为列表
med = df['value'].median()
print('众数为：',m)
print('中位数为：',med)
# 众数为： [85]
# 中位数为： 48.0

集中趋势密度图

df['value'].plot(kind = 'kde')

plt.axvline(mean,linestyle='--',color = 'r')
plt.text(mean+5,0.002,'简单算术平均数',color = 'r')

plt.axvline(mean_f,linestyle='--',color = 'y')
plt.text(mean_f+5,0.004,'加权算术平均数',color = 'y')

plt.axvline(med,linestyle='--',color = 'g')
plt.text(med - 30,0.006,'中位数',color = 'g')

三、离中趋势

随机生成DataFrame，表示对应日期的销量

df = pd.DataFrame({'A_sale':np.random.rand(30)*1000,'B_sale':np.random.rand(30)*1000},index = pd.date_range('2019/6/1','2019/6/30'))

极差和分位差

a_jc = df['A_sale'].max() - df['A_sale'].min()
b_jc = df['B_sale'].max() - df['B_sale'].min()
print('产品A销售额极差为%.2f,产品B销售额极差为%.2f'%(a_jc,b_jc))

a_des = df['A_sale'].describe()
b_des = df['B_sale'].describe()
a_iqr = a_des['75%'] - a_des['25%']
b_iqr = b_des['75%'] - b_des['25%']
print('产品A销售额分位差为%.2f,产品B销售额分位差为%.2f'%(a_iqr,b_iqr))
# 产品A销售额极差为968.05,产品B销售额极差为946.94
# 产品A销售额分位差为550.63,产品B销售额分位差为479.76

箱型图展示离散关系

df.boxplot(vert = False)

假设有n个样本，x1、x2...xn，算术平均数为x
方差：( (x1-x)^2 + (x2-x)^2 + ...+ (xn-x)^2 )/n
标准差：方差的平方根

a_std = df['A_sale'].std()
a_var = df['A_sale'].var()
b_std = df['B_sale'].std()
b_var = df['B_sale'].var()
print('产品A销售额标准差为%.2f,方差为%.2f'%(a_std,a_var))
print('产品B销售额标准差为%.2f,方差为%.2f'%(b_std,b_var))
# 产品A销售额标准差为304.25,方差为92565.69
# 产品B销售额标准差为297.36,方差为88424.61

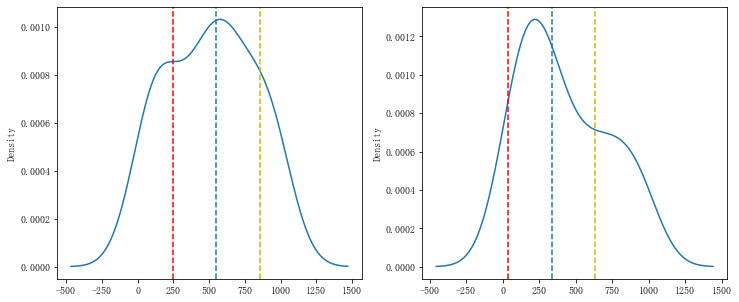
密度图展示中位数、方差

fig = plt.figure(figsize = (12,5))
ax1 = fig.add_subplot(1,2,1)
df['A_sale'].plot(kind = 'kde')
plt.axvline(a_des['50%'] - a_std,linestyle = '--',color = 'r')
plt.axvline(a_des['50%'],linestyle = '--')
plt.axvline(a_des['50%'] + a_std,linestyle = '--',color = 'y')


ax2 = fig.add_subplot(1,2,2)
df['B_sale'].plot(kind = 'kde')
plt.axvline(b_des['50%'] - b_std,linestyle = '--',color = 'r')
plt.axvline(b_des['50%'],linestyle = '--')
plt.axvline(b_des['50%'] + b_std,linestyle = '--',color = 'y')