tarjan+dp——luoguP3687 [ZJOI2017]仙人掌

开篇题外话：没想到tarjan写挂了的我调了一个上午我太蒻了

Problem：luogu  loj

简意：给一张无向图，求有多少种加边方案使得这张图是一个仙人掌（即任意两个环没有共边）

注意：有多组数据

---

Solotion：tarjan（求桥+判断原图）+树形dp

拆环+判断原图：

对于一个仙人掌，我们画图分析可得绝对不能有一条边连接了环两边的端点（下图即为有边连接了环两边的点）

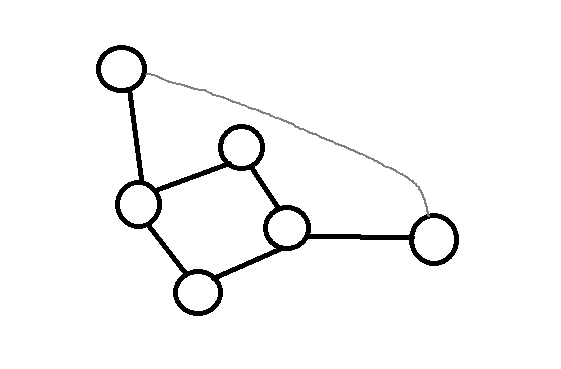
所以这个时候我们可以把环拆掉使得原图变成森林，这个时候我们选择求桥（关于桥（也叫作割边）是什么，点此了解 ）求出桥后我们只走桥就可以走完一颗子树，当然求割点也是一样的，不走连接两个非割点的边即可走完每一棵子树

在求桥的时候可以顺便判断原图是否是仙人掌（方法就是在tarjan的时候如果对于一个根节点u，它的子结点们有多于一个的low[  ]小于dfn[  ]说明一定有两环共边）

code：（fl为bool变量，判断这个图是否是仙人掌，如果不是直接输出0）

inline void tarjan(int u,int fa){
    bool flag=0;
    dfn[u]=low[u]=++dfs_time;
    for(int i=head[u],v;i;i=e[i].nxt){
        v=e[i].to;
        if(vis[i]||vis[e[i].op])    continue;
        vis[i]=1;
        if(!dfn[v]){
            tarjan(v,u);
            low[u]=min(low[u],low[v]);
            if(dfn[u]>low[v]){
                if(flag)    {fl=0;return;}
                flag=1;
            }
            if(dfn[u]<low[v]){
                tag[i]=tag[e[i].op]=1;
            }
        }else{
            low[u]=min(low[u],dfn[v]);
            if(dfn[u]>dfn[v]){
                if(flag)    {fl=0;return;}
                flag=1;
            }
        }
    }
}

预处理：g[ ]

我们用g[i]表示i个数里面两两匹配的方案数，至于为什么要两两匹配，因为如果多个匹配的话所构成的环会有共边（不理解就手画√）

不难得出状态转移方程：

树形dp step：（以下都假设这张图是有方案使得加边后是仙人掌）

我们假设数组 f[u][0]表示以u为根节点的子树内部的连接方案数，f[u][1]表示子树内部往根节点的祖先方向连接的方案数。

（以下左图为f[u][0]，右图f[u][1]）

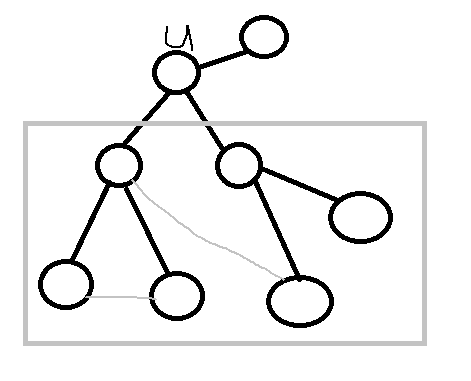
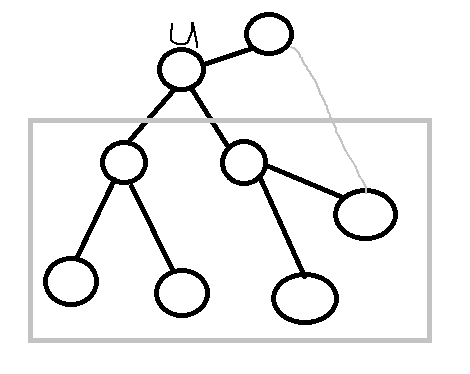
定义　　也就是把u的所有子树的方案数相乘（因为不会互相冲突嘛）对于每个子树把f[u[]0]和f[u][1]相加（因为两者会互相冲突，即如果子树内部连成环之后子树的结点又往外连会造成两环共边）

假设s为以u为根节点的子树个数

 （以u为根节点的子树的内部连接方案数（包括v的子孙节点往外连边）等于v的总方案数乘上u的s个子节点两两连接的方案数（容易知道这不会有两环共边的情况））

 （相当于把一个v单独拿开把它往上连接，剩下的结点内部连接，一共有s个点可以拿开（可能不是很好理解（对 我语文不是很好）多想想实在不行就感性理解吧，也有可能有其他更好理解的方法反正自己理解了就好！））

所以最后答案是f[root][0]（因为root没有祖先结点了）

这个时候我们发现 f[u][0]和f[u][1]其实可以合并成一个f[u]数组（因为对于根节点来说需要的是 f[u][0]和f[u][1]的和，如果无法理解不合并也可以）

所以 　　（根据上述内容我们可以发现更新f[u]的时候不需要加上sum*g[s-1]*s）

code：

void dp(int u){
    vis[u]=1;
    int sum=1,s=0;
    for(int i=head[u],v;i;i=e[i].nxt){
        v=e[i].to;
        if(vis[v]||!tag[i])    continue;
        dp(v);s++;
        sum=(sum*f[v])%mod;
    }
    f[u]=(sum*g[s])%mod;
    if(u!=root)    f[u]=(f[u]+((sum*g[s-1])%mod)*s%mod)%mod;
}

---

Attention：

每一次进行计算的时候，都要mod一遍，因为有可能炸longlong（诚实）

---

完整代码：

#include<iostream>
#include<cstdio>
#include<cstring>
#define int long long
using namespace std;
const int N=5e5+6,M=1e6+6,mod=998244353;
struct node{
    int fro,to,nxt,op;
}e[M<<1];
int T,n,m,cnt,dfn[N],low[N],dfs_time,g[N],f[N],ans=1,head[N],root;
bool vis[M<<1],tag[M<<1],fl=1;
inline void clean(){
    for(int i=1;i<=(m<<1);i++)    tag[i]=vis[i]=0;
    for(int i=1;i<=n;i++)    head[i]=dfn[i]=low[i]=f[i]=0;
    ans=fl=1;cnt=dfs_time=0;
}
inline void add(int x,int y){
    e[++cnt]=(node){x,y,head[x],cnt+1};
    head[x]=cnt;
    e[++cnt]=(node){y,x,head[y],cnt-1};
    head[y]=cnt;
}
inline void tarjan(int u,int fa){
    bool flag=0;
    dfn[u]=low[u]=++dfs_time;
    for(int i=head[u],v;i;i=e[i].nxt){
        v=e[i].to;
        if(vis[i]||vis[e[i].op])    continue;
        vis[i]=1;
        if(!dfn[v]){
            tarjan(v,u);
            low[u]=min(low[u],low[v]);
            if(dfn[u]>low[v]){
                if(flag)    {fl=0;return;}
                flag=1;
            }
            if(dfn[u]<low[v]){
                tag[i]=tag[e[i].op]=1;
            }
        }else{
            low[u]=min(low[u],dfn[v]);
            if(dfn[u]>dfn[v]){
                if(flag)    {fl=0;return;}
                flag=1;
            }
        }
    }
}
void dp(int u){
    vis[u]=1;
    int sum=1,s=0;
    for(int i=head[u],v;i;i=e[i].nxt){
        v=e[i].to;
        if(vis[v]||!tag[i])    continue;
        dp(v);s++;
        sum=(sum*f[v])%mod;
    }
    f[u]=(sum*g[s])%mod;
    if(u!=root)    f[u]=(f[u]+((sum*g[s-1])%mod)*s%mod)%mod;
}
signed main(){
    scanf("%lld",&T);
    g[1]=g[0]=1;
    for(int i=2;i<=N-5;i++)
        g[i]=(g[i-1]+(g[i-2]*(i-1))%mod)%mod;
    while(T--){
        scanf("%lld%lld",&n,&m);
        clean();
        for(int i=1,u,v;i<=m;i++){
            scanf("%lld%lld",&u,&v);
            add(u,v);
        }
        tarjan(1,0);
        if(!fl){
            printf("0\n");
            continue;
        }
        for(int i=1;i<=n;i++)    vis[i]=0;
        for(int i=1;i<=n;i++)
            if(!vis[i]){
                root=i;
                dp(i);
                ans=(ans*f[i])%mod;
            }
        printf("%lld\n",ans);
    }
    return 0;
}