Window Pains
| Time Limit: 1000MS | Memory Limit: 65536K | |
| Total Submissions: 2524 | Accepted: 1284 |
Description
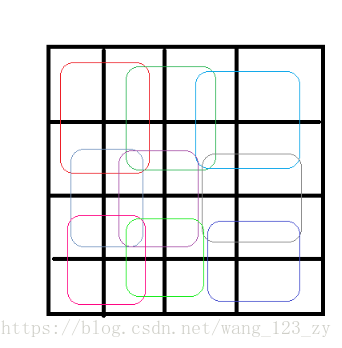
Boudreaux likes to multitask, especially when it comes to using his computer. Never satisfied with just running one application at a time, he usually runs nine applications, each in its own window. Due to limited screen real estate, he overlaps these windows and brings whatever window he currently needs to work with to the foreground. If his screen were a 4 x 4 grid of squares, each of Boudreaux's windows would be represented by the following 2 x 2 windows:
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
When Boudreaux brings a window to the foreground, all of its squares come to the top, overlapping any squares it shares with other windows. For example, if window 1and then window 2 were brought to the foreground, the resulting representation would be:
|
If window 4 were then brought to the foreground: |
|
. . . and so on . . .
Unfortunately, Boudreaux's computer is very unreliable and crashes often. He could easily tell if a crash occurred by looking at the windows and seeing a graphical representation that should not occur if windows were being brought to the foreground correctly. And this is where you come in . . .
Input
Input to this problem will consist of a (non-empty) series of up to 100 data sets. Each data set will be formatted according to the following description, and there will be no blank lines separating data sets.
A single data set has 3 components:
- Start line - A single line:
START
- Screen Shot - Four lines that represent the current graphical representation of the windows on Boudreaux's screen. Each position in this 4 x 4 matrix will represent the current piece of window showing in each square. To make input easier, the list of numbers on each line will be delimited by a single space.
- End line - A single line:
END
After the last data set, there will be a single line:
ENDOFINPUT
Note that each piece of visible window will appear only in screen areas where the window could appear when brought to the front. For instance, a 1 can only appear in the top left quadrant.
Output
For each data set, there will be exactly one line of output. If there exists a sequence of bringing windows to the foreground that would result in the graphical representation of the windows on Boudreaux's screen, the output will be a single line with the statement:
THESE WINDOWS ARE CLEAN
Otherwise, the output will be a single line with the statement:
THESE WINDOWS ARE BROKEN
Sample Input
START
1 2 3 3
4 5 6 6
7 8 9 9
7 8 9 9
END
START
1 1 3 3
4 1 3 3
7 7 9 9
7 7 9 9
END
ENDOFINPUT
Sample Output
THESE WINDOWS ARE CLEAN
THESE WINDOWS ARE BROKEN题意
有9个程序窗口在4*4的矩阵中,每个程序窗口占用2*2矩阵的空间,编号为1~9。如下图(画的有点乱,应该能看懂)
在这些程序窗口中存在相互覆盖的关系,给出9*9的数字矩阵,每个数字表示程序窗口。问这样的相互覆盖关系是否合理
思路
拓扑排序模板题。但是建图太难了T_T,建好图进行拓扑排序,判断排序之后还有没有相连的边就行了
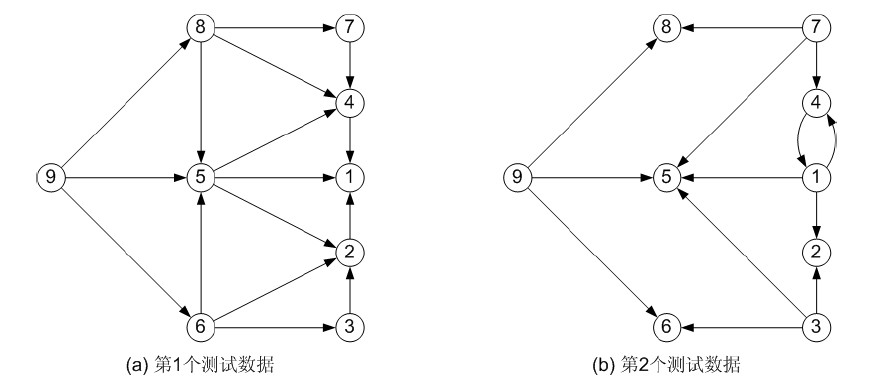
样例中的建好的图如下图(图片来自http://www.cnblogs.com/pony1993/archive/2012/08/16/2641904.html)
AC代码
#include <stdio.h>
#include <string.h>
#include <iostream>
#include <algorithm>
#include <math.h>
#include <limits.h>
#include <map>
#include <stack>
#include <queue>
#include <vector>
#include <set>
#include <string>
#define ll long long
#define ms(a) memset(a,0,sizeof(a))
#define pi acos(-1.0)
#define INF 0x3f3f3f3f
const double E=exp(1);
const int maxn=1e3+10;
using namespace std;
int a[maxn][maxn];
int vis[maxn];
int b[maxn][maxn];
void toposort()
{
for(int i=1;i<=9;i++)
{
for(int j=1;j<=9;j++)
{
if(vis[j]==0)
{
vis[j]--;
for(int k=1;k<=9;k++)
{
if(b[j][k])
{
b[j][k]--;
vis[k]--;
}
}
break;
}
}
}
}
int main(int argc, char const *argv[])
{
ios::sync_with_stdio(false);
string str;
string st;
while(cin>>str)
{
ms(vis);
ms(a);
ms(b);
if(str=="ENDOFINPUT")
break;
for(int i=1;i<=4;i++)
for(int j=1;j<=4;j++)
cin>>a[i][j];
cin>>st;
for(int i=1;i<=3;i++)
{
for(int j=1;j<=3;j++)
{
for(int ii=0;ii<2;ii++)
{
for(int jj=0;jj<2;jj++)
{
if(a[i+ii][j+jj]==j+(i-1)*3)
continue;
else if(b[a[i+ii][j+jj]][j+(i-1)*3]==0)
{
b[a[i+ii][j+jj]][j+(i-1)*3]=1;
vis[j+(i-1)*3]++;
}
}
}
}
}
toposort();
int flag=0;
for(int i=1;i<=9;i++)
{
for(int j=1;j<=9;j++)
{
flag+=b[i][j];
}
}
if(flag)
cout<<"THESE WINDOWS ARE BROKEN"<<endl;
else
cout<<"THESE WINDOWS ARE CLEAN"<<endl;
}
return 0;
}