code1796 社交网络

输入描述 Input Description

输入文件中第一行有两个整数，n 和 m，表示社交网络中结点和无向边的数 目。在无向图中，我们将所有结点从 1 到 n 进行编号。 接下来 m 行，每行用三个整数 a, b, c 描述一条连接结点 a 和 b，权值为 c 的 无向边。注意任意两个结点之间最多有一条无向边相连，无向图中也不会出现自 环（即不存在一条无向边的两个端点是相同的结点）。

输出描述 Output Description

输出文件包括 n 行，每行一个实数，精确到小数点后 3 位。第 i 行的实数表 示结点 i 在社交网络中的重要程度

样例输入 Sample Input

4 4

1 2 1

2 3 1

3 4 1

4 1 1

样例输出 Sample Output

1.000

1.000

1.000

1.000

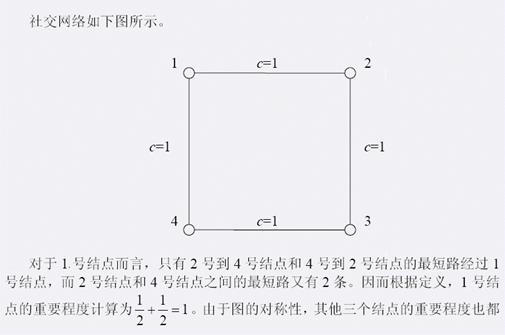为1

Folyd算法，在求最短路的同时处理c数组，然后再计算I数组。具体见代码。

代码：

#include<iostream>
#include<cstring>
#include<cstdio>
#define Size 105
using namespace std;

int n,m;
double g[Size][Size];
double c[Size][Size];
double I[Size];

int main(){
    cin>>n>>m;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
            g[i][j]=1e15,c[i][j]=0;
    int a,b; double w;
    for(int i=1;i<=m;i++){
        cin>>a>>b>>w;
        g[a][b]=g[b][a]=w;
        c[a][b]=c[b][a]=1;
    }
    
    for(int k=1;k<=n;k++){
        for(int i=1;i<=n;i++){
            for(int j=1;j<=n;j++){
                if(k==i||k==j||i==j)continue;
                if(g[i][k]+g[k][j]<g[i][j]){
                    g[i][j]=g[i][k]+g[k][j];
                    c[i][j]=0;
                }
                if(g[i][k]+g[k][j]==g[i][j]){
                    c[i][j]+=c[i][k]*c[k][j];
                }
            }
        }
    }
    /*
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++){
            cout<<c[i][j]<<' ';
        }
        cout<<endl;
    }
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++){
            cout<<g[i][j]<<' ';
        }
        cout<<endl;
    }
    */
    for(int k=1;k<=n;k++){
        for(int i=1;i<=n;i++){
            for(int j=1;j<=n;j++){
                if(k==i||k==j||i==j)continue;
                if(g[i][k]+g[k][j]==g[i][j]&&c[i][j]>0){
                    I[k]+=c[i][k]*c[k][j]/c[i][j];
                }
            }
        }
    }
    for(int i=1;i<=n;i++)printf("%.3lf
",I[i]);
    return 0;
}