题
OvO <- http://acm.hdu.edu.cn/showproblem.php?pid=6086
( 2017 Multi-University Training Contest - Team 5 - 1002 )
解
首先,如果没要求左右对称的话
对所有给定串,建一个AC自动机,
开一个dp数组,dp[i][j][k]代表长度为i的时候,状态在AC自动机上第j个节点,匹配到的串的状态为k(将匹配到哪些给定串的状态压缩),所得到的串的数量
然后遍历长度i=(0~m-1),对于每个i遍历AC自动机上的节点j=(0~ac.T-1),对于每个j用k遍历ac自动机的字符集(‘0’和‘1’)
nxt=next[j][k],表示节点j对于字符k的转移后的节点,flag为节点j所能取到的状态(对其fail数组递归)
然后对于dp[i][j][k]向后转移。
那么状态转移为 dp[i+1][nxt][k|flag]=dp[i+1][nxt][k|flag]+dp[i][j][k]。
那么加左右对称的条件的话,我们对于每个给定串,对于每个字符前的空位,判断是否根据这个空位翻转,
具体翻转:
以11001为例,下文'|'表示对称轴的位置
1. 首先是对于第一个空,也就是第一个1前面的空(|11001),可以对其整体作翻转,
11001翻转后变为10011,然后取反,也就是01100,也就是说,在长度为1~L的串中匹配到了01100的话,那后半部分必然有一个11001,
所以可以把01100插入到AC自动机里。
2. 对于第二个空,(1|1001),
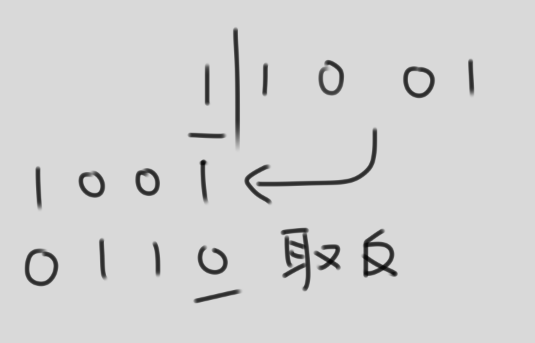
很明显有下划线的1和0匹配不上,所以舍弃这次翻转。
3. 对于第三个空位(11|001)

这是合法的,结果串为011,可见如果在计算长度为L的串的dp值时候,如果匹配到了011串,那么整个2L串中是有11001这个串的,
那么就可以把这个串插入AC自动机中,另外做一个标记,表示这个匹配只在计算长度为L的串时才有效。
4. 对于剩下几个空位的翻转与上面类似
这样dp数组就需要开得很大,所以把dp[i][j][k]的第1维改成滚动数组。计算dp数组的时候只要计算长度为L的串的数量即可。
(赛时少写了一个与操作和一个等于号,卡了2小时,淦 O∧O)
#include <stdio.h>
#include <string.h>
#include <iostream>
#include <algorithm>
#include <queue>
using namespace std;
struct Trie
{
static const int MAX_SIZE=500044;
static const int CHRSET_SIZE=54;
static const int HASH_SIZE=144441;
int chrset_size;
int hash[HASH_SIZE];
int next[MAX_SIZE][CHRSET_SIZE],fail[MAX_SIZE],end[MAX_SIZE],end2[MAX_SIZE];
int root,L;
int gethash(char key[])
{
int len = strlen(key);
for(int i=0;i<len;i++)
hash[key[i]]=i;
}
int newnode()
{
for(int i = 0;i < chrset_size;i++)
next[L][i] = -1;
end2[L] = 0;
end[L++] = 0;
return L-1;
}
void init(char key[])
{
chrset_size=strlen(key);
gethash(key);
L = 0;
root = newnode();
}
void insert(char s[],int num,int flag)
{
int len = strlen(s);
int now = root;
for(int i = 0;i < len;i++)
{
if(next[now][hash[s[i]]] == -1)
next[now][hash[s[i]]] = newnode();
now=next[now][hash[s[i]]];
}
if(flag==1)
end[now]|=(1<<num);
else
end2[now]|=(1<<num);
}
void build()
{
queue<int>Q;
fail[root] = root;
for(int i = 0;i < chrset_size;i++)
if(next[root][i] == -1)
next[root][i] = root;
else
{
fail[next[root][i]] = root;
Q.push(next[root][i]);
}
while(!Q.empty())
{
int now = Q.front();
Q.pop();
for(int i = 0;i < chrset_size;i++)
if(next[now][i] == -1)
next[now][i] = next[fail[now]][i];
else
{
fail[next[now][i]] = next[fail[now]][i];
Q.push(next[now][i]);
}
}
}
int query(char buf[])
{
int len = strlen(buf);
int now = root;
int ret = 0;
for(int i = 0;i < len;i++)
{
now = next[now][hash[buf[i]]];
int temp = now;
while(temp != root)
{
ret += end[temp];
end[temp] = 0;
temp = fail[temp];
}
}
return ret;
}
} ac;
const int mod=998244353;
int n;
char key[44];
char str[144];
char str2[144];
int dp[2][8044][70];
int ans;
void solve(int m)
{
int i,j,t,nxt,tmp,flag,wh,k;
memset(dp,0,sizeof(dp));
dp[0][0][0]=1;
t=m;
for(t=0;t<m;t++)
{
wh=t&1;
memset(dp[1-wh],0,sizeof(dp[1-wh]));
for(i=0;i<ac.L;i++)
for(j=0;j<ac.chrset_size;j++)
{
tmp=nxt=ac.next[i][j];
flag=0;
flag|=ac.end[nxt];
if(t+1==m)
flag|=ac.end2[nxt];
while(ac.fail[tmp]!=0)
{
tmp=ac.fail[tmp];
flag|=ac.end[tmp];
if(t+1==m)
flag|=ac.end2[tmp];
}
// cout<<t<<' '<<i<<' '<<j<<' '<<nxt<<' '<<flag<<' '<<1-wh<<' '<<n<<endl;
for(k=0;k<=(1<<n)-1;k++)
dp[1-wh][nxt][k|flag]=(0ll+dp[1-wh][nxt][k|flag]+dp[wh][i][k])%mod;
}
// printf("
");
// for(i=0;i<ac.L;i++)
// {
// for(k=0;k<=(1<<n)-1;k++)
// printf("%d",dp[wh][i][k]);
// printf(" ");
// }
// printf("
");
// for(i=0;i<ac.L;i++)
// {
// for(k=0;k<=(1<<n)-1;k++)
// printf("%d",dp[1-wh][i][k]);
// printf(" ");
// }
// printf("
");
}
ans=0;
for(i=0;i<ac.L;i++)
ans=(0ll+ans+dp[m&1][i][(1<<n)-1])%mod;
printf("%d
",ans);
}
int main()
{
bool flagstr;
int cas,i,j,t;
int L,len,len2;
scanf("%d",&cas);
while(cas--)
{
scanf("%d%d",&n,&L);
for(i=0;i<2;i++)
key[i]='0'+i;
key[2]='�';
ac.init(key);
for(i = 0;i < n;i++)
{
scanf("%s",str);
ac.insert(str,i,1);
len=strlen(str);
for(j=0;j<len;j++)
{
flagstr=true;
if(j>len-j)
{
for(t=0;t<j;t++)
str2[t]=str[t];
str2[j]='�';
for(t=0;t<len-j;t++)
if(str[j+t]==str2[j-(t+1)])
{
flagstr=false;
break;
}
}
else
{
for(t=len-1;t>=j;t--)
str2[len-(t+1)]='0'+1-(str[t]-'0');
str2[len-j]='�';
for(t=0;t<j;t++)
if(str[t]==str[j+(j-t)-1])
{
flagstr=false;
break;
}
}
// cout<<j<<' '<<str2<<' '<<flagstr<<endl;
if(j==0)
{
ac.insert(str2,i,1);
continue;
}
if(flagstr)
ac.insert(str2,i,2);
}
}
ac.build();
solve(L);
}
return 0;
}
/*
10
2 2
0
1
2 2
011
001
2 3
011
001
*/