牛客网暑期ACM多校训练营（第一场）A Monotonic Matrix(数学公式+思维)

题目链接： https://www.nowcoder.com/acm/contest/139/A 

先备知识

LGV 算法 (Lindström–Gessel–Viennot lemma)

wiki链接：https://en.wikipedia.org/wiki/Lindstr%C3%B6m%E2%80%93Gessel%E2%80%93Viennot_lemma


求以上矩阵的行列式，其中 e(a,b) 是从a到b的方法数，带入求行列式即可得到(a1,a2,...an) 到 (b1,b2,...bn) 的所有不相交路径的种数

思路

考虑01和12的分界线
是(n, 0)到(0，m)的两条不相交（可重合）路径
分界线以及分界线以上的点是一种，分界线下是一种
平移其中一条变成(n-1, -1)到(-1，m-1);
变成

然后进行预处理打表前2*n的阶乘和阶乘逆元就行了

 

 

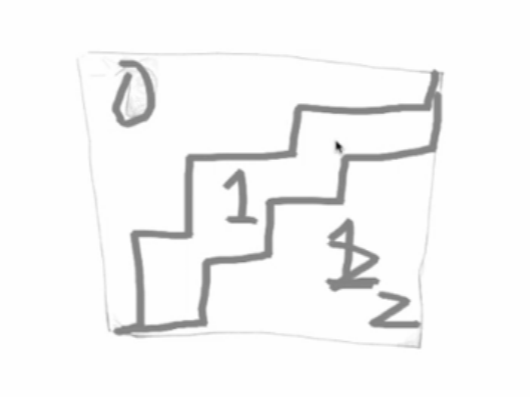
大致图形：

#include<bits/stdc++.h>
using namespace std;
 
const int N=2005,mo=1e9+7;
 
int C[N][N];
 
int main(){
    C[0][0]=1;
    for (int i=1;i<N;i++){
        C[i][0]=1;
        for (int j=1;j<=i;j++) C[i][j]=(C[i-1][j-1]+C[i-1][j])%mo;
    }
    int n,m;
    while(~scanf("%d%d",&n,&m)){
        printf("%lld
",(1ll*C[n+m][n]*C[n+m][n]%mo-1ll*C[n+m][n+1]*C[n+m][n-1]%mo+mo)%mo);
    }
}