HDU 4366 Successor

题意：给你一棵树，求树中某节点子树中能力值大于它且忠诚度最高的那个。

在第一次看到这个问题是，我有一个疑问：

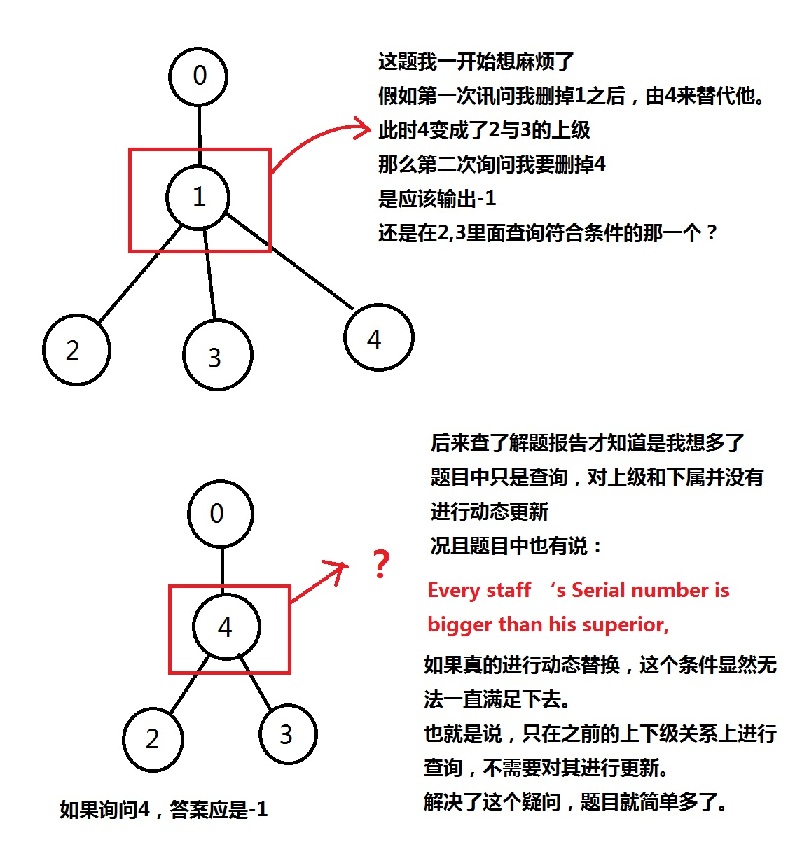
解决这个问题有两个关键点：

1.树形结构到线性结构的转换

原因：员工关系整棵树是一棵结构不确定的树，员工编号不一定连续，对于查询其符合条件的下属有很大困难（只能暴力）。而编号之后可以将子树映射到编号连续的一段区间，这时就可以用线段树快速查询最值。
做法：用邻接表保存树，从根开始DFS，记录每棵子树的起始端点和终止端点。

2.对能力值从大到小进行排序，按能力值从大到小的顺序加入线段树，能力值相同时，编号小的在前面。

原因：因为每次要查找能力值大于该人且忠诚度最高的那个下属，所以当该点插入线段树时，线段树中已有的节点全部是能力值高于他的人，所以只需要在这群人中，属于其下属的子树区间内查询一下忠诚度的最值即可。
做法：线段树节点用于保存最高忠诚度。细节见代码。

#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <algorithm>

#define lson l, m, rt << 1
#define rson m + 1, r, rt << 1 | 1

using namespace std;

const int MAXN = 50002;

struct staff      //员工节点
{
    int superior;
    int ability;
    int loyalty;
};

struct node       //邻接表保存树
{
    int v;
    int next;
};

struct subTree    //存储子树的起始编号和终止编号
{
    int st;
    int ed;
};

int N, Q;
int EdgeN, dfs_clock;
//邻接表保存树
node D[MAXN];
int head[MAXN];

int ans[MAXN];     //存储答案

staff F[MAXN];
subTree sub[MAXN];   //存储编号为i的员工，其下属的起始编号和终止编号

int maxi[ MAXN << 2 ];   //线段树，存储忠诚度的最大值

int vis[ 1000010 ];      //忠诚度→编号映射

bool cmp( staff a, staff b )
{
    return a.ability > b.ability;
}

void AddEdge( int u, int v )    //头插法加点
{
    D[EdgeN].v = v;
    D[EdgeN].next = head[u];
    head[u] = EdgeN++;
    return;
}

void DFS( int cur )             //DFS遍历，记录其子树的起始编号和终止编号
{
    sub[cur].st = dfs_clock++;
    for ( int i = head[cur]; i != -1; i = D[i].next )
        DFS( D[i].v );
    sub[cur].ed = dfs_clock;
}

void init()                     //初始化
{
    EdgeN = 1;
    memset( head, -1, sizeof(head) );
    memset( maxi, -1, sizeof(maxi) );
    dfs_clock = 1;
    return;
}

int query( int L, int R, int l, int r, int rt )   //区间查最值
{
    if ( L <= l && r <= R ) return maxi[rt];

    int m = ( l + r ) >> 1;

    int ret = -1;
    if ( L <= m ) ret = max( ret, query( L, R, lson ) );
    if ( R > m )  ret = max( ret, query( L, R, rson ) );

    return ret;
}

void PushUp( int rt )
{
    maxi[rt] = max( maxi[ rt << 1 ], maxi[ rt << 1 | 1 ] );
    return;
}

void update( int id, int val, int l, int r, int rt )   //节点加入线段树
{
    if ( l == id && r == id )
    {
        maxi[rt] = val;
        return;
    }

    int m = ( l + r ) >> 1;
    if ( id <= m ) update( id, val, lson );
    else update( id, val, rson );

    PushUp( rt );
    return;
}

int main()
{
    int T;
    scanf( "%d", &T );
    while ( T-- )
    {
        init();

        scanf( "%d%d", &N, &Q );
        for ( int i = 1; i < N; ++i )
        {
            int a, aby, loy;
            scanf( "%d%d%d", &a, &loy, &aby );
            AddEdge( a, i );
            F[i].ability = aby;
            F[i].loyalty = loy;
            F[i].superior = a;
            vis[loy] = i;
        }

        DFS( 0 );  //根节点编号为0

        sort( F + 1, F + N, cmp );  //按能力值从大到小排序

        int j;
        for ( int i = 1; i < N; i = j )
        {
            j = i;
            while ( j < N && F[i].ability == F[j].ability )
            {
                int id = vis[ F[j].loyalty ];
                int tp = -1;
                if ( sub[id].st + 1 <= sub[id].ed - 1 )
                    tp = query( sub[id].st + 1, sub[id].ed - 1, 1, dfs_clock - 1, 1 );
                if ( tp == -1 ) ans[id] = -1;
                else ans[id] = vis[tp];
                ++j;
            }

            j = i;
            while ( j < N && F[i].ability == F[j].ability )
            {
                int id = vis[ F[j].loyalty ];
                update( sub[id].st, F[j].loyalty, 1, dfs_clock - 1, 1 );
                ++j;
            }
        }

        while ( Q-- )
        {
            int a;
            scanf( "%d", &a );
            printf( "%d\n", ans[a] );
        }
    }
    return 0;
}