需求:
有时候当移动速度很慢,GPS定位的轨迹点就非常的多,这时候为了缩减数据量,需要将不突出的点去掉。
思路:
(1) 在曲线首尾两点间虚连一条直线,求出其余各点到该直线的距离。
(2)选其最大者与阈值相比较,若大于阈值,则离该直线距离最大的点保留,否则将直线两端点间各点全部舍去。
(3)依据所保留的点,将已知曲线分成两部分处理,重复第1、2步操作,迭代操作,即仍选距离最大者与阈值比较,依次取舍,直到无点可舍去,最后得到满足给定精度限差的曲线点坐标
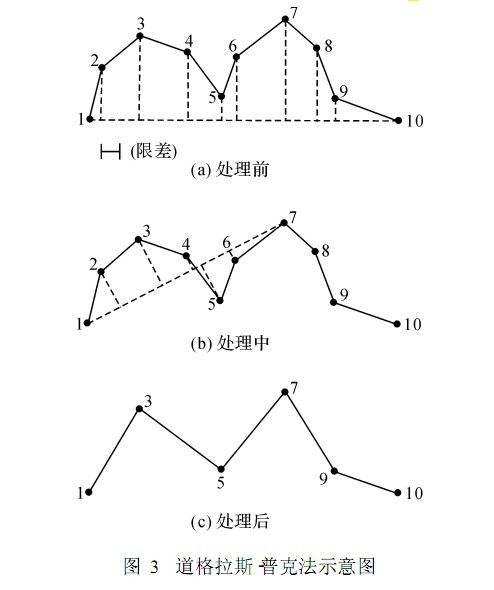
这里使用道格拉斯-普克算法实现,易于理解。效果对比图如下:

源代码:
<!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http://www.w3.org/TR/xhtml1/DTD/xhtml1-transitional.dtd"> <html xmlns="http://www.w3.org/1999/xhtml"> <head> <meta http-equiv="Content-Type" content="text/html; charset=utf-8"/> <title>DouglasPeucker</title> </head> <body> <canvas id="drawing" style="height:300px;100%"></canvas> <canvas id="drawing2" style="height:300px;100%"></canvas> </body> <script type="text/javascript" > var points1=[]; var pointsshao=[]; var pts=[]; var hval=30;//阈值 //随机生成1000个点 for(var i=0;i<1000;i++){ var oldx=i*10,oldy=Math.random()*150; points1.push([oldx,oldy,i]); } //求斜率 function xielv(pt1,pt2) { var k,b; var canshu={}; canshu.k=(pt1[1]-pt2[1])/(pt1[0]-pt2[0]); canshu.b=pt1[1]-canshu.k*pt1[0]; return canshu; } //求点到直线的距离 function distanceToline(pt,cs){ return (Math.abs(cs.k*pt[0]-pt[1]+cs.b))/Math.sqrt(cs.k*cs.k+1); } //开始计算(道格拉斯普克算法) pts.push(points1[0]); countPoint(points1); pts.push(points1[points1.length-1]); //排序 function sort(pts){ for(var i=0;i<pts.length-1;i++) { var a=pts[i]; var b=pts[i+1]; if(b[2]>a[2]){ pts[i]=b; pts[i+1]=a; for(var j=i;j>0;j--) { var c=pts[j-1]; if(b[2]>c[2]){ pts[j-1]=b; pts[j]=c; } } } } } //对坐标点进行取舍 function countPoint(points){ var maxD=0; var maxPoint=null; var maxindex=0; //大于2个点才开始计算 if(points.length>2){ var pt1=points[0]; var pt2=points[points.length-1]; var cs=xielv(pt1,pt2); for(var i=0;i<points.length;i++){ var pt=points[i]; var dis=distanceToline(pt,cs); //判断该线段中是否有点到由该线段端点组成的直线的距离大于限值 if(dis>maxD) { maxD=dis; maxPoint=pt; maxindex=i; } } if(maxD>hval) //如果最大值就从该点位置将线段进行切分 { var pts1=points.slice(maxindex);//中分末尾数组 var pts2=points.slice(0,maxindex+1);//中分前面数组 if(pts1.length>2 && pts2.length>2) { if(!countPoint(pts1) && !countPoint(pts2)){ //如果两个线段都没有超过限制就结束计算 pts.push(maxPoint); } }else if(pts1.length>2 && pts2.length<=2){ //计算pts1 if(!countPoint(pts1))pts.push(maxPoint); }else if(pts1.length<=2 && pts2.length>2){ //计算pts2 if(! countPoint(pts2))pts.push(maxPoint); } } return false; } } //由大到小 sort(pts); drawWay("drawing2",pts); drawWay("drawing",points1)
//绘制曲线 function drawWay(name,points){ var drawing=document.getElementById(name); if(drawing.getContext){ var context=drawing.getContext("2d"); context.beginPath(); var oldx=points[0][0]; var oldy=points[0][1]; for(var i=0;i<points.length;i++){ var p=points[i]; context.moveTo(oldx,oldy); oldx=p[0]; oldy=p[1]; context.lineTo(oldx,oldy); } context.closePath(); context.stroke(); } } </script>