前言:
这篇题解真的写了很久,改了又改才成为这样的,我不会写题解但我正在努力去学,求通过,求赞。。。
题目:
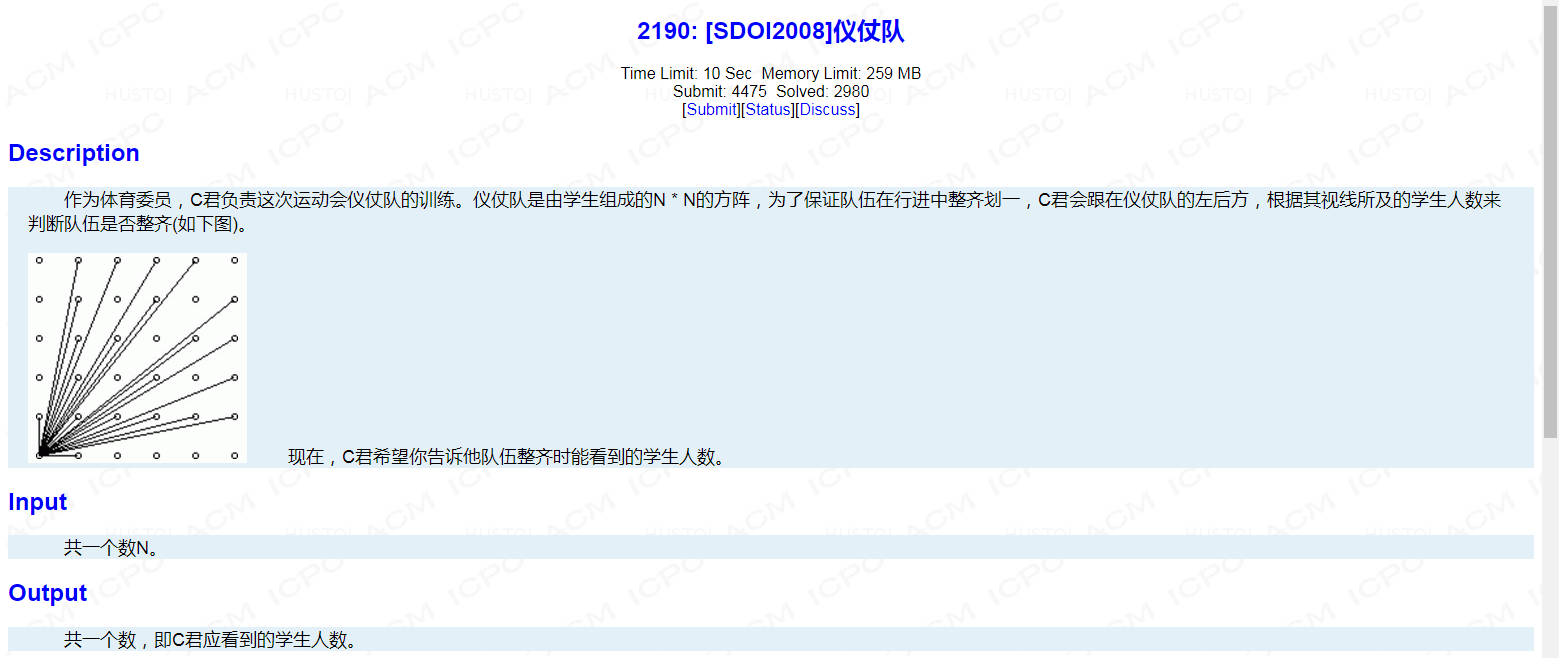
思路:
像我这样的数论菜鸡就不能一秒切这题,怎么办呢?
拿个栗子手玩一下:
假设(n=6),我们看看主人公可以看到的人的位置和他自己的位置有什么关系
随便选几个点,((1,4),(2,6),(4,4)),主人公在((6,1))
经过大于几分钟的时间,我发现了一个性质
这样我们就可以枚举(x-x')的值和(y-y')的值了, 但是时间爆炸:

怎么办呢?
(1 leq N leq 40000)这里的话我们原来的(O(n^2))是肯定过不了的,有没有比较快的做法???
废话肯定有啊不然这题出出来了
对噢,我们可以用欧拉函数来做呀!
下面有一篇写得比较好的洛谷日报链接,请先阅读完本篇题解,感兴趣的再点
再给你们看一个东西:

它逆时针旋转45°后左右对称了!
也就是说它拥有对称性。
先放着不管(那你为什么现在放粗来呀)
上面说了,如果要看得到那么要满足(gcd(|~x-x'~|~,~|~y-y'~|) =1)。
我们假设(|~x-x'~|~<~|~y-y'~|)。
如果我们固定了(|~y-y'~|)要找满足条件的(|~x-x'~|)。那么这样一来答案不就是(3+2*sum_{i=2}^{n-1}varphi (i))了?(这里乘(2)是因为我们只做了当(|~x-x'~|~<~|~y-y'~|)的部分,又因上文写道这满足对称性所以我们可以乘(2)。加(3)是因为我们特判了((0,1),(1, 0),(1,1))这(3)点。)
对于(varphi)函数,(varphi (i))表示小于i,且和i互质的数的个数,好了,你看完这句你就可以点开上面那条链接了。
我们可以用一个(O(n~log~n))的埃氏筛去预处理(varphi)函数(见代码部分),或者使用一个(O(n))的来预处理(请自行翻阅资料)。
代码:
关于埃氏筛(varphi)函数:
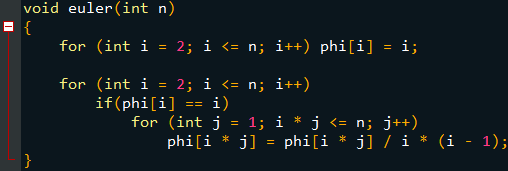
主程序(哎呀,( exttt{int main()})没截到QAQ):
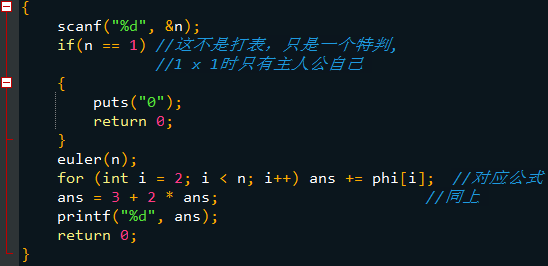
❤感谢收看❤