【2021夏纪中游记】2021.7.17模拟赛

2021.7.17模拟赛

比赛概括：

(mathrm{sum}=0+0+0+0)

唉。

T1 [JOI 2021 Final]有趣的家庭菜园 4：

题目大意：

思路：

(mathcal{O}(n)) 求出需要浇水的前缀和和后缀和，枚举峰值，取最小的最大值即可。

代码：

const int N = 2e5 + 10;

inline ll Read()
{
	ll x = 0, f = 1;
	char c = getchar();
	while (c != '-' && (c < '0' || c > '9')) c = getchar();
	if (c == '-') f = -f, c = getchar();
	while (c >= '0' && c <= '9') x = (x << 3) + (x << 1) + c - '0', c = getchar();
	return x * f;
}

int n;
int a[N], b[N];
ll sum1[N], sum2[N], ans = 1e18;

int main()
{
	n = Read();
	for (int i = 1; i <= n; i++) a[i] = Read();
	for (int i = 2; i <= n; i++) b[i] = a[i] - a[i - 1];
	for (int i = 2; i <= n; i++)
	{if(b[i] <= 0) sum1[i] = -b[i] + 1; sum1[i] += sum1[i-1];}
	for (int i = n; i >= 2; i--)
	{if(b[i] >= 0) sum2[i] = b[i] + 1; sum2[i] += sum2[i+1];}
	for (int k = 1; k <= n; k++)
		ans = min(ans, max(sum1[k], sum2[k + 1]));
	printf ("%lld
", ans);
	return 0;
}

T2 [NOI2018]屠龙勇士：

题目大意：

思路：

stoorz 爷精准押题。

这题可以一眼看出是 ex-CRT：

[left{egin{matrix} b_ix_i &equiv &a_ipmod{p_i} \ &vdots end{matrix} ight.]

那么接下来题目有两个难点：

1. 如何求出每条龙对应哪把剑。
2. (p_i) 不是质数，所以 (b_i) 不能求逆元，该如何处理。

第一点，可以通过平衡树、权值线段树等维护。这里也可以偷懒用 multiset。

第二点要剖析 ex-CRT 的本质。详见 emptyset 的博客。

代码：

const int N = 1e5 + 10;

inline ll Read()
{
	ll x = 0, f = 1;
	char c = getchar();
	while (c != '-' && (c < '0' || c > '9')) c = getchar();
	if (c == '-') f = -f, c = getchar();
	while (c >= '0' && c <= '9') x = (x << 3) + (x << 1) + c - '0', c = getchar();
	return x * f;
}

int t, n, m;
ll a[N], p[N];
int b[N], val[N];

ll exgcd(ll a, ll b, ll &x, ll &y)
{
	if (!b)
	{
		x = 1, y = 0;
		return a;
	}
	ll gcd = exgcd(b, a % b, y, x);
	y -= a / b * x;
	return gcd;
}

ll qpow(ll a, ll b, ll mod)
{
	ll ans = 1;
	for (; b; b >>= 1, a = a * a % mod)
		if (b & 1) ans = ans * a % mod;
	return ans;
}

ll mul(ll a, ll b, ll mod)
{
	ll ans = 0;
	for (; b; b >>= 1, a = (a + a) % mod)
		if (b & 1) ans = (ans + a) % mod;
	return ans;
}

ll mx;
multiset <ll> s;

int main()
{
	for (int t = Read(); t--; )
	{
		s.clear();
		n = Read(), m = Read(); mx = 0;
		for (int i = 1; i <= n; i++) a[i] = Read();
		for (int i = 1; i <= n; i++) p[i] = Read();
		for (int i = 1; i <= n; i++) val[i] = Read();
		for (int i = 1; i <= m; i++) s.insert(Read());
		
		for (int i = 1; i <= n; i++)
		{
			multiset<ll>::iterator u = s.upper_bound(a[i]);
			if (u != s.begin()) u--;
			b[i] = *u;
			s.erase(u);
			s.insert(val[i]); // b[i]x > a[i]
			mx = max(mx, (ll)ceil((double)a[i] / b[i]));
		}
		bool HasSolution = 1;
		
		ll lcm = 1, ans = 0;
		for (int i = 1; i <= n; i++)
		{
			ll x, y, gcd = exgcd(lcm * b[i] % p[i], p[i], x, y), A = ((a[i] - b[i] * ans % p[i]) % p[i] + p[i]) % p[i];
			x = (x % p[i] + p[i]) % p[i];
			if (A % gcd) {puts("-1"); HasSolution = 0; break;}
			ans = (ans + mul(A / gcd, x, p[i] / gcd) * lcm % (lcm *= p[i] / gcd)) % lcm;
		}
		if(!HasSolution) continue;
		if (mx > ans) ans = ans + (ll)ceil((double)(mx - ans) / lcm) * lcm;
		printf ("%lld
", ans);
		
	}
	return 0;
}

T3 周长：

题目大意：

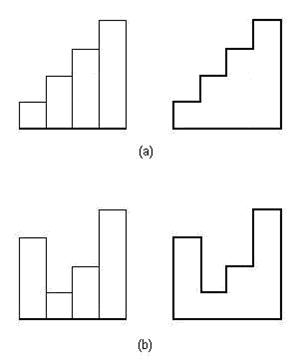
小PP喝饮料中了大奖，奖励n块宽度为1的农田，每一块都有自己的长度，小PP可以自己去选择这N块农田的位置，要按如图的方式拼接在一起。每块农田互不相同（即使长度一样也不同）那么显然有n！种放置方法。不同的方法可以使整个大农田的周长不同，如图(a)周长为16,而图(b)的周长为20.可证明没有比20 更大的周长存在。小PP喜欢绕着农田跑步，他希望最终这个大农田的周长最大。

正文：

考虑状压 DP。设 (f_{i,j},g_{i,j}) 分别表示状态 (i) 当前第 (j) 个块的最大周长及其方案数。转移显然。

代码：

const int N = 20, M = 4e4 + 10;

inline ll Read()
{
	ll x = 0, f = 1;
	char c = getchar();
	while (c != '-' && (c < '0' || c > '9')) c = getchar();
	if (c == '-') f = -f, c = getchar();
	while (c >= '0' && c <= '9') x = (x << 3) + (x << 1) + c - '0', c = getchar();
	return x * f;
}

int n, a[N]; 
ll f[M][N], g[M][N], ans, cnt;

int main()
{
	n = Read();
	for (int i = 1; i <= n; i++) a[i] = Read();
	for (int i = 1; i <= n; i++) f[1 << i-1][i] = 2 * a[i], g[1 << i-1][i] = 1;
	for (int k = 0; k < (1 << n); k++)
		for (int i = 1; i <= n; i++)
			if ((k >> i-1) & 1)
				for (int j = 1; j <= n; j++)
					if(!((k >> j-1) & 1))
					{
						if (f[k | (1 << j-1)][j] < f[k][i] + (a[j] - min(a[i], a[j])) * 2)
							f[k | (1 << j-1)][j] = f[k][i] + (a[j] - min(a[i], a[j])) * 2, 
							g[k | (1 << j-1)][j] = g[k][i];
						else if (f[k | (1 << j-1)][j] == f[k][i] + (a[j] - min(a[i], a[j])) * 2)
							g[k | (1 << j-1)][j] += g[k][i];
					}
	
	for (int i = 1; i <= n; i++)
		if (ans < f[(1 << n) - 1][i] + n * 2) ans = f[(1 << n) - 1][i] + n * 2, cnt = g[(1 << n) - 1][i];
		else if (ans == f[(1 << n) - 1][i] + n * 2) cnt += g[(1 << n) - 1][i];
	
	printf ("%lld %lld
", ans, cnt);
	return 0;
}

T4 [ROIR 2018 Day1]管道监控：

题目大意：

正文：

恶心。

线性规划问题。可以先用 trie 树求解出所有路经的最小花费。考虑建边：

• 源点向根节点连流量 (+infty)、费用 (0) 的边。
• 叶子节点向汇点连流量 (1)、费用 (0) 的边。
• 节点 (i) 向父亲连一条流量叶子数减一、费用 (0) 的边；父亲再连向 (i) 流量为 (+infty) 费用 (0) 的边。
• 如果当前点是某单词的结尾，向开头连流量 (1)、费用 (w) 的边。

由于这个图已经不是 DAG，求增广路时就可以用双端队列。

代码：

const int N = 510, M = 1e6 + 10;
const ll inf = 1e18;

inline ll Read()
{
	ll x = 0, f = 1;
	char c = getchar();
	while (c != '-' && (c < '0' || c > '9')) c = getchar();
	if (c == '-') f = -f, c = getchar();
	while (c >= '0' && c <= '9') x = (x << 3) + (x << 1) + c - '0', c = getchar();
	return x * f;
}

int n, m, t;
int fa[N], siz[N];
char c[N], s[M];

int S, T;
struct edge
{
	ll to, w, val, nxt, id;
}e[M << 1];
int head[N], tot = 1;

void add(int u, int v, ll w, ll val, int id = 0)
{
	e[++tot] = (edge) {v, w, val, head[u], id}, head[u] = tot;
	e[++tot] = (edge) {u, 0, -val, head[v], id}, head[v] = tot;
}

struct Trie
{
	ll tot, t[M][30], val[M], id[M];
	Trie() { memset (val, 0x3f3f3f3f, sizeof val), tot = 1;}
	
	void Insert(char *s, ll cst, ll k)
	{
		ll p = 1, len = strlen (s + 1);
		for (int i = len; i; i--)
		{
			if (!t[p][s[i] - 'a']) t[p][s[i] - 'a'] = ++tot;
			p = t[p][s[i] - 'a'];
		}
		if (val[p] > cst) val[p] = cst, id[p] = k;
	}
	
	void Add(int x)
	{
		ll p = 1;
		for (ll u = x; fa[u]; u = fa[u])
		{
			if (!t[p][c[u] - 'a']) break;
			p = t[p][c[u] - 'a'];
			if (val[p] < inf) add(fa[u], x, 1, val[p], id[p]);
		}
	}
}tr;

int pre[N];
bool vis[N];
ll dis[N], incf;
deque <int> q;
bool SPFA()
{
	memset (dis, 0x3f3f3f3f, sizeof dis);
	while (!q.empty()) q.pop_front();
	q.push_back(S);
	vis[S] = 1; dis[S] = 0;
	while (!q.empty())
	{
		int u = q.front(); q.pop_front();
		vis[u] = 0;
		for (int i = head[u]; ~i; i = e[i].nxt)
		{
			int v = e[i].to;
			if (dis[v] > dis[u] + e[i].val && e[i].w)
			{
				dis[v] = dis[u] + e[i].val;
				pre[v] = i;
				if (!vis[v]) 
				{
					vis[v] = 1;
					if (q.size() && dis[v] <= dis[q.front()]) q.push_front(v);
					else q.push_back(v);
				}
			} 
		}
	}
	return dis[T] < inf;
}


ll cost, maxFlow;
void MCMF()
{
	cost = 0;
	while (SPFA())
	{
		int u = T; incf = inf;
		for (; u != S; u = e[pre[u] ^ 1].to)
			incf = min(incf, e[pre[u]].w);
			
		cost += dis[T] * incf, maxFlow -= incf;
		for (u = T; u != S; u = e[pre[u] ^ 1].to)
			e[pre[u]].w -= incf,
			e[pre[u] ^ 1].w += incf;
	}
	return ;
}


int main()
{
	memset (head, -1, sizeof head);
	n = Read(), m = Read(), t = Read() ^ 1;
	S = N - 1, T = N - 2;
	for (int i = 2; i <= n; i++)
	{
		fa[i] = Read();
		for(c[i] = getchar(); !('a' <= c[i] && c[i] <= 'z'); c[i] = getchar()); 
		siz[i] = 1, siz[fa[i]] = 0;
	}
	add(S, 1, inf, 0);
	for (int i = 1; i <= n; i++)
	{
		if (!siz[i]) continue;
		add(i, T, 1, 0); maxFlow++;
	}
	for (int i = n; i; i--)
	{
		add(fa[i], i, siz[i] - 1, 0);
		add(i, fa[i], inf, 0);
		siz[fa[i]] += siz[i];
	}
	for (int i = 1; i <= m; i++)
	{
		ll val = Read();
		scanf ("%s", s + 1);
		tr.Insert(s, val, i);
	}
	for (int i = 1; i <= n; i++) tr.Add(i);
	
		
	MCMF();
	
	if (maxFlow) {puts("-1"); return 0;}
	
	printf ("%lld
", cost);
	
	if (t) return 0;
	
	cost = 0;
	for (int i = 2; i <= tot; i += 2)
		if (!e[i].w && e[i].id) cost ++;
	printf ("%lld
", cost);
	
	for (int i = 2; i <= tot; i += 2)
		if (!e[i].w && e[i].id) 
			printf ("%d %d %d
", e[i ^ 1].to, e[i].to, e[i].id);
	return 0;
}