【题目描述】
波罗的海上有两个小岛:Bornholm和Gotland。在每个小岛上都有一些神奇的远程通信端口,每个通信端口可以运行在两种模式下——发送模式和接收模式。Bornholm和Gotland分别有n和m个这样的端口,每个端口都连接着另一个小岛某个端口,称为“目标端口”。
请设置这n+m个端口的模式,使得所有端口都处于工作状态,即:
l 对于处于接收模式的端口A,另一个小岛上至少有一个以A为目标端口的端口被设置成发送模式。
l 对于处于发送模式的端口B,它的目标端口必须处于接收状态。
其中1≤n , m≤50000。
如下图(每个点指向的点表示它的目标端口):
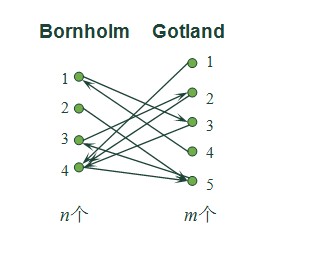
那么它的一种设置方案为:
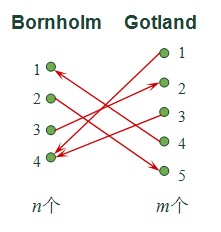
即Bornholm岛上1号、4号端口与Gotland岛上2号、5号端口被设置为接收状态,其他端口被设置为发送状态。
【题目解析】
首先假设B岛的所有端口都设置为发送状态,将G岛的所有端口都设置为接受状态。这样的话,对于所有入度为0的G岛是无用状态,将G岛的这些端口的状态改为发送状态,然后将其对应的B岛的目标端口设置为接受状态,然后更新B岛所连接的G岛目标端口的入度,将新产生的入度为0的G岛的端口作为下一个用于更新的点。
【代码如下】
1 #include <iostream> 2 #include <cstdio> 3 #include <queue> 4 5 using namespace std; 6 7 const int Maxn = 100001; 8 9 struct edge 10 { 11 int v; 12 edge* next; 13 edge(int _v ,edge* _next) : v(_v), next(_next) {} 14 }* E[Maxn]; 15 16 bool Sta[Maxn]; 17 int N, M, Deg[Maxn]; 18 queue <int> Q; 19 20 void Print() 21 { 22 for (int i = 1; i <= N + M; ++i) 23 if (Sta[i]) cout << i << " OUT" << endl; 24 else cout << i << " IN" << endl; 25 } 26 27 void Solve() 28 { 29 for (int i = N + 1; i <= N + M; ++i) 30 if (!Deg[i]) Q.push(i); 31 while (Q.size()) 32 { 33 int i = Q.front(); Q.pop(); 34 Sta[i] = true; 35 for (edge* j = E[i]; j; j = j -> next) 36 { 37 int v = j -> v; 38 if (!Sta[v]) continue; 39 Sta[v] = false; 40 for (edge* k = E[v]; k; k = k -> next) 41 { 42 Deg[k -> v]--; 43 if (!Deg[k -> v]) Q.push(k -> v); 44 } 45 } 46 } 47 } 48 49 inline void edgeAdd(int x, int y) 50 { 51 E[x] = new edge(y, E[x]); 52 } 53 54 void Init() 55 { 56 cin >> N >> M; 57 for (int i = 1; i <= N; ++i) Sta[i] = true; 58 int x, y; 59 while (cin >> x >> y) edgeAdd(x, y), Deg[y]++; 60 } 61 62 int main() 63 { 64 freopen("test.in", "r", stdin); 65 Init(); 66 Solve(); 67 Print(); 68 return 0; 69 }