题目描述
Y901高速公路是一条重要的交通纽带,政府部门建设初期的投入以及使用期间的养护费用都不低,因此政府在这条高速公路上设立了许多收费站。
Y901高速公路是一条由N-1段路以及N个收费站组成的东西向的链,我们按照由西向东的顺序将收费站依次编号为1~N,从收费站i行驶到i+1(或从i+1行驶到i)需要收取Vi的费用。高速路刚建成时所有的路段都是免费的。
政府部门根据实际情况,会不定期地对连续路段的收费标准进行调整,根据政策涨价或降价。
无聊的小A同学总喜欢研究一些稀奇古怪的问题,他开车在这条高速路上行驶时想到了这样一个问题:对于给定的l,r(l<r),在第l个到第r个收费站里等概率随机取出两个不同的收费站a和b,那么从a行驶到b将期望花费多少费用呢?
输入
第一行2个正整数N,M,表示有N个收费站,M次调整或询问
接下来M行,每行将出现以下两种形式中的一种
C l r v 表示将第l个收费站到第r个收费站之间的所有道路的通行费全部增加v
Q l r 表示对于给定的l,r,要求回答小A的问题
所有C与Q操作中保证1<=l<r<=N
输出
对于每次询问操作回答一行,输出一个既约分数
若答案为整数a,输出a/1
样例输入
4 5
C 1 4 2
C 1 2 -1
Q 1 2
Q 2 4
Q 1 4
样例输出
1/1
8/3
17/6
题解
线段树
首先将每次修改和询问的r减1,把线段权值转化为点权值。
然后使用总和/总次数的方式计算期望。
考虑第$i$个点$(lle ile r)$,它被选中的次数为$(i-l+1)*(r-i+1)$,所以所求即为
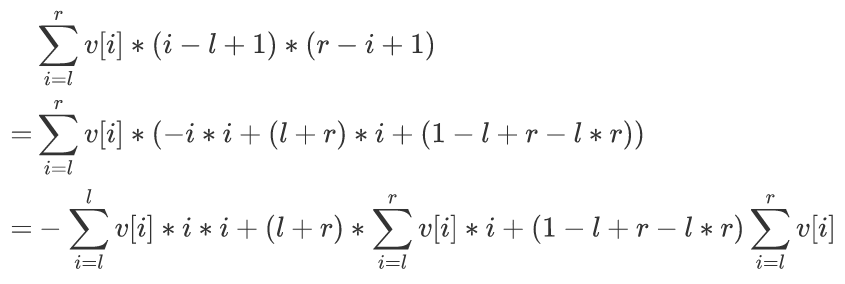
于是直接开3棵线段树维护$v[i]*i*i$、$v[i]*i$、$v[i]$的区间和即可。
注意要开long long。
#include <cstdio>
#include <cstring>
#include <algorithm>
#define N 100010
#define lson l , mid , x << 1
#define rson mid + 1 , r , x << 1 | 1
using namespace std;
typedef long long ll;
struct data
{
ll sum[N << 2] , si[N << 2] , add[N << 2];
void pushdown(int x)
{
if(add[x])
{
sum[x << 1] += add[x] * si[x << 1] , add[x << 1] += add[x];
sum[x << 1 | 1] += add[x] * si[x << 1 | 1] , add[x << 1 | 1] += add[x];
add[x] = 0;
}
}
void build(int flag , int l , int r , int x)
{
if(l == r)
{
if(flag == 0) si[x] = 1;
else if(flag == 1) si[x] = l;
else si[x] = (ll)l * l;
return;
}
int mid = (l + r) >> 1;
build(flag , lson) , build(flag , rson);
si[x] = si[x << 1] + si[x << 1 | 1];
}
void update(int b , int e , ll a , int l , int r , int x)
{
if(b <= l && r <= e)
{
sum[x] += a * si[x] , add[x] += a;
return;
}
pushdown(x);
int mid = (l + r) >> 1;
if(b <= mid) update(b , e , a , lson);
if(e > mid) update(b , e , a , rson);
sum[x] = sum[x << 1] + sum[x << 1 | 1];
}
ll query(int b , int e , int l , int r , int x)
{
if(b <= l && r <= e) return sum[x];
pushdown(x);
int mid = (l + r) >> 1;
ll ans = 0;
if(b <= mid) ans += query(b , e , lson);
if(e > mid) ans += query(b , e , rson);
return ans;
}
}A , B , C;
char str[5];
ll gcd(ll a , ll b)
{
return b ? gcd(b , a % b) : a;
}
int main()
{
int n , m , x , y;
ll z , t , d;
scanf("%d%d" , &n , &m) , n -- ;
A.build(0 , 1 , n , 1) , B.build(1 , 1 , n , 1) , C.build(2 , 1 , n , 1);
while(m -- )
{
scanf("%s%d%d" , str , &x , &y) , y -- ;
if(str[0] == 'C')
scanf("%lld" , &z) , A.update(x , y , z , 1 , n , 1) , B.update(x , y , z , 1 , n , 1) , C.update(x , y , z , 1 , n , 1);
else
{
t = (y - x + 1 - (ll)y * x) * A.query(x , y , 1 , n , 1) + (y + x) * B.query(x , y , 1 , n , 1) - C.query(x , y , 1 , n , 1);
d = gcd(t , (ll)(y - x + 1) * (y - x + 2) / 2);
printf("%lld/%lld
" , t / d , (ll)(y - x + 1) * (y - x + 2) / 2 / d);
}
}
return 0;
}