AcWing 飞行员兄弟

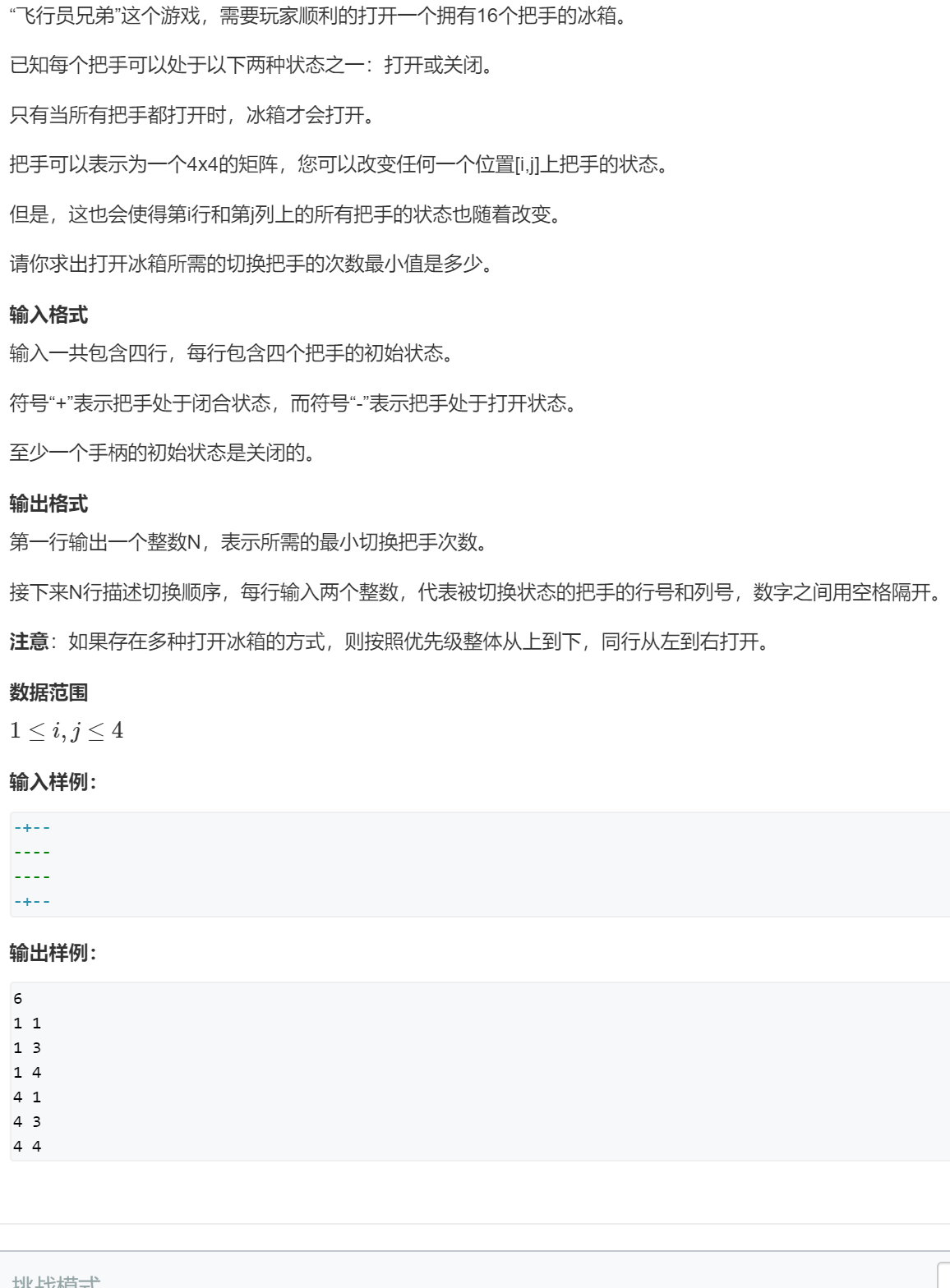
 数据范围非常 小,可以枚举出所有的操作寻找最优解.

如何枚举所有的操作?首先看出来这个问题有这样的性质:

①如果改变了一个把手的状态,那么就没有必要再次改变它.

②改变多个把手状态的顺序对结果没有影响.

所以,所有的操作即为最终对于每把手进行状态切换或者不进行状态切换,也就是选或者不选的问题.

共有16个把手,所以共有2¹⁶种操作方法.现在需要枚举这些操作方法.

在此之前先来看看怎么表示所有把手的状态.

首先把所有把手放到一行来观察,如本题样例变为:

-+-----------+--

用0表示闭合,1表示打开,则可以将这个初始状态表示为:

0100 0000 0000 0100

这可以看作一个用二进制表示的数字,且这个数字是该二进制表示方法唯一表示的,他们是一一映射关系.

那么就可以用二进制下的:

0000 0000 0000 0000 到 1111 1111 1111 1111

来表示所有可能的状态.在十进制下这个区间等价为0 ~ 65535,这个区间里的每一个数都代表了一个状态.

现在就知道表示这些状态的方法了.

现在要根据这些状态进行操作,为了体现把手原本的坐标有如下实现:

// 这里的t即为存储状态的数字
    for(int i = 1; i <= 4; i++)
        for(int j = 1; j <= 4; j++){
            if(t & 1) operations();    // 读取到位置(i, j)上的把手状态为"真"
            t >>= 1;                   // 转移到下一个位置
        } 

到此,就可以将某个状态压缩为一个数字并对其进行读取和需要的处理.

但实际上这题更方便的做法是用数组存储把手状态,而对把手的操作压缩一下.

现在需要枚举所有的操作,根据上文提到的,如果用0表示不改变其状态,用1表示改变其状态,同样可以用二进制下的:

0000 0000 0000 0000 到 1111 1111 1111 1111

来表示.并且有类似地方法来读取每一个坐标上的操作.

有如下实现:

// x 即为存储16个把手操作方法的数字
// tmp 对应输入的原始把手状态,这里用bool数组表示更方便
for(int i = 1; i <= 4 && x; i++)
        for(int j = 1; j <= 4 && x; j++){
            if(x & 1){    // 如果改变了坐标(i,j)的把手的状态,则需要对该行和该列所有把手都切换状态
                for(int k = 1; k <= 4; k++) tmp[k][j] = !tmp[k][j];
                for(int k = 1; k <= 4; k++) tmp[i][k] = !tmp[i][k];
                tmp[i][j] = !tmp[i][j];    // 注意行列交叉点被操作了两次,要再调整一下
            }
            x >>= 1;
        }

最后,题目要求输出进行操作的点的坐标,运用位操作+枚举坐标也可以轻松做到.

AC Code:

#include <algorithm>
#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;

bool s[5][5], tmp[5][5];
int ans = (1 << 16) - 1, ct;

bool check(int x){　　　　// 检查操作 x 能否使所有把手打开
    for(int i = 1; i <= 4 && x; i++)
        for(int j = 1; j <= 4 && x; j++){
            if(x & 1){
                for(int k = 1; k <= 4; k++) tmp[k][j] = !tmp[k][j];
                for(int k = 1; k <= 4; k++) tmp[i][k] = !tmp[i][k];
                tmp[i][j] = !tmp[i][j];
            }
            x >>= 1;
        }
    for(int i = 1; i <= 4; i++)
        for(int j = 1; j <= 4; j++)
            if(!tmp[i][j]) return false;
    return true;
}

void cmp(int x){　　　　// 统计操作 x 进行了多少次操作,即其二进制表示方法有多少个1
    int ct1, ct2, t1 = ans, t2 = x;
    while(t1){
        if(t1 & 1) ct1++;
        t1 >>= 1;
    }
    while(t2){
        if(t2 & 1) ct2++;
        t2 >>= 1;
    }
    if(ct1 > ct2) ans = x;
}

int main(){
    char ch;
    for(int i = 1; i <= 4; i++, getchar())
        for(int j = 1; j <= 4; j++){
            scanf("%c", &ch);
            if(ch == '-') s[i][j] = true;
        }

    for(int i = 0; i <= (1 << 16) - 1; i++){
        memcpy(tmp, s, sizeof(s));
        if(check(i)) cmp(i);
    }

    int t = ans;
    while(t){
        if(t & 1) ct++;
        t >>= 1;
    }
    printf("%d
", ct);
    for(int i = 1; i <= 4; i++)
        for(int j = 1; j <= 4; j++){
            if(ans & 1) printf("%d %d
", i, j);
            ans >>= 1;
        }

    return 0;
}