普及图论三题 P1807 P1113 P 4017

1.最大食物链计数

对于每组数据中的A和B,建立有向边A→B,那么最终构造出一个有向无环图.现在要求出从任意一个入度为0(即不捕食任何生物)的点可达到的出度为0(即不被任何生物捕食)的点的个数之和.

对于任一起点,需要找到其能到达满足条件的终点的路径数,这种问题在数据很小的情况下我成功用搜索求解过,这题的数据应该记忆化,这是计数DP.

设想有这样一个点1,总共有若干条路径可以直接到达它:

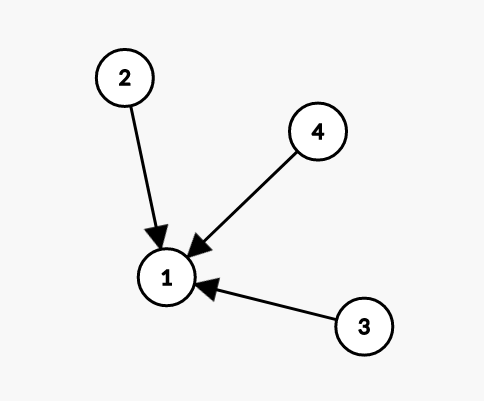
 那么到达点1的路径数就是到达点2,3,4各自的路径数之和.

因此按照某种方式从起点遍历到终点,最终就可以得出到达任一终点的路径数.而这某种方式,你觉得是不是和拓扑排序有关?按照拓扑序遍历,可以使得类似于上图中2,3,4的点总是在1之前遍历,初始状态,起点到达自己的路径数当然是1.

使用队列进行处理,将入度为0的点放到队列中进行初始化,处理过程中发现是终点(即出度为0)则累加到答案中.

#include <algorithm>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
const int MOD = 80112002;

vector<int> s[5010];
queue<int> q;
int n, m, ru[5010], chu[5010], ct[5010];
int ans;

int main() {
    scanf("%d%d", &n, &m);
    while (m--) {
        int x, y;
        scanf("%d%d", &x, &y);
        s[x].push_back(y);
        ru[y]++, chu[x]++;
    }

    for(int i = 1; i <= n; i++)
        if(!ru[i]) q.push(i), ct[i] = 1;

    while(!q.empty()){
        int cur = q.front();
        q.pop();
        if(!chu[cur]){
            ans = (ans + ct[cur]) % MOD;
            continue;
        }

        for(auto i : s[cur]){
            ct[i] = (ct[i] + ct[cur]) % MOD;
            ru[i]--;
            if(!ru[i]) q.push(i);
        }
    }

    printf("%d
", ans);

    return 0;
}

---

 2.杂务

 (这题有一种bug解法,见洛谷题解区,这里不讲)

如果将杂务A记录为杂务B的准备工作记录为有向边A→B,由于杂务k的准备工作总是在1~k-1中,最终将构造出一个有向无环图.

杂务总是在它的准备工作全都完成后可以进行,这意味着一项杂务的最早完成时间是其准备工作最早完成时间中的最大值与完成该杂务所需时间之和,这是个状态转移方程:

Time[i] = max{ Time[j] } + len[i],存在边 j → i .

进行这样的状态转移意味着转移到某个点总是需要其所有父节点都已经被遍历,这还是拓扑排序.

先从入度为0的点入手开始处理(处理后的点不再算入其子节点入度),并将每次处理后发现的新的入度变为0的点加入到待处理的队列中.

(这份代码是逐个检查父节点是否已处理的,劣于上述方法)

#include <algorithm>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <vector>
using namespace std;

vector<int> s[10010], f[10010];
int n, len[10010], ans[100010], deg[100010];

int main() {
    // freopen("in.txt", "r", stdin);
    cin >> n;
    for (int i = 1; i <= n; i++) {
        ans[i] = 0x7FFFFFFF;
        int t;
        cin >> t >> len[i];
        while(cin >> t && t){
            s[t].push_back(i);
            f[i].push_back(t);
            deg[i]++;
        }
    }
    for(int i = 1; i <= n; i++) sort(s[i].begin(), s[i].end());

    ans[1] = len[1];
    for(int i = 1; i <= n; i++){
        for(auto j : s[i]){
            deg[j]--;
            if(!deg[j]){
                int big = -1;
                for(auto k : f[j]) big = max(big, ans[k]);
                ans[j] = len[j] + big;
            }
        }
    }

    int tmp = 0;
    for(int i = 1; i <= n; i++) tmp = max(tmp, ans[i]);
    printf("%d
", tmp);

    return 0;
}

---

 3.最长路

这是一个有向无环图(DAG).

既然起点和终点都已知,我就直接写了个以1为起点的bfs,不过这是一个带权图,第一次到达某个点时并不能保证这时得到的就是到达该点的最值距离,但如果不是,说明还有其它到达该点的路径,到那时候在此更新答案为时不晚,只是复杂度变高了.可以AC.

写完了才知道这叫SPFA,百度查出来一堆争议,先不管那些.

#include <algorithm>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <queue>
#include <vector>
using namespace std;

typedef pair<int, int> P;        // 看了后面的代码你会发现完全没必要使用pair,队列处理int就可以了
queue<P> q;
vector<P> s[1510];
int n, m, dist[1510];

int main(){
    // freopen("in.txt", "r", stdin);
    scanf("%d%d", &n, &m);
    while(m--){
        int u, v, w;
        scanf("%d%d%d", &u, &v, &w);
        s[u].push_back(make_pair(v, w));
    }
    q.push(make_pair(1, 0));

    while(!q.empty()){
        P cur = q.front();
        q.pop();

        for(auto i : s[cur.first])
            if(dist[i.first] < i.second + cur.second){
                dist[i.first] = i.second + cur.second;
                q.push(make_pair(i.first, dist[i.first]));    // 这里看出来pair多此一举
            }
    }

    printf("%d
", dist[n] ? dist[n] : -1);

    return 0;
}