2019 ICPC 南昌 (C E G L)

https://vjudge.net/contest/440183#overview

当天过了两道,一个签到的简单模拟(L),还有一个最大生成树(E).

C - And and Pair

给出长度为1e5的01串,要求满足:

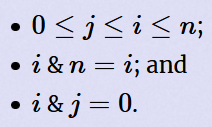
 的(i,j)有多少对.

数学题,运用排列组合,推导过程里出现了二项式定理.

#include <algorithm>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <string>
using namespace std;
#define M 1000000007

string s;

long long ksm(long long b, long long p){
    long long ans = 1 % M;
    while(p){
        if(p & 1) ans = (long long)ans * b % M;
        b = (long long)b * b % M;
        p >>= 1;
    }
    return ans;
}

void solve(){
    cin >> s;
    reverse(s.begin(), s.end());
    long long ct1 = 0, ct0 = 0, ans = 0;
    for(auto i = s.begin(); i != s.end(); i++){
        auto c = *i;
        if(c == '1') {
            ans = (ans + ksm(3, ct1) * ksm(2, ct0)) % M;
            ct1++;
        }else ct0++;
    }
    printf("%lld
", ans + 1);
}

int main(){
    int t;
    scanf("%d", &t);
    while(t--) solve();   

    return 0;
}

 

E - Bob's Problem

最小(大)生成树,这种题目再怎么变好像都不是很难.

可以看出来加黑边没有任何坏处,所以直接全部加上,在此后得到的图上使用Kruskal,首先检验一下在k条白边内能否得到生成树,如果不能则输出-1,否则把树生成出来,然后从大到小把剩下的(如果有)边的值加上去.

#include <algorithm>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <queue>
using namespace std;

struct E{
    int from, to, wei, col;
    bool operator<(const E&other) const {return wei > other.wei;}
};
vector<E> e;
queue<int> q;
int n, m, k, fa[50010];

int get(int x) {return fa[x] == x ? x : fa[x] = get(fa[x]);}
void merge(int x, int y) {fa[get(x)] = fa[get(y)];}

void solve(){
    e.clear();
    while(!q.empty()) q.pop();
    scanf("%d%d%d", &n, &m, &k);
    for(int i = 1; i <= n; i++) fa[i] = i;
    long long ans = 0;
    while(m--){
        int u, v, w, c;
        scanf("%d%d%d%d", &u, &v, &w, &c);
        if(c == 0) {
            ans += w;
            merge(u, v);
        }else e.push_back({u, v, w, c});
    }
    sort(e.begin(), e.end());

    for(auto i = e.begin();k && i != e.end(); i++){
        auto cur = *i;
        if(get(cur.from) == get(cur.to)) q.push(cur.wei);
        else {
            merge(cur.from, cur.to);
            ans += cur.wei;
            k--;
        }
    }
    while(k-- && !q.empty()){
        ans += q.front();
        q.pop();
    }

    int ct = 0;
    for(int i = 1; i <= n; i++) if(fa[i] == i) ct++;
    if(ct == 1)
        printf("%lld
", ans);
    else
        puts("-1");
}

int main(){
    int t;
    scanf("%d", &t);
    while(t--) solve();   

    return 0;
}

G - Eating Plan

 将一个1~n的排列中的每个数转化为其对应的阶乘,得到一个序列.要求从中选择连续的一段,使得该段上的值的和对998857459取模后不小于给定的k(序列不变,对k进行m次询问).

n,m均为1e5.

可以想一想,如果不考虑序列内都是排列的阶乘这一性质,即序列中的数是无规律的,这一问题可能没有合理的时间复杂度的求解方法.

答案是,这个模数有猫腻.

如果用下面的方法分解一下998857459的因数:

#include <algorithm>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <set>
using namespace std;

int t = 998857459;
set<int> s;

int main(){
    for(int i = 2; i < 10000000; i++)
        while(t % i == 0) t /= i, s.insert(i);
    for(auto i : s) cout << i << endl;

    return 0;
}

会得到

461 
773 
2803

这意味着对于一个x>=2803,x!=1*2*3*...*461*...*773*...*2803*...*x,其对998857459取模后为0.

因此不管n有多大,最多有2803个值不是0,对于为0的数是很好处理的.

这种题目算是用来开眼界吧.

#include <algorithm>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <queue>
using namespace std;

struct E{
    int from, to, wei, col;
    bool operator<(const E&other) const {return wei > other.wei;}
};
vector<E> e;
queue<int> q;
int n, m, k, fa[50010];

int get(int x) {return fa[x] == x ? x : fa[x] = get(fa[x]);}
void merge(int x, int y) {fa[get(x)] = fa[get(y)];}

void solve(){
    e.clear();
    while(!q.empty()) q.pop();
    scanf("%d%d%d", &n, &m, &k);
    for(int i = 1; i <= n; i++) fa[i] = i;
    long long ans = 0;
    while(m--){
        int u, v, w, c;
        scanf("%d%d%d%d", &u, &v, &w, &c);
        if(c == 0) {
            ans += w;
            merge(u, v);
        }else e.push_back({u, v, w, c});
    }
    sort(e.begin(), e.end());

    for(auto i = e.begin();k && i != e.end(); i++){
        auto cur = *i;
        if(get(cur.from) == get(cur.to)) q.push(cur.wei);
        else {
            merge(cur.from, cur.to);
            ans += cur.wei;
            k--;
        }
    }
    while(k-- && !q.empty()){
        ans += q.front();
        q.pop();
    }

    int ct = 0;
    for(int i = 1; i <= n; i++) if(fa[i] == i) ct++;
    if(ct == 1)
        printf("%lld
", ans);
    else
        puts("-1");
}

int main(){
    int t;
    scanf("%d", &t);
    while(t--) solve();   

    return 0;
}

L - Who is the Champion

签到,排个序就好.

#include <algorithm>
#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;

int n, G[110][110];
struct T{
    int num, dif, sco;
    bool operator<(const T& other) const {if(sco != other.sco) return sco > other.sco; return dif > other.dif;}
}t[110];

int main(){
    scanf("%d", &n);
    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= n; j++){
            scanf("%d", &G[i][j]);
            t[i].dif += G[i][j];
            t[j].dif -= G[i][j];
            t[i].num = i;
        }

    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= n; j++){
            if(G[i][j] > G[j][i]) t[i].sco += 3;
            else if(G[i][j] == G[j][i]) t[i].sco += 1;
        }

    sort(t + 1, t + 1 + n);
    if(t[1].sco == t[2].sco && t[1].dif == t[2].dif) puts("play-offs");
    else printf("%d
", t[1].num);

    return 0;
}