BST调了一天,最后遍历参数错了,没药救了……
本文所有代码均使用数组+结构体,不使用指针!
前言——BST是啥
BST 二叉搜索树是基于二叉树的一种树,一种特殊的二叉树。
二叉搜索树要么是一颗空树,要么满足一下特点(性质)的二叉树:
- 它的左子树要么为空,要么它(左子树)的所有节点均小于它的根节点。
- 它的右子树要么为空,要么它(右子树)的所有节点均大于它的根节点。
- 它的左、右子树也分别是二叉搜索树。
直观的说,如果中序遍历一棵二叉搜索树,则会产生一个有序数列。
如: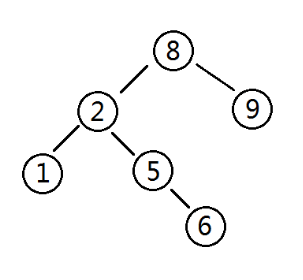
,中序遍历会产生序列:1 2 5 6 8 9
No.1——算法复杂度分析
二叉搜索树是"排过序"的二叉树,并非"用于排序"的二叉树。
它的优势在于"有序性",而且其插入和查找的时间复杂度均为(O(h)),一般情况下(h=O(log_{2}n)),n代表节点数,h代表树的高度。堆的插入算法虽然时间复杂度为(O(log_{2}n)),但并不具有有序性。
No.2——使用范围
对比上述的的分析,发现BST的特点是:
- 有序
- 插入、查找等算法高效
因此,BST使用范围是:要经常对有序数列进行"动态的"插入或查找等工作。
No.3——基本操作
BST的基本操作很多,一时半会也讲不过来,就从易到难的讲吧。
No.3-1——三种遍历方式
BST的遍历与二叉树和树一样,有三种:先序遍历、中序遍历、后续遍历。
三种遍历的方式:
- 先序遍历:根→左→右 (DLR)
- 中序遍历:左→根→右 (LDR) (结合定义,想一想,为什么中序遍历就是有序的？？)
- 后续遍历:左→右→根 (LRD)
想必大家都知道了吧,上代码。
/*========遍历========*/
void bl(int how,int now)
{
if(how==1){ //先序遍历
cout<<a[now].data<<" ";
if(a[now].l!=-1)
bl(1,a[now].l);
if(a[now].r!=-1)
bl(1,a[now].r);
}
if(how==2){ //中序遍历
if(a[now].l!=-1)
bl(2,a[now].l);
cout<<a[now].data<<" ";
if(a[now].r!=-1)
bl(2,a[now].r);
}
if(how==3){ //后续遍历
if(a[now].l!=-1)
bl(3,a[now].l);
if(a[now].r!=-1)
bl(3,a[now].r);
cout<<a[now].data<<" ";
}
}
No.3-2——建树与插入
强烈建议使用父亲孩子表示法!!!
所谓建树,就是构建一颗树,建树的时候必然涉及到插入。
也没有什么好说的,根据定义走,他怎么说,你怎么做。
- 第一个为根节点
- 比根大,往右对比
- 比根小,往左对比
- 如果当前为空,插入成功。
就这四步,代码来了
/*========插入========*/
void into(int sum,int now,int tot)
{
if(sum<a[now].data)
if(a[now].l!=-1)
into(sum,a[now].l,tot);
else {
a[now].l=tot;
a[a[now].l].data=sum;
a[a[now].l].fa=now;
}
else if(sum>a[now].data)
if(a[now].r!=-1)
into(sum,a[now].r,tot);
else {
a[now].r=tot;
a[a[now].r].data=sum;
a[a[now].r].fa=now;
}
}
/*========构建========*/
void init()
{
cin>>n;
int x,tot;
for(tot=1;tot<=n;tot++){
scanf("%d",&x);
if(tot==1)
a[tot].data=x;
else
into(x,1,tot);
}
}
No.3-3——查找
查找也是二叉搜索树必不可少的一个操作,我这里find()返回了是第几个数,方便删除。
实现很简单,只用熟练掌握二叉搜索树的性质,便可轻易打出以下代码:
/*========查找========*/
int find(int now,int sum)
{
cout<<now<<endl;
if(a[now].data==sum) return now;
if(sum<a[now].data)
if(a[now].l!=-1) return find(a[now].l,sum);
else return 0;
else if(sum>a[now].data)
if(a[now].r!=-1) return find(a[now].r,sum);
else return 0;
}
void init2()
{
cin>>n;
int i,x;
for(i=1;i<=n;i++){
cin>>x;
if(find(ROOT,x)) printf("Yes
");
else printf("No
");
}
}
No.3-4——求前驱后继
前驱后继就是在中序遍历时他的前一个与后一个,如图:
如图,八的前驱是六,后继是九。
这太简单了!
放到树上说,前驱就是该节点左儿子的最右节点,后继则是该节点右儿子的最左节点。
放一个前驱的代码,后继自己推!
/*========前驱========*/
int pred(int now)
{
if(a[now].r!=-1) return pred(a[now].r);
else return now;
}
No.3-5——删除
本操作有一定难度,请务必弄懂
删除要分一些情况讨论,见下:
- 没有孩子
- 只有一个孩子
3-1. 有两个孩子
3-2. 删除根
第一种情况好办,删掉就行了。
第二种情况也行,删掉后接上左/右孩子。
第三种情况有些复杂,需要用到前驱/后继(用哪个没有一定要求),用它的前驱/后继代替它,同时删除(一个递归过程,又一次调用删除函数)它的前驱/后继。
看一组图吧(有点大):
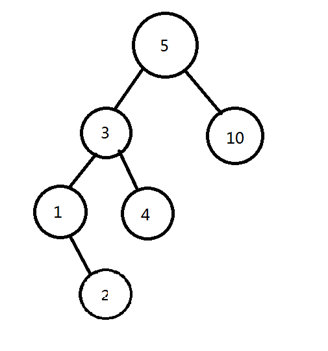这是一颗二叉搜索树,我们要删掉3。
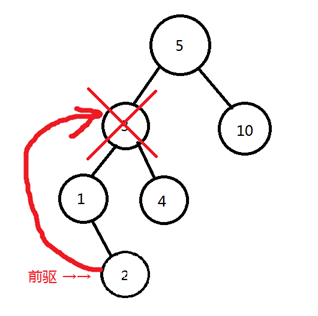找到前驱。
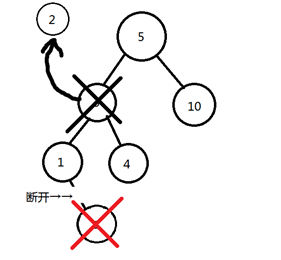替换。
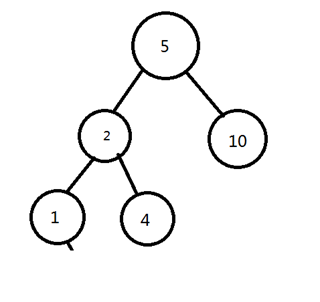最后变成这个样子。
最后讲一讲如何删根节点,其实与其他删除差不多,只需在开个ROOT变量存储根是谁就行了(根默认为1)
因为一些原因,不放代码。(其实是我太懒了)
No.4——写在最后
其实个人认为二叉搜索树的实用价值不大,主要用于练手与预备知识,比方说Treap、平衡树、堆……都需要用到二叉搜索树的性质。
综合代码算了,删除你们自己打吧!