The main road in Bytecity is a straight line from south to north. Conveniently, there are coordinates measured in meters from the southernmost building in north direction.
At some points on the road there are n friends, and i-th of them is standing at the point xi meters and can move with any speed no greater than vi meters per second in any of the two directions along the road: south or north.
You are to compute the minimum time needed to gather all the n friends at some point on the road. Note that the point they meet at doesn't need to have integer coordinate.
The first line contains single integer n (2 ≤ n ≤ 60 000) — the number of friends.
The second line contains n integers x1, x2, ..., xn (1 ≤ xi ≤ 109) — the current coordinates of the friends, in meters.
The third line contains n integers v1, v2, ..., vn (1 ≤ vi ≤ 109) — the maximum speeds of the friends, in meters per second.
Print the minimum time (in seconds) needed for all the n friends to meet at some point on the road.
Your answer will be considered correct, if its absolute or relative error isn't greater than 10 - 6. Formally, let your answer be a, while jury's answer be b. Your answer will be considered correct if 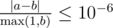 holds.
holds.
3
7 1 3
1 2 1
2.000000000000
4
5 10 3 2
2 3 2 4
1.400000000000
In the first sample, all friends can gather at the point 5 within 2 seconds. In order to achieve this, the first friend should go south all the time at his maximum speed, while the second and the third friends should go north at their maximum speeds.
题目链接:http://codeforces.com/contest/782/problem/B
题意:坐标上有n个点的坐标x[i],现在每个点以不超过v[i]的速度聚集于一点,问最少的时间。
思路:单调函数用二分,凹函数(或者凸函数)用三分,即二分再二分。[L,R] mid=(L+r)/2 mm=(mid+R)/2 if mid更靠近极点,R=mm;else L=mid;
代码:

#include<iostream> #include<cstdio> #include<cmath> #include<cstring> #include<algorithm> using namespace std; typedef long long ll; const int MAXN=6e4+100; double x[MAXN],v[MAXN]; bool eps(double L,double R) { if(fabs(L-R)<=1e-6) return false; else return true; } int main() { int n; scanf("%d",&n); double L=1e9,R=0; for(int i=1; i<=n; i++) { scanf("%lf",&x[i]); L=min(L,x[i]); R=max(R,x[i]); } for(int i=1; i<=n; i++) scanf("%lf",&v[i]); double ans=0; while(eps(L,R)) { double mid=(L+R)/2; double mm=(mid+R)/2; double t1=0,t2=0; for(int i=1; i<=n; i++) { t1=max(t1,fabs(x[i]-mid)/v[i]); t2=max(t2,fabs(x[i]-mm)/v[i]); } if(t1<=t2) R=mm,ans=t1; else L=mid; } printf("%.6f ",ans); return 0; }
