Description

Input

Output

HINT
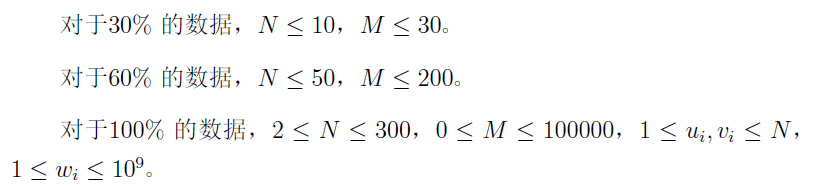
题解:
一种很直观的想法是通过矩阵生成树求树形图方法数ans以及不包含某一条边i的树形图方法数ans[i],则答案为Σ(ans-ans[i])*w[i]。
对于树形图,矩阵生成树的建立方法是:将有向边(u,v)加入,即inc(A[u,u])(如果是要求n能够走到所有点则inc(A[v,v])),dec(A[u,v])。
删去第n行与第n列后,求行列式(即m[n,n],m为余子式矩阵)。
对于要删去某条边情况下的m[n,n],只要修改矩阵的两项,再求m[n,n]。因为总要删去第n行与第n列,所以只要保留(n-1)*(n-1)的矩阵,每次求整个矩阵的行列式即可。
但是这样做肯定会TLE,考虑使用伴随矩阵去优化。
有公式:![]()
其中,A为原矩阵,A*为A的伴随矩阵,即A的代数余子式矩阵cof A的转置。(cof A[i,j]=(-1)^(i+j)*m[i,j])
我们通过高斯消元求行列式以及矩阵求逆,计算出A*,转置得到cof A。
对矩阵行展开求行列式的公式是: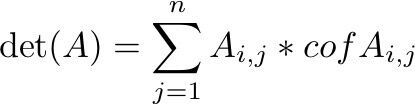
当删去一条边时,只修改了A[u,u]与A[u,v],它们都在第u行,所以cof A的第u行不变。
我们可以按第u行展开,O(n)求解。多预处理一些东西,甚至可以O(1)求解。
代码:

1 #include<bits/stdc++.h> 2 using namespace std; 3 const int mo=1000000007; 4 int n,m; 5 int ksm(int xx,int yy) 6 { 7 int zz=1; 8 while(yy) 9 { 10 if(yy&1)zz=(1ll*xx*zz)%mo; 11 yy>>=1; xx=(1ll*xx*xx)%mo; 12 } 13 return zz; 14 } 15 int t[301][601]; 16 struct matrix 17 { 18 int a[301][601]; 19 void cheng(matrix &b) //矩阵乘法 20 { 21 for(int i=1;i<=n;i++) 22 for(int j=1;j<=n;j++) 23 { 24 t[i][j]=0; 25 for(int k=1;k<=n;k++)t[i][j]=(1ll*a[i][k]*b.a[k][j]+t[i][j])%mo; 26 } 27 for(int i=1;i<=n;i++) 28 for(int j=1;j<=n;j++)a[i][j]=t[i][j]; 29 } 30 void hswap(int i,int j) //矩阵行交换 31 { 32 for(int k=1;k<=2*n;k++){ int t=a[i][k]; a[i][k]=a[j][k]; a[j][k]=t; } 33 } 34 void hadd(int i,int j,int l) //矩阵行之间加减 35 { 36 for(int k=1;k<=2*n;k++)a[j][k]=(1ll*l*a[i][k]+a[j][k])%mo; 37 } 38 void qiuni() //矩阵求逆 39 { 40 int flag=0; 41 for(int i=1;i<=n;i++)a[i][i+n]=1; 42 for(int i=1;i<=n;i++) 43 { 44 int j=i; while((j<=n)and(a[j][i]==0))j++; 45 if(j>n){ flag=1; break; } 46 if(i!=j)hswap(i,j); 47 for(int j=i+1;j<=n;j++)if(a[j][i]!=0) 48 { 49 int xx=(1ll*a[j][i]*ksm(a[i][i],mo-2))%mo; 50 hadd(i,j,(-xx)%mo); 51 } 52 } 53 if(flag==1){ for(int i=1;i<=n;i++)for(int j=1;j<=2*n;j++)a[i][j]=0; return; } 54 for(int i=n;i>=1;i--) 55 { 56 int xx=ksm(a[i][i],mo-2); hadd(i,i,(xx-1)%mo); 57 for(int j=1;j<i;j++)if(a[j][i]!=0)hadd(i,j,(-a[j][i])%mo); 58 } 59 for(int i=1;i<=n;i++) 60 for(int j=1;j<=n;j++){ a[i][j]=a[i][j+n]; a[i][j+n]=0; } 61 } 62 int det() //求矩阵行列式 63 { 64 int ans=1; 65 for(int i=1;i<=n;i++) 66 for(int j=1;j<=n;j++)t[i][j]=a[i][j]; 67 for(int i=1;i<=n;i++) 68 { 69 int j=i; while((j<=n)and(a[j][i]==0))j++; 70 if(j>n)break; 71 if(i!=j)hswap(i,j),ans=-ans; 72 for(int j=i+1;j<=n;j++)if(a[j][i]!=0) 73 { 74 int xx=(1ll*a[j][i]*ksm(a[i][i],mo-2))%mo; 75 hadd(i,j,(-xx)%mo); 76 } 77 } 78 for(int i=1;i<=n;i++)ans=(1ll*ans*a[i][i])%mo; 79 for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)a[i][j]=t[i][j]; 80 return ans; 81 } 82 void zhuanzhi() //矩阵转置 83 { 84 for(int i=1;i<=n;i++) 85 for(int j=1;j<i;j++){ int t=a[i][j]; a[i][j]=a[j][i]; a[j][i]=t; } 86 } 87 } x,y; 88 int b[100001][2],w[100001]; 89 int ans,ans2,tot; 90 int main() 91 { 92 freopen("calc.in","r",stdin); 93 freopen("calc.out","w",stdout); 94 scanf("%d%d",&n,&m); 95 for(int i=1;i<=m;i++)scanf("%d%d%d",&b[i][0],&b[i][1],&w[i]); 96 for(int i=1;i<=m;i++) 97 if(b[i][0]<n){ (x.a[b[i][0]][b[i][0]]+=1)%=mo; if(b[i][1]<n)(x.a[b[i][0]][b[i][1]]-=1)%=mo; } 98 n--; int ans=x.det(); 99 int ni=ksm(ans,mo-2); 100 for(int i=1;i<=n;i++) 101 for(int j=1;j<=n;j++)y.a[i][j]=(1ll*x.a[i][j]*ni)%mo; 102 y.qiuni(); y.zhuanzhi(); 103 for(int i=1;i<=m;i++) 104 if(b[i][0]<=n) 105 { 106 ans2=0; 107 (x.a[b[i][0]][b[i][0]]-=1)%=mo; if(b[i][1]<=n)(x.a[b[i][0]][b[i][1]]+=1)%=mo; 108 for(int j=1;j<=n;j++) 109 ans2=(1ll*x.a[b[i][0]][j]*y.a[b[i][0]][j]+ans2)%mo; 110 tot=(1ll*(ans-ans2)*w[i]+tot)%mo; 111 (x.a[b[i][0]][b[i][0]]+=1)%=mo; if(b[i][1]<=n)(x.a[b[i][0]][b[i][1]]-=1)%=mo; 112 } 113 tot=(tot+mo)%mo; 114 printf("%d ",tot); 115 }
