FFT也能用于一些特殊的字符串匹配与最小化问题。
Prob 1 : 给出模式串A与文本串B,两个串中只有26个大写字母与通配符'?'(即可以任意匹配一个字符),求A在B中的匹配数。要求以FFT为例给出上限为O(nlogn)的算法。
Prob 2 : 给出模式串A与文本串B,字符集很小,求A在B中的匹配数,允许有k个字符不同。要求以FFT为例给出上限为O(nlogn*|S|)的算法。
Prob 3 : 给出数列a和b,长度均为n,a可以顺时针转动但不能翻转,最小化sigma(ai*bi)。要求以FFT为例给出上限为O(nlogn)的算法。
不知道是什么东西的引导
我们先看看FFT干了什么,就是个卷积。
以数组a和b为例(这里下标从1开始),a有4位,b有8位,卷出的结果放在c数组中。
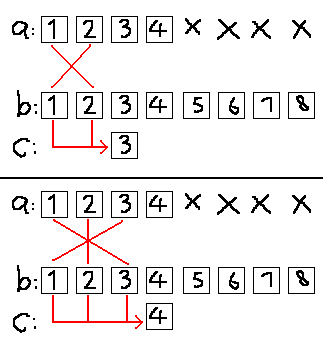
然而并没有什么用处。我们再往后看几位:
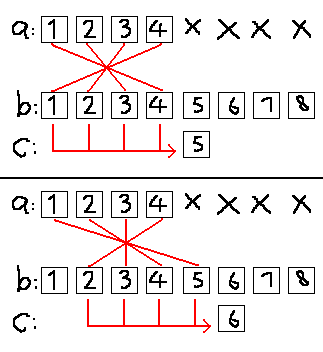
虽然FFT时会把a数组给自动补全,但从实际意义上来讲,只是整个a数组与b数组中四个数相乘放进c中。
不难发现,此时的下标就是一个“占位符”。
我们顺便把a数组反一反,就有:
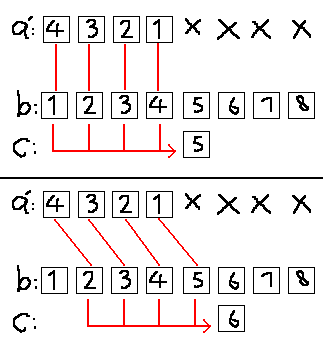
这样就有很好的性质了,c数组中从第5位开始,每往后一位就是整个a数组与b数组中连续的四位积的和。
同样可以拓展到更大的数组中,接下来的题目就要利用这个特点。
Prob 1
我们发现字符串的匹配很类似于上述图片中一位位算过去。
先不考虑通配符,只是普通的字符串匹配。定义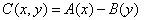 为A的第x位与B的第y位的匹配度。若C为0,则是匹配的。
为A的第x位与B的第y位的匹配度。若C为0,则是匹配的。
再定义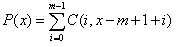 ,表示B字符串中以x为结尾,向前m-1位与A字符串的匹配度。我们天真地考虑若P为0,则是匹配的。
,表示B字符串中以x为结尾,向前m-1位与A字符串的匹配度。我们天真地考虑若P为0,则是匹配的。
但是C有正有负,因此一旦连续的几位的可重集是相同的,P的结果就为0。
所以在C上动手脚。干脆加个平方吧: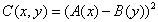
这样,
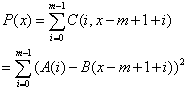
但还不能优化!因此我们又看了看上面的图,把A字符串反了过来。定义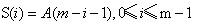
则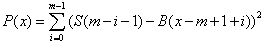
注意到(m-i-1)+(x-m+1+i)==x,有:
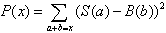
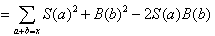
这样S与B做一遍卷积就行了。S与B的值取字符串的字符值就行了。
那带上通配符,只要有任何字符遇上“?”,C的值就必须是0。这样在原来P的式子中,后面乘上S与B中相应的第几位,若是“?”,给其赋值为0。则
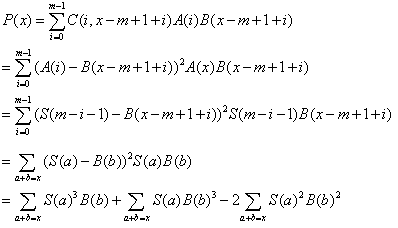
做三次FFT,加起来等于0的,即为匹配。

1 //源:https://www.luogu.org/problemnew/show/P4173 2 #include<bits/stdc++.h> 3 using namespace std; 4 const int maxn=1233333; 5 const double pi=3.1415926535898; 6 struct com 7 { 8 double a,b; 9 com(double A=0,double B=0){a=A,b=B;} 10 void operator=(com x){a=x.a,b=x.b;} 11 com operator+(com x){return com(a+x.a,b+x.b);} 12 com operator-(com x){return com(a-x.a,b-x.b);} 13 com operator*(com x){return com(a*x.a-b*x.b,a*x.b+b*x.a);} 14 com operator/(double d){return com(a/d,b/d);} 15 com operator*(double d){return com(a*d,b*d);} 16 }A[maxn],B[maxn],ans[maxn]; 17 int n,m,limit,r[maxn],len,g1[maxn],g2[maxn]; 18 char ch; 19 int re(int x) 20 { 21 int sum=0; 22 for(int i=0;i<len;++i) 23 { 24 sum=sum*2+x%2; 25 x/=2; 26 } 27 return sum; 28 } 29 void FFT(com*A,int g) 30 { 31 for(int i=0;i<limit;++i) 32 if(i<r[i])swap(A[i],A[r[i]]); 33 for(int i=2;i<=limit;i*=2) 34 { 35 com w(cos(2*pi/i),g*sin(2*pi/i)); 36 for(int j=0;j<limit/i;++j) 37 { 38 com d(1,0); 39 for(int k=0;k<i/2;++k) 40 { 41 com a=A[i*j+k],b=d*A[i*j+i/2+k]; 42 A[i*j+k]=a+b; 43 A[i*j+i/2+k]=a-b; 44 d=w*d; 45 } 46 } 47 } 48 } 49 void out(com*A) 50 { 51 for(int i=0;i<limit;++i)cout<<A[i].a<<' '; 52 cout<<endl; 53 } 54 void get(com*A,com*B) 55 { 56 FFT(A,1); 57 FFT(B,1); 58 for(int i=0;i<limit;++i)A[i]=A[i]*B[i]; 59 FFT(A,-1); 60 for(int i=0;i<limit;++i)A[i]=A[i]/limit; 61 } 62 int main() 63 { 64 ios::sync_with_stdio(false); 65 cin>>n>>m; 66 for(int i=n-1;i>=0;--i) 67 { 68 cin>>ch; 69 if(ch!='*') 70 { 71 int x=ch-'a'+1; 72 A[i]=g1[i]=x; 73 } 74 } 75 for(int i=0;i<m;++i) 76 { 77 cin>>ch; 78 if(ch!='*') 79 { 80 int x=ch-'a'+1; 81 g2[i]=x; 82 B[i]=x*x*x; 83 } 84 } 85 limit=1; 86 while(limit<n+m+1)limit*=2,++len; 87 for(int i=0;i<limit;++i)r[i]=re(i); 88 get(A,B); 89 for(int i=0;i<limit;++i)ans[i]=A[i]; 90 91 for(int i=limit-1;i>=0;--i)A[i]=g1[i]*g1[i]*g1[i]; 92 for(int i=0;i<limit;++i)B[i]=g2[i]; 93 get(A,B); 94 for(int i=0;i<limit;++i)ans[i]=ans[i]+A[i]; 95 96 for(int i=limit-1;i>=0;--i)A[i]=g1[i]*g1[i]; 97 for(int i=0;i<limit;++i)B[i]=g2[i]*g2[i]; 98 get(A,B); 99 for(int i=0;i<limit;++i)ans[i]=ans[i]-A[i]*2; 100 101 int tot=0; 102 for(int i=n-1;i<m;++i)if(int(ans[i].a+0.5)==0)++tot; 103 cout<<tot<<endl; 104 for(int i=n-1;i<m;++i)if(int(ans[i].a+0.5)==0)cout<<i-n+2<<' '; 105 cout<<endl; 106 return 0; 107 }
Prob 2
若字符只有’0'和'1'的呢?按照上面的做法,最后结果小于等于2的即为匹配(因为会有地方算两遍)。
再拓展一下,字符集多大就做几遍。最后的和加起来即可。
但由于一些奇妙的原因,至今我交不过去。只有网址。
其实随便哈希就能过了,SA也行。
https://www.luogu.org/problemnew/show/P3763
Prob 3
仍然是老套路。我们只要把其中某个数组的长度变为两倍,再重复写下前面的数就行了。
类似的题目:https://www.luogu.org/problemnew/show/P3723
最后,如果能用一些数据结构或方法来维护的话就别写FFT了。
