poj1330 lca 最近公共祖先问题学习笔记

首先推荐两个博客网址：

http://dongxicheng.org/structure/lca-rmq/

http://scturtle.is-programmer.com/posts/30055.html

[转]tarjan算法的步骤是(当dfs到节点u时):
1 在并查集中建立仅有u的集合,设置该集合的祖先为u
1 对u的每个孩子v:
   1.1 tarjan之
   1.2 合并v到父节点u的集合,确保集合的祖先是u
2 设置u为已遍历
3 处理关于u的查询,若查询(u,v)中的v已遍历过,则LCA(u,v)=v所在的集合的祖先
 
举例说明(非证明):

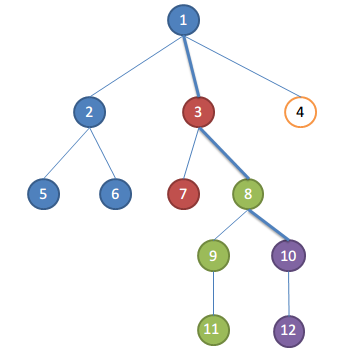
假设遍历完10的孩子,要处理关于10的请求了
取根节点到当前正在遍历的节点的路径为关键路径,即1-3-8-10
集合的祖先便是关键路径上距离集合最近的点
比如此时:
    1,2,5,6为一个集合,祖先为1,集合中点和10的LCA为1
    3,7为一个集合,祖先为3,集合中点和10的LCA为3
    8,9,11为一个集合,祖先为8,集合中点和10的LCA为8
    10,12为一个集合,祖先为10,集合中点和10的LCA为10
你看,集合的祖先便是LCA吧,所以第3步是正确的
道理很简单,LCA(u,v)便是根至u的路径上到节点v最近的点

为什么要用祖先而且每次合并集合后都要确保集合的祖先正确呢?
因为集合是用并查集实现的,为了提高速度,当然要平衡加路径压缩了,所以合并后谁是根就不确定了,所以要始终保持集合的根的祖先是正确的
关于查询和遍历孩子的顺序:
wikipedia上就是上文中的顺序,很多人的代码也是这个顺序
但是网上的很多讲解却是查询在前,遍历孩子在后,对比上文,会不会漏掉u和u的子孙之间的查询呢?
不会的
如果在刚dfs到u的时候就设置u为visited的话,本该回溯到u时解决的那些查询,在遍历孩子时就会解决掉了
这个顺序问题就是导致我头大看了很久这个算法的原因,也是絮絮叨叨写了本文的原因,希望没有理解错= =

对于这道题

题意：求最近公共祖先lca

下面是学来的tarjan代码

#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cmath>
#include <ctime>

using namespace std;

class Edge
{
    public:
    int    to;
    int    next;
}e[11000];

int    n,T,cnt;
int    f[11000],depth[11000],anc[11000],p[11000];
bool    visited[11000],In[11000];

inline    void    Add_edge(const int & x,const int & y)
{
    e[++cnt].to=y;
    e[cnt].next=p[x];
    p[x]=cnt;
    return ;
}

inline    int    get_anc(const int &x)
{
    return f[x]==x ? x:f[x]=get_anc(f[x]);
}

inline    void    Union(const int & x,const int & y)
{
    int    S,T;
    S=get_anc(x);
    T=get_anc(y);
    if(S==T)return ;
    if(depth[S]<=depth[T])
        f[S]=T,depth[S]+=depth[T];
    else
        f[T]=S,depth[T]+=depth[S];
    return ;
}

void    Dfs(const int &S,const int d)
{
    int    i;
    depth[S]=d;
    for(i=p[S];i;i=e[i].next)
    {
        Dfs(e[i].to,d+1);
    }

    return ;
}

int    Lca_tarjan(const int & s,const int & t,const int & u)
{
    int    i,temp;
    
    anc[u]=u;
    for(i=p[u];i;i=e[i].next)
    {
        temp=Lca_tarjan(s,t,e[i].to);
        if(temp)return temp;
        Union(u,e[i].to);
        anc[get_anc(u)]=u;
    }

    visited[u]=true;
    if(s==u&&visited[t])
        return anc[get_anc(t)];
    if(t==u&&visited[s])
        return anc[get_anc(s)];

    return 0;
}

inline    void    Init()
{
    cnt=0;
    memset(depth,0,sizeof(depth));
    memset(visited,0,sizeof(visited));
    memset(anc,0,sizeof(anc));
    memset(p,0,sizeof(p));
    memset(e,0,sizeof(e));
    memset(In,0,sizeof(In));

    for(int i=1;i<=n;++i)
    {
        f[i]=i;
    }

    return ;
}

int main()
{
    //freopen("1330.in","r",stdin);
    
    int    i,x,y,s,t,S;
    
    scanf("%d",&T);
    while(T--)
    {
        scanf("%d",&n);
        Init();
        for(i=1;i<n;++i)
        {
            scanf("%d%d",&x,&y);
            Add_edge(x,y);
            In[y]=true;
        }
        
        for(S=1;S<=n;++S)
            if(!In[S])break;

        scanf("%d%d",&s,&t);
        Dfs(S,1);
        printf("%d
",Lca_tarjan(s,t,S));
    }
    
    return 0;
}