1.梯度消失
根据链式法则,如果每一层神经元对上一层的输出的偏导乘上权重结果都小于1的话,那么即使这个结果是0.99,在经过足够多层传播之后,误差对输入层的偏导会趋于0。
这种情况会导致靠近输入层的隐含层神经元调整极小。
2.梯度膨胀
根据链式法则,如果每一层神经元对上一层的输出的偏导乘上权重结果都大于1的话,在经过足够多层传播之后,误差对输入层的偏导会趋于无穷大。
这种情况又会导致靠近输入层的隐含层神经元调整变动极大。
3. 梯度消失的原因详细解释
生物神经元似乎是用 Sigmoid(S 型)激活函数活动的,因此研究人员在很长一段时间内坚持 Sigmoid 函数。但事实证明,Relu 激活函数通常在 ANN 工作得更好。这是生物研究误导的例子之一。
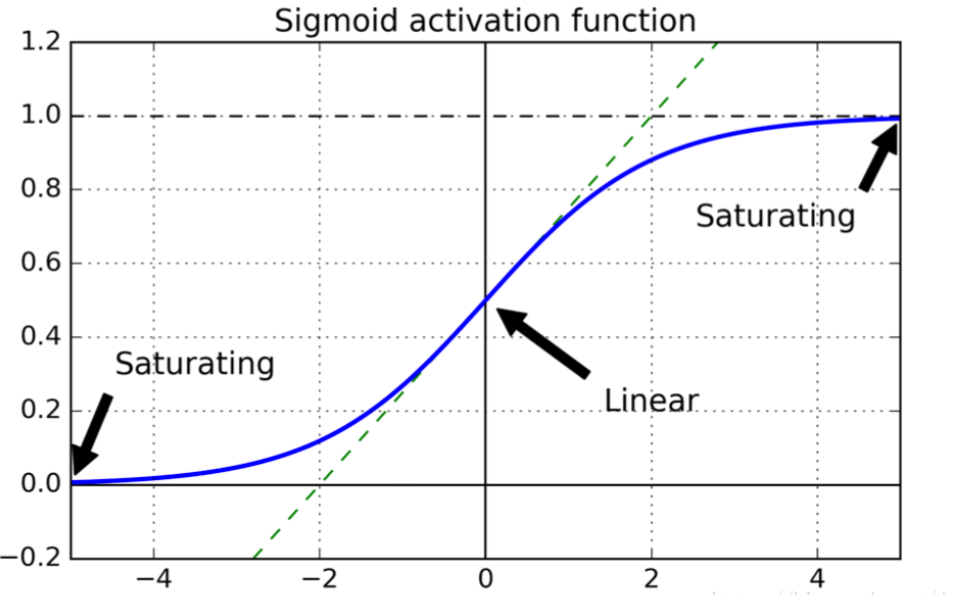
当神经网络有很多层,每个隐藏层都使用Sigmoid函数作为激励函数时,很容易引起梯度消失的问题
我们知道Sigmoid函数有一个缺点:当x较大或较小时,导数接近0;并且Sigmoid函数导数的最大值是0.25
我们将问题简单化来说明梯度消失问题,假设输入只有一个特征,没有偏置单元,每层只有一个神经元:

我们先进行前向传播,这里将Sigmoid激励函数写为s(x):
z1 = w1*x
a1 = s(z1)
z2 = w2*a1
a2 = s(z2)
...
zn = wn*an-1 (这里n-1是下标)
an = s(zn)
根据链式求导和反向传播,我们很容易得出,其中C是代价函数
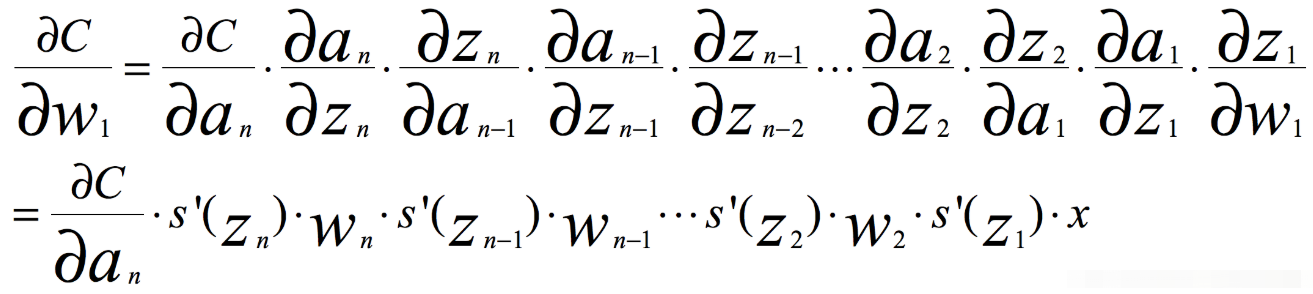
如果我们使用标准方法来初始化网络中的权重,那么会使用一个均值为0标准差为1的高斯分布。因此所有的权重通常会满足|wj|<1,而s‘是小于0.25的值,那么当神经网络特别深的时候,梯度呈指数级衰减,导数在每一层至少会被压缩为原来的1/4,当z值绝对值特别大时,导数趋于0,正是因为这两个原因,从输出层不断向输入层反向传播训练时,导数很容易逐渐变为0,使得权重和偏差参数无法被更新,导致神经网络无法被优化,训练永远不会收敛到良好的解决方案。 这被称为梯度消失问题。
4.梯度爆炸的原因
当我们将w初始化为一个较大的值时,例如>10的值,那么从输出层到输入层每一层都会有一个s‘(zn)*wn的增倍,当s‘(zn)为0.25时s‘(zn)*wn>2.5,同梯度消失类似,当神经网络很深时,梯度呈指数级增长,最后到输入时,梯度将会非常大,我们会得到一个非常大的权重更新,这就是梯度爆炸的问题,在循环神经网络中最为常见。
5.解决办法
梯度消失和梯度爆炸问题都是因为网络太深,网络权值更新不稳定造成的,本质上是因为梯度反向传播中的连乘效应。解决梯度消失、爆炸主要有以下几种方法:
(1) pre-training+fine-tunning
此方法来自Hinton在2006年发表的一篇论文,Hinton为了解决梯度的问题,提出采取无监督逐层训练方法,其基本思想是每次训练一层隐节点,训练时将上一层隐节点的输出作为输入,而本层隐节点的输出作为下一层隐节点的输入,此过程就是逐层“预训练”(pre-training);在预训练完成后,再对整个网络进行“微调”(fine-tunning)。此思想相当于是先寻找局部最优,然后整合起来寻找全局最优,此方法有一定的好处,但是目前应用的不是很多了。
(2) 梯度剪切:对梯度设定阈值
梯度剪切这个方案主要是针对梯度爆炸提出的,其思想是设置一个梯度剪切阈值,然后更新梯度的时候,如果梯度超过这个阈值,那么就将其强制限制在这个范围之内。这可以防止梯度爆炸。
(3) 权重正则化
另外一种解决梯度爆炸的手段是采用权重正则化(weithts regularization),正则化主要是通过对网络权重做正则来限制过拟合。如果发生梯度爆炸,那么权值就会变的非常大,反过来,通过正则化项来限制权重的大小,也可以在一定程度上防止梯度爆炸的发生。比较常见的是 L1 正则和 L2 正则,在各个深度框架中都有相应的API可以使用正则化。
(4) 选择relu等梯度大部分落在常数上的激活函数
relu函数的导数在正数部分是恒等于1的,因此在深层网络中使用relu激活函数就不会导致梯度消失和爆炸的问题。
(5) batch normalization
BN就是通过对每一层的输出规范为均值和方差一致的方法,消除了权重参数放大缩小带来的影响,进而解决梯度消失和爆炸的问题,或者可以理解为BN将输出从饱和区拉倒了非饱和区。
(6) 残差网络的捷径(shortcut)
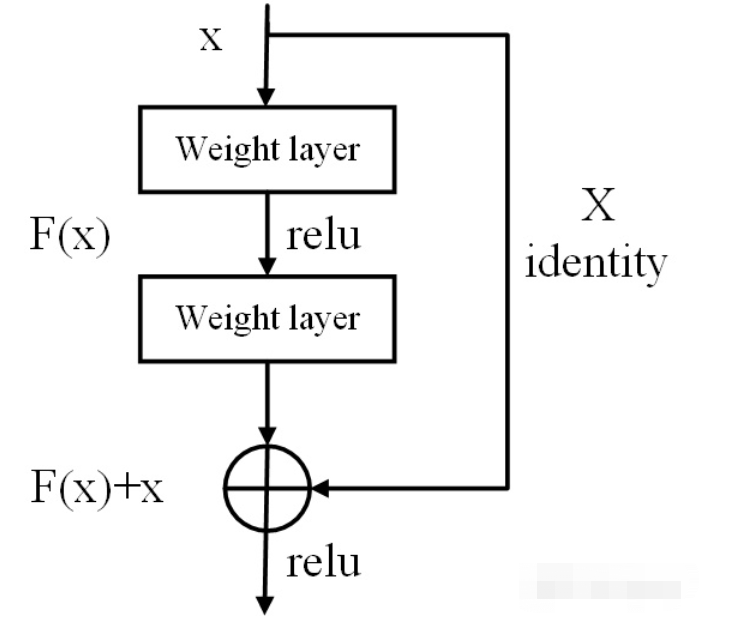
相比较于以前直来直去的网络结构,残差中有很多这样(如上图所示)的跨层连接结构,这样的结构在反向传播中具有很大的好处,可以避免梯度消失。
(7) LSTM的“门(gate)”结构
LSTM全称是长短期记忆网络(long-short term memory networks),LSTM的结构设计可以改善RNN中的梯度消失的问题。主要原因在于LSTM内部复杂的“门”(gates),如下图所示。
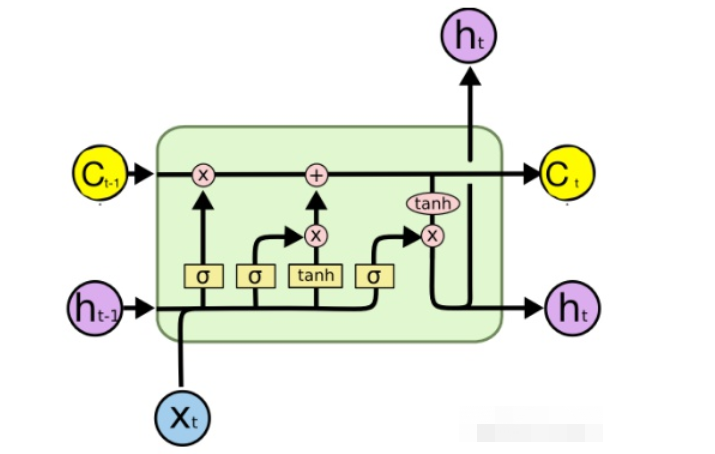
LSTM 通过它内部的“门”可以在接下来更新的时候“记住”前几次训练的”残留记忆“。
参考:
https://blog.csdn.net/junjun150013652/article/details/81274958