1.什么是直接选择排序?
直接选择排序(Straight Select Sort)是一种简单的排序方法,它的基本思想是:通过n-i次关键字之间的比较,从n-i+1个记录中选出关键字最小的记录,并和第i(1<=i<=n)个记录交换位置。
时间复杂度O(n2)
在排序时找到合适的关键字再做交换,并且只移动一次。
public class Test1{
public static void selectSort(int[] arr){
for(int i=0;i<arr.lenght;i++){
for(int j=i+1;j<arr.length;j++){
if(arr[i]>arr[j])//找到后面的元素比前面的小,就交换
swap(arr,i,j);
}
}
}
private static void swap(int[] arr,int x,int y){
int temp=arr[x];
arr[x]=arr[y];
arr[y]=temp;
}
public static void main(String[] args){
int[] a={4,2,1,6,0,-5,1};
int i;
selectSort(a);
for(i=0;i<7;i++)
System.out.print(a[i]);
}
}
栗子:排序算法中,比较次数与初始序列无关的排序方法有哪些?D
A.希尔排序
B.快速排序
C.堆排序
D.选择排序
2.堆排序
时间复杂度为O(nlogn),不稳定排序
堆是一个完全二叉树,树中每一个结点对应于原始数据的一个记录,并且每个结点应满足以下条件:非叶结点的数据大于或等于其左右孩子结点的数据(大顶堆)
若是按从小到大的顺序排序,则要求非叶结点的数据小于或等于其左右孩子结点的数据(小顶堆)
由堆的定义可以看出,其根结点为最大值,堆排序就是利用这一特性进行的。
堆的存储
一般都用数组来表示堆,i 结点的父结点下标就为(i – 1) / 2。它的左右子结点下标分别为2 * i + 1和2 * i + 2。如第0个结点左右子结点下标分别为1和2。
关于二叉树的一个性质:
如果对于一棵有n个结点的完全二叉树,对于任一结点 i有:
(1)如果i=1,则结点 i 是二叉树的根,无双亲;如果i>1,则其双亲是结点 i/2
(2)如果 2i>n,则结点 i 无左孩子(结点i是叶子结点),否则其左孩子是结点2i;
(3)如果2i+1>n,则结点 i 无右孩子,否则其右孩子是结点2i+1;
堆排序的大致过程包括两个阶段:
(1)将无序的数据构成堆(即用无序的数据生成满足堆定义的完全二叉树)
(2)利用堆排序(即用上一步生成的堆输出有序数据)
首先把无序数据构成堆
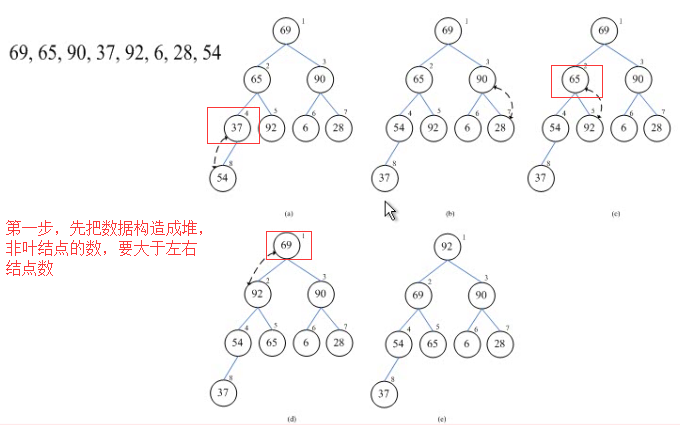
//构成堆
public static void HeapAdjust(int[] a,int s,int n){
int j,t;
while(2*s+1<n){//第s个结点有右子树
j=2*s+1;//左子树
if((j+1)<n){
if(a[j]<a[j+1])//如果左子树小于右子树,则需要比较右子树和s结点
j++;//序号加1,指向右子树
}
if(a[s]<a[j]){//如果s结点小于它的右子树,就进行交换
t=a[s];
a[s]=a[j];
a[j]=t;
s=j;//之前的堆被破坏了,需要调整
}
else{//比较左右孩子均大则堆未被破坏,不需要调整
break;
}
}
}
然后,每次将最后的数据(37)与最上面的数据(92)交换顺序,然后把把交换后的最上面的数据(92)输出,由于交换后肯定不满足堆了,就再重新构成堆。接下来接着进行交换。
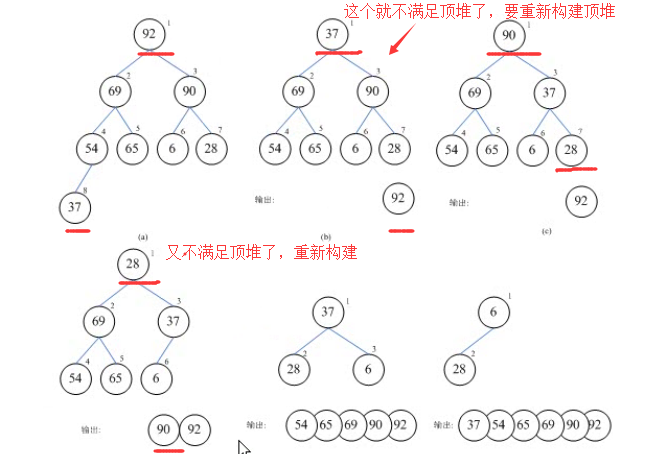
//堆排序
public static void HeapSort(int[] a,int n){
int t,i;
int j;
for(i=n/2-1;i>=0;i--){
HeapAdjust(a,i,n);//将a[0,n-1]构成大顶堆
}
for(i=n-1;i>0;i++){//将最后的一个,与第一个进行比较
t=a[0];
a[0]=a[i];
a[i]=t;
HeapAdjust(a,0,i);//将a[0]至a[i]重新进行调整
}
}