0、欢迎食用
- 作业题目:http://www.cnblogs.com/easteast/p/7469291.html
- github链接:https://github.com/H-BING/SoftwareEngineeringPractice/tree/master/sudoku
1、解题过程
-
第一版
- 看到题目第一眼的想法就是和做数独一样按规律填。最开始想的是一个数字一个数字进行符合要求的随机填空,思考了好一会觉得实现起来有点点复杂,没什么好的想法。然后就上网搜了一下各种数独生成的算法,找到看起来一个比较好实现的算法(实际上也很好实现hhh)。参考了里面的随机方式的思路:
- 写一个方法用于获取一个由1到9九个数随机排列的一维数组。
- 循环行(下标从0到8),将这个随机产生的一维数组作为当前行的内容,如果是第一行(行标为0),那么直接作为该行的内容。如果是其它行,则验证数据是否都符合条件。
- 如果符合条件,则再产生一个由1到9九个数随机排列的一维数组作为下一行的内容并验证数据是否可用。如果不符合条件,则……
- (其实我只看了第一行233)后面的做法就跟上面的不一样啦。
-
第二版
- 第一版改不下去,跟可靠人士交流后决定转投DFS回溯的怀抱。第一遍通过 DFS 生成一个数独终盘,之后的就通过回溯来生成。
主要想法就是一个个轮呗 0 0 对每个格子,判断1-9填入后是否符合数独要求。若符合要求则填入该数字并进行下一步搜索,不符合要求则换一个数字进行尝试。
- 第一版改不下去,跟可靠人士交流后决定转投DFS回溯的怀抱。第一遍通过 DFS 生成一个数独终盘,之后的就通过回溯来生成。
2、设计实现
-
第一版
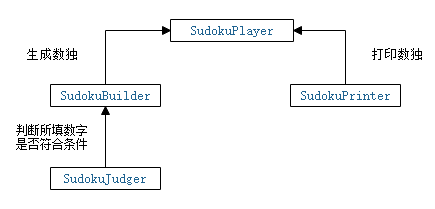
-
第二版
和第一版还是有些差别的。换了个生成类,由于算法的关系,改成了直接在生成类里面调用打印类。
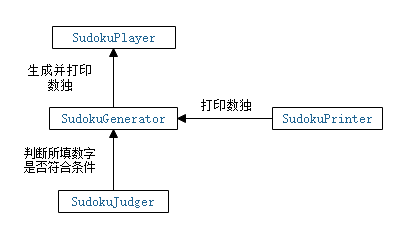
3、关键代码
-
第一版初稿
写的时候就能猜想到,整个项目的时间都耗在这里辣。不过先 make it work 咯。第一遍写除了一些知识点有点不清楚改了一小会,不考虑这些的话,还是全部一次性写完一次性成功的。非常满足。
主要想法就是生成一行1-9的随机排列,然后进行对应的验证,符合要求则拼接起来,不符合要求就重新生成直至找到满足要求的随机数列。
void SudokuBuilder::generateSudoku(int(&sudoku)[LENGTH][LENGTH]) {
initSudoku(sudoku);
SudokuJudger sudokuJuder;
// 第一行直接生成无须判断,故可直接拷贝。
memcpy(sudoku[0], randomArray(0), sizeof(int) * LENGTH);
for (int i = 1; i < LENGTH; i++) {
// 随机生成一行
int* temp = randomArray(i);
bool succeed = false;
while (!succeed) {
// 若随机生成的数组符合要求则继续,否则重新生成数组
if (sudokuJuder.judgeTempRow(i, tempArray, sudoku)) {
succeed = true;
} else {
tempArray = randomArray(i);
}
}
memcpy(sudoku[i], temp, sizeof(int) * LENGTH);
}
}
-
第一版终稿
主要是对上面函数中随机生成一行数组进行了修改。
while (!succeed) {
// 获取当前非法列
int column = sudokuJuder.judgeTempRow(i, tempArray, sudoku);
if (column == -1) {
succeed = true;
} else {
// 当前非法列与未被判断的数字进行随机交换
tempArray = randomArray(column, tempArray);
// 若当前列修改后仍为非法列则该行重新生成
int tempColumn = sudokuJuder.judgeTempRow(i, tempArray, sudoku);
if (tempColumn == column) {
tempArray = randomArray(i);
}
}
}
-
第二版初稿
因为实在改不来第一版算法,所以,我勇敢的决定换算法 0 0 并且据可靠人士亲测,DFS回溯效果不错。太久没写过了有点虚,网上找了一下模板。这个还是归纳的蛮清楚的,对着模板写一下,还是比较快就出来了,没有自己想象的那样艰难hhh。这算法效率比起原来那个提升了可真不止一点,回溯还能够保证所有生成的数独终盘一定不重复。开心。
目前判定条件暂时暴力搜索行+列+小矩阵,争取有时间优化。
其中DFS函数如下:
void SudokuGenerator::dfs(int(&sudoku)[LENGTH][LENGTH], int count, int(&n)) {
// 所要求生成终盘数已完成,可结束算法。
if (!n) {
return;
}
// 已生成一个符合要求的数独终盘,输出所得终盘。
if (count > 80) {
sudokuPrinter.printSudoku(sudoku);
--n;
return;
}
// 根据count值获得对应数独棋盘的坐标
int x = count / LENGTH, y = count % LENGTH;
// 若当前坐标已赋值则继续深搜
if (sudoku[x][y] != INITDATA) {
dfs(sudoku, count + 1, n);
}
for (int j = 1; j <= LENGTH; j++) {
// 回溯
if (sudokuJudger.checkRequirement(x, y, j, sudoku)) {
sudoku[x][y] = j;
dfs(sudoku, count + 1, n);
if (!n) {
return;
}
sudoku[x][y] = INITDATA;
}
}
}
- 发现邹老师一大早翻了一大波牌233
偷偷瞄到邹老师在别的博客下的评论dfs的易读性,写的时候就想当然觉得dfs默认深度优先搜索了 0 0
函数名已在github上更名为DepthFirstSearch了。
4、测试运行
- 简单玩了一下单元测试,不过还是不太清楚具体的应用 0 0 感觉像是验证性的测试。但在这个数独生成器项目中,好像没什么能测的诶 0 0 特别在我改了第二版之后貌似更没什么能用来进行单元测试的了。
- 运行成功截图
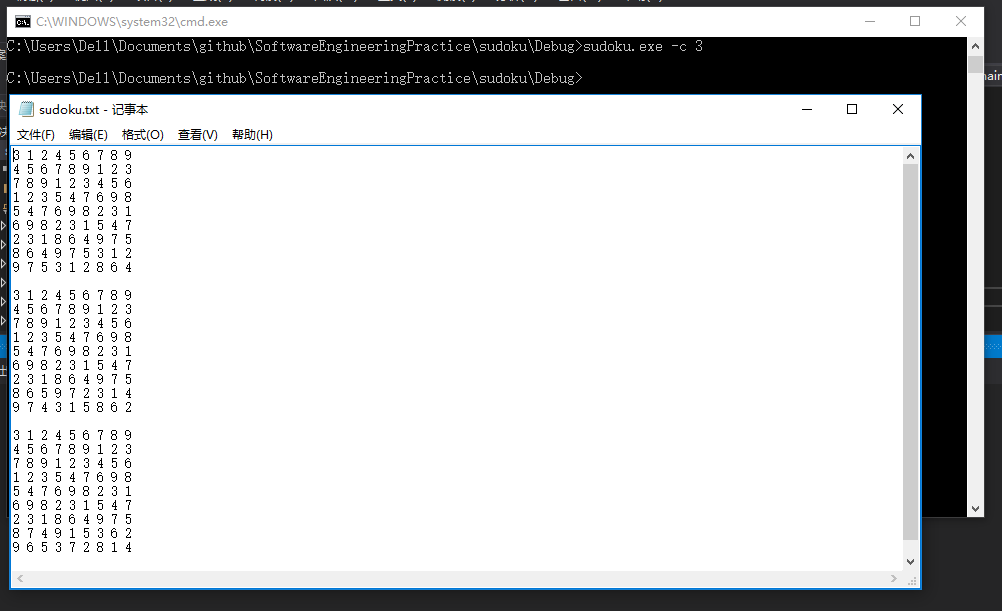
5、性能分析
-
第一版
- 第一版初稿:最最原始爆炸的性能。
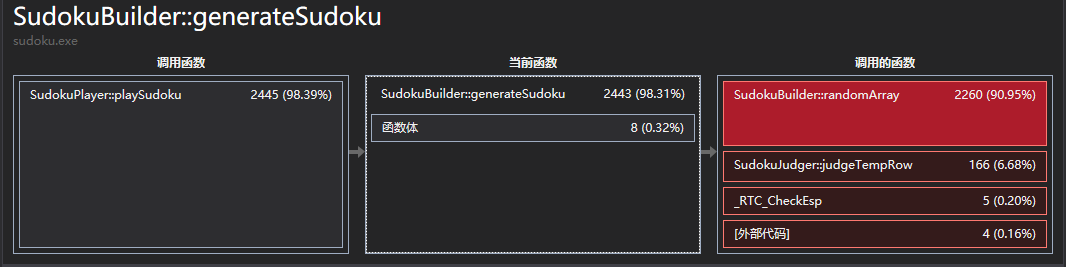
- 第一版终稿:
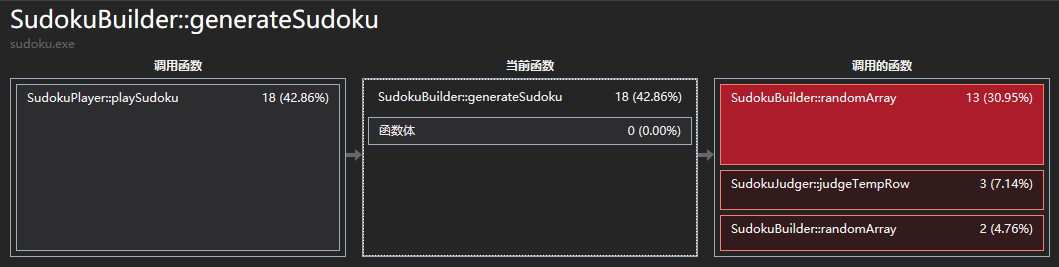 emmmm...看起来改进效果还是比较可观的。
emmmm...看起来改进效果还是比较可观的。 - 以上都是生成一次数独终盘的性能分析。如果生成终盘数目一多,就比较不好看了...折腾了很久还是不怎么会改,都没什么好的效果。不愧是随机算法,时间真的太随机了... 而且虽然重复的可能性也不太大,但是还是有可能存在重复的。
(之前忘记 push 到 Github 上面了,所以 Github上只有第一版的终稿 T T 后来把第一版的当作注释加进去了...啊函数有变化,算了就这样意思一下吧)
- 第一版初稿:最最原始爆炸的性能。
-
第二版
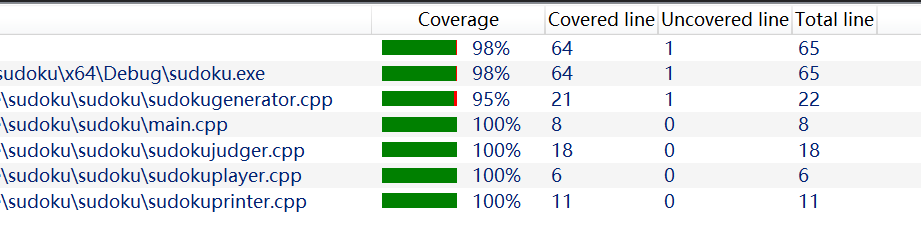
- 生成100w次的性能分析
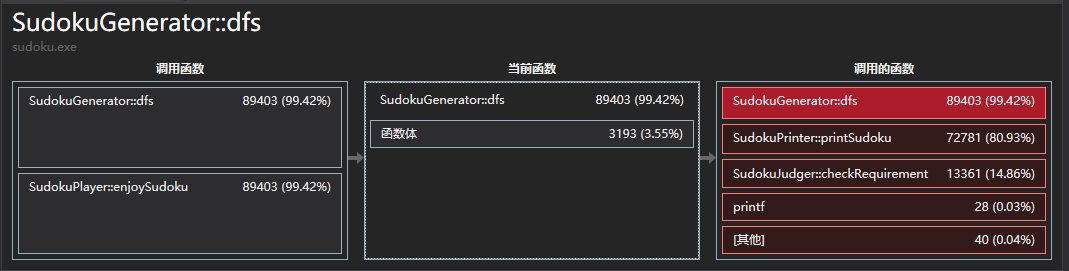 的确时间都花在输出上面了 0 0
的确时间都花在输出上面了 0 0 - 输出换
putchar()的100w
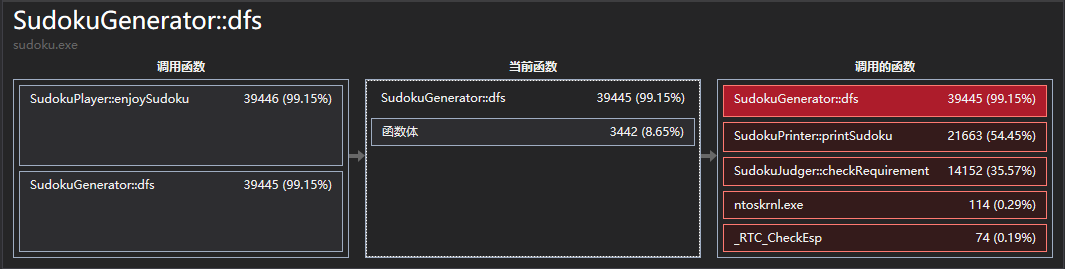 输出一改就可以看到判断emmmm...有时间再改吧。
输出一改就可以看到判断emmmm...有时间再改吧。
- 生成100w次的性能分析
6、PSP表格
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
|---|---|---|---|
| Planning | 计划 | 10 | 20 |
| · Estimate | · 估计这个任务需要多少时间 | 10 | 20 |
| Development | **开发 ** | 840 | **900 ** |
| · Analysis | · 需求分析 (包括学习新技术) | 180 | 320 |
| · Design Spec | · 生成设计文档 | - | - |
| · Design Review | · 设计复审 (和同事审核设计文档) | - | - |
| · Coding Standard | · 代码规范 (为目前的开发制定合适的规范) | - | - |
| · Design | · 具体设计 | 60 | 60 |
| · Coding | · 具体编码 | 180 | 80 |
| · Code Review | · 代码复审 | 60 | 60 |
| · Test | · 测试(自我测试,修改代码,提交修改) | 300 | 320 |
| Reporting | 报告 | 60 | 90 |
| · Test Report | · 测试报告 | - | - |
| · Size Measurement | · 计算工作量 | - | - |
| · Postmortem & Process Improvement Plan | · 事后总结, 并提出过程改进计划 | 60 | 90 |
| 合计 | 910 | 1010 |
- 做的时候就直接做了,没注意上面这些东西 0 0 都是大概估一下吧。下次会注意要求的 orz
7、参考资料
- git使用
http://www.cnblogs.com/schaepher/p/5561193.html
http://www.pfeng.org/archives/840
https://segmentfault.com/q/1010000000115900 - 数独终盘生成各类方法
https://my.oschina.net/wangmengjun/blog/781984
http://gundumw100.iteye.com/blog/760402
http://blog.csdn.net/nibiewuxuanze/article/details/47679927 - 性能分析
http://blog.csdn.net/luoweifu/article/details/51470998