TensorFlow实战（1）

神经网络的变量声明函数：tf.Variable()

初始化所有变量：

　　sess = tf.Session()

　　init_op = tf.global_variables_initializer()
　　sess.run(init_op)

对于交叉熵的理解：交叉熵是两个概率分布之间的距离。eg:

　　假如有个三分类问题，某个样例的正确答案是(1,0,0)。某模型经过softmax回归之后的预测答案是(0.5, 0.4, 0.1)那么这个预测和正确答案之间的交叉熵为：

　　　　H( (1,0,0),(0.5, 0.4, 0.1)) = - (1*log0.5 + 0*log0.4 + 0*log0,1) = 0.3

      如果另一个模型的预测是(0.8, 0.1, 0.1)，那么这个预测值和真实值之间的交叉熵是：

　　　　H( (1,0,0),(0.8, 0.1, 0.1)) = - (1*log0.8 + 0*log0.1 + 0*log0,1) = 0.1　　

　　从直观上，很明显知道第二个预测答案要明显优于第一个。通过交叉熵计算得到的结果也是一致的。

tensorflow输出一个变量的值，需要.eval()，eg:

with tf.Session() as sess:
    v = tf.constant([1.0, 2.0, 3.0])
    print(tf.clip_by_value(v, 2.5, 4.5).eval())

　　　输出：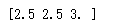

　　　否则，不加.eval()，输出：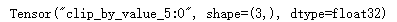

　　均方误差损失函数：

　　　　mse = tf.reduce_mean(tf.square(y_ - y))

　　交叉熵损失函数：

　　　　cross_entropy = -tf.reduce_mean(y_ *  tf.log(tf.clip_by_value(y, 1e-10, 1.0)))

　　　　注意上面的乘法符号"*"是点乘，TensorFlow中矩阵乘法用tf.matmul()函数完成。

关于L1正则化和L2正则化：

　　L1正则化会让参数变得更稀疏，会有更多的参数变为0，这样可以达到类似特征选取的功能。

　　而L2正则化不会，因为当参数很小，比如0.001，这个参数的平方基本上就可以忽略了，于是模型不会进一步将这个参数调整为0.

　　L1正则化的公式不可导，而L2正则化公式可导。因为在优化时需要计算损失函数的偏导数，所以对含有L2正则化损失函数的优化要更简洁。优化带L1正则化的

　　损失函数要更加复杂。

　　也可以将L1和L2正则化同时使用。

　　TensorFlow中L1和L2正则化函数：

　　　　tf.contrib.layers.l1_regularizer(lambda)(weights)

　　　　tf.contrib.layers.l2_regularizer(lambda)(weights)

　　　　其中，lambda是正则化程度，weights是网络权值。