【高手训练】【RMQ】奶牛排队

第一题由于过水，就没写awa

 

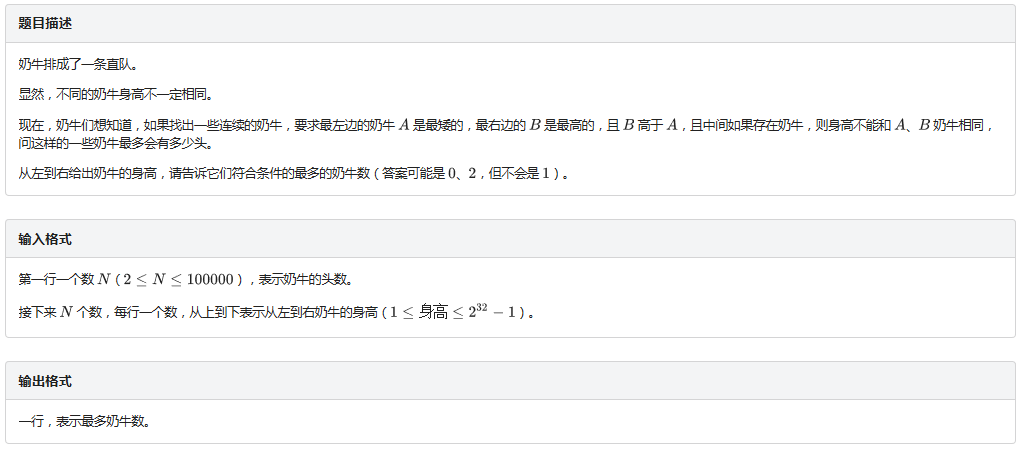
 大概就是这样了。
题意就是求一个最长的区间使得区间的左边是它的最小值，区间右边是他的最大值
第一个想法肯定是暴力枚举啦awa
但是这个是O(n^3)的，绝对的不可过awa

思考性质awa
发现我们枚举每个区间的左右端点，其实有大量的不合法的计算的
也就是没有用的枚举。

考虑怎么避开不合法区间的枚举。
那么就不要先考虑区间的范围。
先考虑合法性，也就是直接寻找符合条件的区间

考虑区间合法满足的条件。
首先，在一个区间中肯定是要满足最大值的位置max要在最小值的位置min后面的,即使max>min
可以发现，如果这个是存在的话，答案肯定是要尝试更新的。

如果不能更新的话，那么这个区间不代表就没有答案了。
所以我们还需要考虑一下在哪里会有答案。

对于一个max<min的区间
我们把他分为3个区间

 其中的max和min的位置就是最大值和最小值的位置。
因为max在min的后面，所以这整个大区间就不可能会有答案。
所以我们就用max为右边界，min为左边界，再次分割出两个区间。
这就是区间1和3的由来。
区间2是剩下的。
awa

然后对于中间有解的情况
就是这样的

 其中的区间2是已经有解的了，所以我们顶着min和max再次分割出两个区间。
就是区间1和3.
然后进行递归，就是答案了。
为了快速的统计最大值和最小值以及他们的位置，我们就用st表（这非常的显而易见）

然后就没了。

awa

code

#include<bits/stdc++.h>
#define ll long long
using namespace std;
ll n,m,a[100001];
ll maxn[100001][27],b[100001][27];
ll minn[100001][27],c[100001][27];
ll ans,logn[100001];
inline ll read()
{
    char c=getchar();ll a=0,b=1;
    for(;c<'0'||c>'9';c=getchar())if(c=='-')b=-1;
    for(;c>='0'&&c<='9';c=getchar())a=a*10+c-48;
    return a*b;
}
void get_maxx(ll x,ll y)//为了记录最大值和最小值的位置而被魔改的转移
{
    if(maxn[x][y-1]<maxn[x+(1<<y-1)][y-1])
    {
        maxn[x][y]=maxn[x+(1<<y-1)][y-1];
        b[x][y]=b[x+(1<<y-1)][y-1];
    }
    else
    {
        maxn[x][y]=maxn[x][y-1];
        b[x][y]=b[x][y-1];
    }
}
void get_minn(ll x,ll y)
{
    if(minn[x][y-1]<minn[x+(1<<y-1)][y-1])
    {
        minn[x][y]=minn[x][y-1];
        c[x][y]=c[x][y-1];
    }
    else
    {
        minn[x][y]=minn[x+(1<<y-1)][y-1];
        c[x][y]=c[x+(1<<y-1)][y-1];
    }
}
ll gax(ll l,ll r)
{
    ll s=logn[(-l)+r+1];
    if(maxn[l][s]<maxn[r-(1<<s)+1][s])return  b[r-(1<<s)+1][s];
    else return b[l][s];
}
ll gin(ll l,ll r)
{
    ll s=logn[(-l)+r+1];
    if(minn[l][s]>minn[r-(1<<s)+1][s])return c[r-(1<<s)+1][s];
    else return c[l][s];
}
void Find(ll l,ll r)
{
    ll x=gin(l,r),y=gax(l,r);
    if(x==y)return ;
    else
    {
        if(x<y)
        {
            ans=max(ans,(-x)+y+1);
            if(abs(x-l)>ans)Find(l,x-1);
            if(abs(r-y)>ans)Find(y+1,r);
        }
        else//x>y
        {
            if(abs(y-x)-1>ans)Find(y+1,x-1);
            if(abs(l-y)+1>ans)Find(l,y);
            if(abs(r-x)+1>ans)Find(x,r);
        }
    }    
}
int main()
{
    n=read();
    logn[0]=-1;
    for(ll i=1;i<=n;i++)
    a[i]=minn[i][0]=maxn[i][0]=read(),c[i][0]=b[i][0]=i,logn[i]=logn[i>>1]+1;
    for(ll j=1;j<=19;j++)
    {
        for(ll i=1;i+(1<<j)-1<=n;i++)
        {  
            get_maxx(i,j);
            get_minn(i,j);
        }
    }
    Find(1,n);
    cout<<ans<<endl; 
    return 0;
}