一、算法分析
1、 问题描述:
设G=<V, E>为一有向图,V={1,2,...,n},表示顶点编号;E为边的集合,图G中的每一条边(i, j)∈E,对应的距离值为w[i,j]。 顶点i,j间的距离定义为从i出发到j的最短路径长度。
目的:找出图G中每一个顶点到其他所有顶点的距离(有向图,即A到B与B到A的距离可能不一样)。
约定:若(i,j)∉E,则w[i,j]=∞;若i∈V,w[i,i]=0;
问题输入:表示待权有向图G=<V,E>的n*n矩阵W。
问题输出:对任意的i, j∈V,i到j的距离以及最短路径。
2、分析过程:
(1)设G中两个不同的顶点i,j∈V,p是从i到j其间仅经过{1,2,...,k}的最短路径。
(2)若p不经过顶点k,则p也是从i到j其间敬经过{1,2,...,k-1}的最短路径。
(3)若p经过顶点k,即p-->k-->j。将这两段分别记为p1,p2,则p1是从i到k其间仅经过{1,2,...,k-1}的最短路径,p2是k到j其间仅经过{1,2,...,k-1}的最短路径。(可由反证法证明)
个人理解:k为i到j的最短路径上的一个顶点,则i到k的最短路径+k到j的最短路径,与i到j的最短路径相同,其顶点必定相同。 判断顶点k是否需要加入最短路径,比较(2)与(3)的结果即可,若(2)<(3),则k点不加入最短路径。自底向上,逐个判断即可。
定义di,jk为i到j其间仅经过{1,2,...,k}的最短路径长度。递归表达式如下:
[d_{i,j}^{k}=
egin{cases}
w[i,j]& ext{k=0}\
minlbrace d_{i,j}^{k-1},d_{i,k}^{k-1} + d_{k,j}^{k-1}
brace & ext{1≤k≤n}\
end{cases}
]
顶点对的距离矩阵:
[D_k={d_{i,j}^k}_{(n,n)}
]
二、代码实现
最短路径:
pair floydWarshall(double *w, int n)
{
// 使用一维数组存储图的矩阵(邻接矩阵)
double *d = (double*)malloc(n * n * sizeof(double));
int i, j, k;
// 存储最短路径的节点
int *pi = (int*)malloc(n * n * sizeof(int));
// 最短路径节点初始化
for (i = 0; i < n; i++) {
for (j = 0; j < n; j++) {
// 顶点到自身的路径,顶点到某个无法直接到达的顶点之间路径,初始化为-1
if (j == i || w[i * n + j] >= DBL_MAX) {
pi[i * n + j] = -1;
} else {
pi[i * n + j] = i;
}
}
}
// 内存复制,数组的拷贝(动态申请内存的数组),更简洁
memcpy(d, w, n * n * sizeof(double));
//计算最短路径,并保存顶点数据
for (k = 1; k <= n; k++) { // 以下计算,顶点k,对应于其他顶点的最短路径
for (i = 0; i < n; i++) {
for (j = 0; j < n; j++) {
// 若D[i,j]>D[i,k]+D[k,j],即经过顶点K后,路径变短,则将顶点K加入到[i,j]的路径中
if (d[i * n + j] > d[i * n + k - 1] + d[(k - 1) * n + j]) {
// 更新巨鹿数据D[i,j]
d[i * n + j] = d[i * n + k - 1] + d[(k - 1) * n + j];
// 更新顶点数据:顶点k对应的前驱节点,即当前顶点对应的一个奠定
pi[i * n + j] = pi[(k - 1) * n + j];
}
}
}
}
// 需要返回两个数组,可以使用结构体
return make_pair(d, pi);
}
路径打印:
void printAllPairsShortestPath(int *pi, int n, int i, int j)
{
// 顶点到自身的距离为0,由于初始化时将距离矩阵的对角线初始化为-1,此时将i+1即可
if (i == j) {
printf("%d ", i + 1);
return ;
}
// 若距离矩阵中的顶点不存在时,其路径也不存在
if (pi[i * n + j] == -1) {
printf("no path from %d to %d exists.
", i + 1, j + 1);
} else {
// 递归打印前驱节点
printAllPairsShortestPath(pi, n, i, pi[i * n + j]);
printf("%d ", j + 1);
}
}
三、测试结果
测试代码:
#include <stdio.h>
#include <float.h>
#include <stdlib.h>
#include <string.h>
typedef struct {
void *first;
void *second;
} pair;
pair make_pair(void *f, void *d) {
pair p = {f, d};
return p;
}
pair floydWarshall(double *w, int n)
{
// 具体实现参考上一小节
}
void printAllPairsShortestPath(int *pi, int n, int i, int j)
{
// 具体实现参考上一小节
}
int main(void)
{
// 初始化
double w[] = {0, 3, 8, DBL_MAX, -4,
DBL_MAX, 0, DBL_MAX, 1, 7,
DBL_MAX, 4, 0, DBL_MAX, DBL_MAX,
2, DBL_MAX, -5, 0, DBL_MAX,
DBL_MAX, DBL_MAX, DBL_MAX, 6, 0};
double *d;
int i, j, k, *pi;
int n = 5;
pair r;
// 计算最短路径
r = floydWarshall(w, n);
// 各顶点间的最短距离
d = (double *)r.first;
// 各顶点对应的前驱节点
pi = (int * )r.second;
printf("
---Shortest distance---
");
for (i = 0; i < n; i++) {
for (j =0; j < n; j++) {
printf("%1.1f ", d[i * n + j]); }
printf("
");
}
printf("
---Precursor node---
");
for (i = 0; i < n; i++) {
for (j =0; j < n; j++) {
printf("%2d ", pi[i * n + j]);
}
printf("
");
}
for (i = 0; i < n; i++) {
printf("
---Shortest path:[%d,x]:---
", i + 1);
for (j =0; j < n; j++) {
printAllPairsShortestPath(pi, n, i, j);
printf(":%2.1f
", d[i * n + j]);
}
}
free(d);
free(pi);
while (1);
return 0;
}
测试数据:

测试结果:
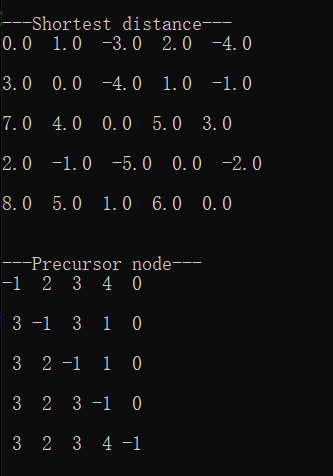
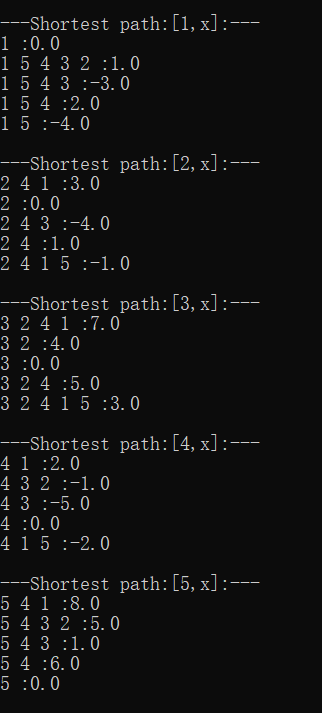
四、leetcode
待补充