刷题-力扣-108. 将有序数组转换为二叉搜索树

108. 将有序数组转换为二叉搜索树

题目链接

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/convert-sorted-array-to-binary-search-tree
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

题目描述

给你一个整数数组 nums ，其中元素已经按 升序 排列，请你将其转换为一棵 高度平衡 二叉搜索树。
高度平衡 二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不超过 1 」的二叉树。

示例 1：

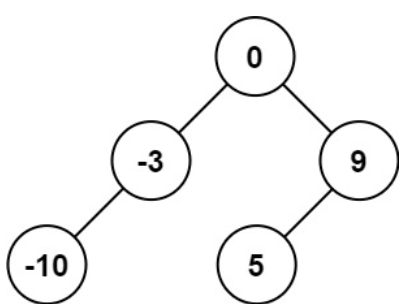
输入：nums = [-10,-3,0,5,9]
输出：[0,-3,9,-10,null,5]
解释：[0,-10,5,null,-3,null,9] 也将被视为正确答案：
![](https://img2020.cnblogs.com/blog/2151155/202108/2151155-20210806204717833-1699454210.png)

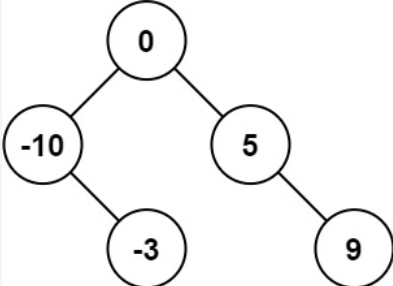
示例 2：

输入：nums = [1,3]
输出：[3,1]
解释：[1,3] 和 [3,1] 都是高度平衡二叉搜索树。

提示：

• 1 <= nums.length <= 104
• -104 <= nums[i] <= 104
• nums 按 严格递增 顺序排列

题目分析

1. 根据题目描述，将有序数组转换为排序二叉树
2. 选择数组中间的值作为根节点，数组两边的子数组分别作为左右子树
3. 根据2中的思想，使用递归的算法实现

代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* sortedArrayToBST(vector<int>& nums) {
        return recursion(nums, 0, nums.size() - 1);
    }

private:
    TreeNode* recursion(vector<int>& nums, int left, int right) {
        if (left > right) return nullptr;
        int mid = left + (right - left) / 2;
        TreeNode* root = new TreeNode(nums[mid]);
        root->left = recursion(nums, left, mid - 1);
        root->right = recursion(nums, mid + 1, right);
        return root;
    }

};