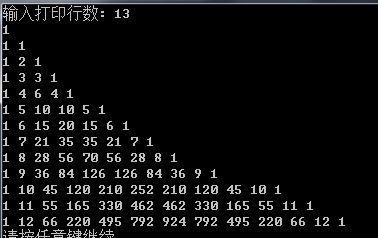
做小米的笔试题,给出一个整数n,求出它在杨辉三角形中第一次出现的行号。

想了半天,只能暴力法,从第1行开始找,一直找到第n行,若找得到则返回行号,若找不到则返回n+1(因为第n+1行第2列肯定是n)。当然,注意1是在第1行而不是第2行。更好的方法倒是没想到,倒是折腾出了打印杨辉三角形前n行的最优方法。
如果空间不限制的话,就直接定义二维数组a[n][n],初始时a[0][0]=1,通过a[i][j]=a[i-1][j]+a[i-1][j-1]计算即可。这里主要注意的就是边界条件,每一行首尾必须为1,只有夹在首尾中间的n-2个元素才适用于这个公式。
不过后来发现,只是打印的话,完全可以用2个一维数组来表示前一行和当前行。用vector表示的话就是v1和v2,每次通过v1计算出v2,打印完v2之后迭代(用v2给v1赋值)。后来发现除了vector可能重新分配的问题(这里可以vector初始化大小为n来解决),用v2给v1赋值还是很没必要的。
于是想到了可以直接交换指针,v1和v2分配足够大空间后就一直不改变大小,然后int* p1 = &v1[0]; int* p2 = &v2[0];然后每次迭代只需要std::swap(p1,p2)即可。
这里相当于就是用了2片缓冲区(固定大小),其实知道行数上限的话,用2个数组表示也一样。
最后发现,缓冲区一片就够了,这里和copy/copy_backward的原理是类似的,只要从后往前遍历的话就不会导致新元素覆盖了旧元素从而计算出错。
然后更进一步,杨辉三角形每一行是对称的。于是我们只需要取前半部分即可,对于奇数行取(n+1)/2个,对于偶数行取n/2个,按照C/C++中除法取整来看都是(n+1)/2个。
关键是,第2k+1行和第2k+2行的前半部分元素数量相同(比如第3行是1,2,第4行是1,3),而第2k+3行最后一个元素无法直接计算。其实仔细看看就会发现规律,由于对称性,第2k+3行最后一个元素是第2k+2行最后一个元素的2倍。
到这里就可以写代码了,但是写代码的时候直接按这个思路来代码会很丑,因为奇数行最后一个元素的计算方式和前面元素的计算方式不一致。一个优雅的写法是,每当从偶数行跳到奇数行时,元素数量增加,并且初始时在末尾添加一个元素,再批量计算。
比如第4行是1 3,那么第5行初始化后就是1 3 3。然后a[2] = a[1] + a[0]; a[1] = a[1] + a[0];来计算。
// 打印杨辉三角形的前n行 void printPascalTriangle(int n) { int maxrow = (n + 1) / 2; vector<int> v(maxrow + 1); v[0] = 1; // 哨兵节点 bool bOddRow = true; // 奇数行则为true int num = 0; // 需要计算的元素数量 for (int row = 1; row <= n; row++) { if (bOddRow) { num++; v[num] = v[num - 1]; } for (int i = num; i > 1; i--) v[i] += v[i - 1]; for (int i = 1; i <= num; i++) // 正向打印 cout << v[i] << " "; if (!bOddRow) // 对于偶数行最后一个元素需要再打印一遍 cout << v[num] << " "; for (int i = num - 1; i >= 1; i--) // 反向打印 cout << v[i] << " "; cout << endl; bOddRow = bOddRow ? false : true; // 行号+1后改变了奇偶性 } }