Lucas定理的基础问题

这个问题就是简单的Lucas定理的基础的问题，但是还是应该自己写一下的。

#include<bits/stdc++.h>
#define ll long long
using namespace std;
ll ans;
ll powmod(ll a, ll b,ll p)
{
    ll ans = 1;
    a %= p;
    while(b)
    {
        if(b & 1)
        {
            ans = ans * a % p;
            b--;
        }
        b >>= 1;
        a = a * a % p;
    }
    return ans;
}
ll C(ll n,ll m,ll mod)
{
    //cout<<n<<" "<<m<<endl;
    if(n==m) return 1;
    if(n<m) return 0;
    ll ans=1;
    for(int i=1;i<=m;i++)
    {
        int x=n-i+1;
        int y=m-i+1;
        ans=(ans%mod)*((x*powmod(y,mod-2,mod))%mod);
        ans%=mod;
    }
    return ans;
}
ll lucas(ll n,ll m,ll mod)
{
    if(m==0) return 1;
    return ((C(n%mod,m%mod,mod)%mod)*(lucas(n/mod,m/mod,mod)%mod))%mod;
}
int main()
{
    int t;
    scanf("%d",&t);
    while(t--)
    {
        ll n,m,p;
        ans=0;
        scanf("%lld%lld%lld",&n,&m,&p);
        cout<<lucas(n,m,p)<<endl;
    }
}

因为FZU现在不能提交所以说我也不知道对不对，但是感觉应该是对的。

DP?

Time Limit: 10000/3000 MS (Java/Others)    Memory Limit: 128000/128000 K (Java/Others)
Total Submission(s): 3137    Accepted Submission(s): 985

Problem Description

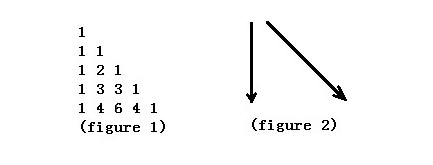
Figure 1 shows the Yang Hui Triangle. We number the row from top to bottom 0,1,2,…and the column from left to right 0,1,2,….If using C(n,k) represents the number of row n, column k. The Yang Hui Triangle has a regular pattern as follows.
C(n,0)=C(n,n)=1 (n ≥ 0)
C(n,k)=C(n-1,k-1)+C(n-1,k) (0<k<n)
Write a program that calculates the minimum sum of numbers passed on a route that starts at the top and ends at row n, column k. Each step can go either straight down or diagonally down to the right like figure 2.
As the answer may be very large, you only need to output the answer mod p which is a prime.

 

Input

Input to the problem will consists of series of up to 100000 data sets. For each data there is a line contains three integers n, k(0<=k<=n<10^9) p(p<10^4 and p is a prime) . Input is terminated by end-of-file.

 

Output

For every test case, you should output "Case #C: " first, where C indicates the case number and starts at 1.Then output the minimum sum mod p.

 

Sample Input

1 1 2 4 2 7

 

Sample Output

Case #1: 0 Case #2: 5

 

 

对于这个问题我们应该明白两点的东西就是 1、题目是dp?所以我们不能往dp的方向想，要不就完蛋，

                                                       2、 我们应该知道的是最小的路径肯定是经过的1最多，然后就是我们画个图然后推道一下。

知道了这两点我们就可以退出来一个公式，c(n+1,k)+n-k.

然后我们用Lucas定理来解决就行了 ，但是还是应该注意一个问题就是我们应该预处理阶乘，这样子的话就不会时间超限了，因为这个T的范围真的是大.

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=1e4+4;
int vis[N],prime[N];
ll fac[N][N],inv[N][N];
int cnt=0;
void get()
{
    for(int i=2;i<=10000;i++)
    {
        if(!vis[i])
        {
            prime[++cnt]=i;
            for(int j=i*2;j<=10000;j+=i)
            {
                vis[j]=1;
            }
        }
    }
}
ll powmod(ll a, ll b,ll p)
{
    ll ans = 1;
    a %= p;
    while(b)
    {
        if(b & 1)
        {
            ans = ans * a % p;
            b--;
        }
        b >>= 1;
        a = a * a % p;
    }
    return ans;
}
void inist()
{
    for(int i=1;i<=cnt;i++)
    {
        fac[prime[i]][0]=inv[prime[i]][0]=1;
        fac[prime[i]][1]=inv[prime[i]][1]=1;
        for(int j=2;j<prime[i];j++)
        {
            fac[prime[i]][j]=(fac[prime[i]][j-1]*j)%prime[i];
            inv[prime[i]][j]=(inv[prime[i]][j-1]*powmod(j,prime[i]-2,prime[i]))%prime[i];
        }
    }
}
ll C(int n,int m,int mod)
{
    if(n<m) return 0;
    if(n==m) return 1;
    ll x=fac[mod][n];
    ll y=inv[mod][m]*inv[mod][n-m];
    y=y%mod;
    return ((x%mod)*(y%mod))%mod;
}
ll Lucas(int n,int m,int mod)
{
    if(m==0)return 1;
    return (C(n%mod,m%mod,mod)*Lucas(n/mod,m/mod,mod))%mod;
}
int main()
{
    get();
    inist();
    int n,m,mod;
    int id=0;
    while(~scanf("%d%d%d",&n,&m,&mod))
    {
        if (2*m > n)
            m = n-m;
        n++;
        id++;
        printf("Case #%d: ",id);
        printf("%lld
",(Lucas(n,m,mod)+n-m-1)%mod);
    }
}