2020牛客暑期多校训练营(第六场) J. Josephus Transform

• 题意

  • 给你一个长度为 (n) 的排列 (P) (初始化为 (P = {1,2,...,n})) 和 (m) 次操作，每次操作是一对((k,x))表示对排列(P) 进行 (x) 次 (K- Josephus transform)。

• 解析

  • 发现对 (P) 进行一次 (K- Josephus transform)，实际上就是对 (P) 进行一次置换，设这个置换为 (T) ,进行(x) 次就是对 (P) 进行 (x) 次置换 (T) 。如果我们能得到置换 (T) ，那么进行 (x) 次就可以用快速幂 (nlogx) 实现。
  • 现在我们要考虑如何得到置换 (T) ，得到置换 (T) 实际上就是要知道对排列 (P) 进行一次 (K- Josephus transform) 后的排列 (P')
  • 令 (vis[i] = 1) 表示 (i) 没有被取出，(Sum[i]) 为 (vis[i]) 的前缀和 。
  • 令上一次被取出的数是第 (pos) 个，当前还剩下 (cnt) 个数字，那么下一个被取出来的数是剩下的第 ((pos-1+k -1)\%cnt + 1)
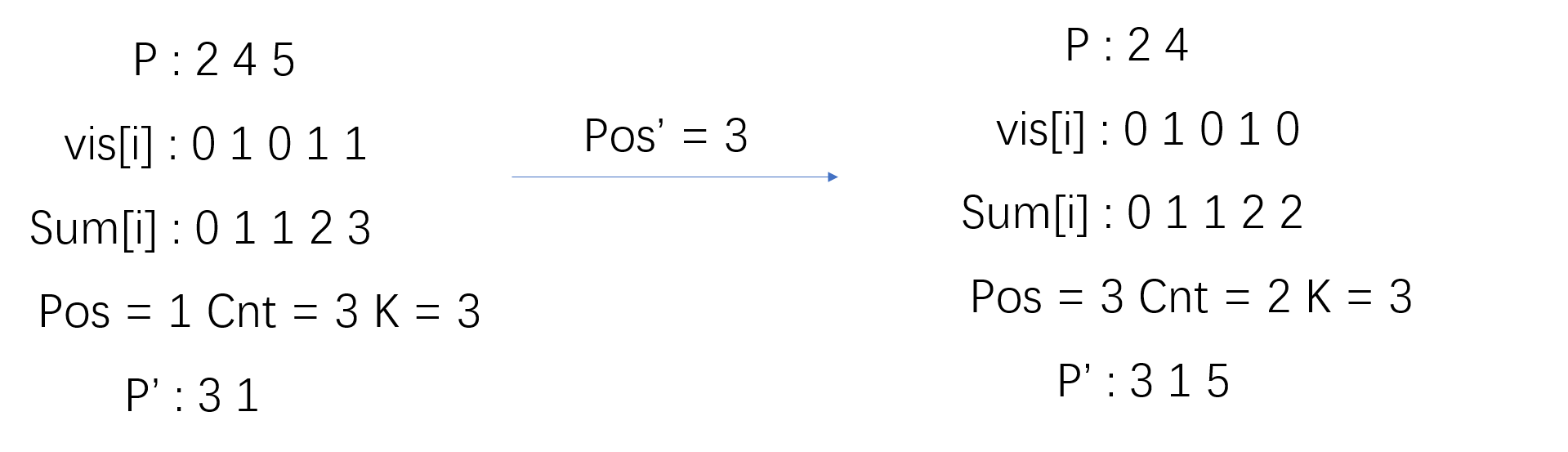
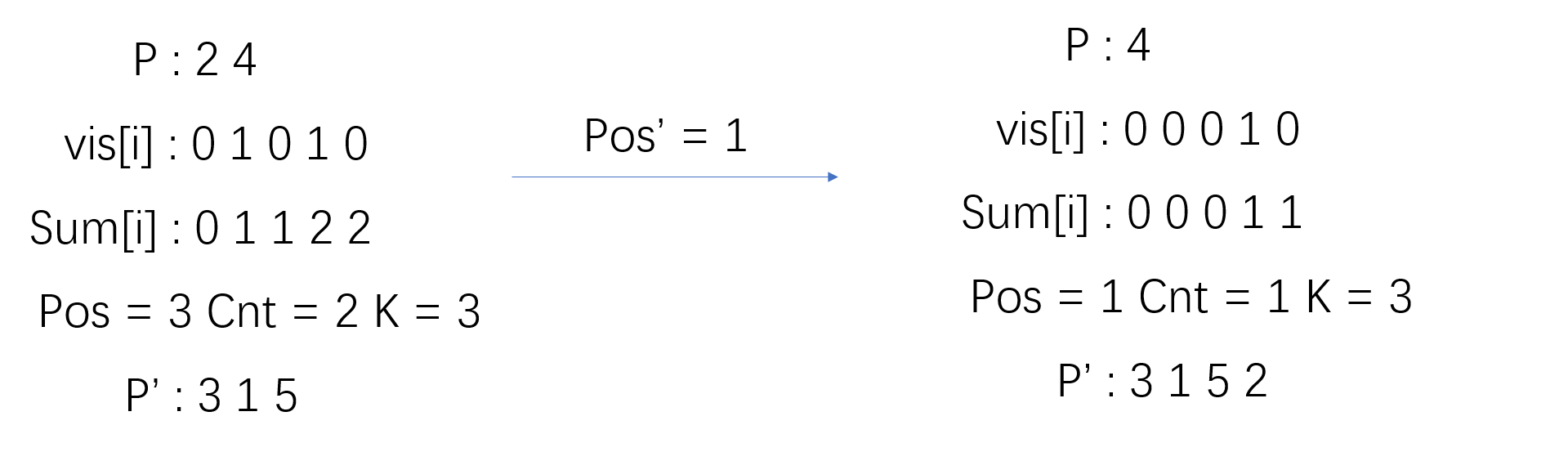
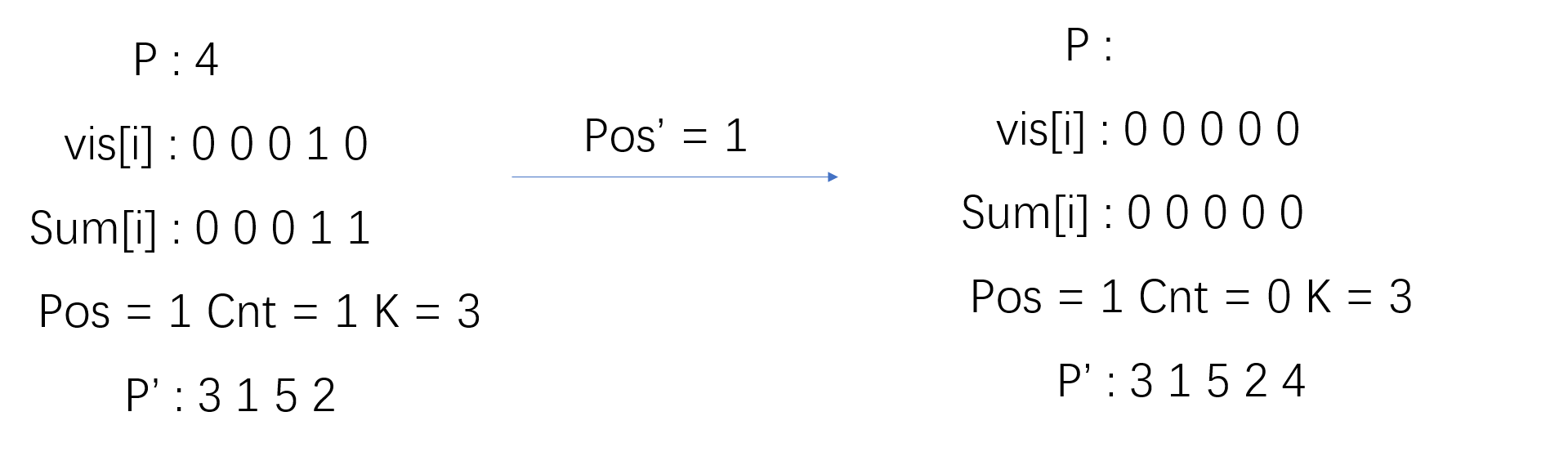
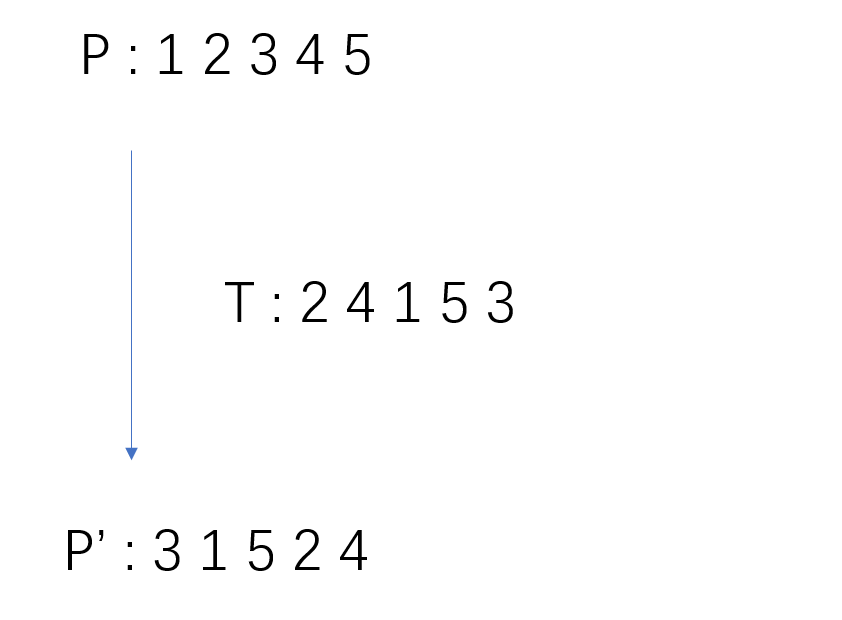
  • 对于 (n = 5,k = 3) 的一次变化如下图
  • 
  

  • 对排列 ({1,2,3,4,5}) 进行一次 (3- Josephus transform) 发现每次的 (pos') 实际上就是原数组 (Sum[i] = pos') 的第一个位置( 被取出的数的就是 (i) ，因为排列是 ({1,2,3,4,5}) ，第 (i) 位置上的数就是本身)

  • 如果用上述前缀和的形式来得到 (P') 复杂度就是 (n^2)

  • 如果考虑用树状数组优化，采用二分判断当前位置的前缀和是否为 (pos') ( 记得是找第一个位置 )，因为树状数组求前缀的复杂度为 (logn) 所以整体复杂度就是 (nlognlogn) ~~~( 不知道会不会超时 ) ~~~

  • 由于树状数组求一段区间的和是 (logn) ,我们还可以考虑用线段树来维护v

  • 若你现在需要找到区间 ([L,R]) 前缀和为 (v) 的第一个位置，如果左子树的 (Sum) 比 (v) 大，那么你要找的就在左子树上，否则你就要找右子树中 (v-Sum) 的那个位置

  • int Query(int t,int v){
        if( l(t) == r(t) )  return l(t);
        if( s(L) >= v )  return Query(L,v);
        else return Query(R,v-s(L));
    }
    

  • 再来考虑一下最后一步快速幂怎么写

  • 我们知道一次置换是 (T) ，跟快速幂一样，(T^2,T^4...) 都只需要平方一下，那么如果 (x) 在二进制下第(i)位置上为 (1) ，再用对 (P) 进行一次 (T^{1<<i}) 的置换

• 代码

  • #include <bits/stdc++.h>
    
    #define L t<<1
    #define R L|1
    #define l(a) ST[a].l
    #define r(a) ST[a].r
    #define s(a) ST[a].sum
    
    using namespace std;
    typedef long long ll;
    typedef pair<int,int> pii;
    const int Maxn = 1e6+10;
    const int Inf = 0x7f7f7f7f;
    const int Mod = 1e9+7;
    const double eps = 1e-7;
    
    struct Segment_Tree{
        int l,r,sum;
    }ST[Maxn << 2];
    
    void Updata(int t){
        s(t) = s(L) + s(R);
    }
    void Build(int t,int ll,int rr){
        l(t) = ll, r(t) = rr;
        if( ll == rr )
        {
            s(t) = 1;
            return ;
        }
        int mid = (ll + rr) >> 1;
        Build(L,ll,mid);
        Build(R,mid+1,rr);
        Updata(t);
    }
    void Change(int t,int pos,int v){
        if( pos < l(t) || r(t) < pos )  return ;
        if( l(t) == pos && r(t) == pos )
        {
            s(t) = v;
            return ;
        }
        Change(L,pos,v);
        Change(R,pos,v);
        Updata(t);
    }
    int Query(int t,int v){
        if( l(t) == r(t) )  return l(t);
        if( s(L) >= v )  return Query(L,v);
        else return Query(R,v-s(L));
    }
    
    int ch[Maxn],per[Maxn],tmp[Maxn];
    void _2(int n){
        for(int i=1;i<=n;i++)   tmp[i] = ch[ ch[i] ];
        for(int i=1;i<=n;i++)   ch[i] = tmp[i];
    }
    void change(int n){
        for(int i=1;i<=n;i++)   tmp[ch[i]] = per[i];
        for(int i=1;i<=n;i++)   per[i] = tmp[i];
    }
    
    int main(){
        int n,m;
        scanf("%d %d",&n,&m);
        for(int i=1;i<=n;i++)  per[i] = i;
        for(int i=1,k,x;i<=m;i++)
        {
            scanf("%d %d",&k,&x);
            Build(1,1,n);
            int pos = 1, cnt = n;
            for(int i=1;i<=n;i++)
            {
                int Now_pos = (pos-1+k-1)%cnt + 1;
                pos = Now_pos, cnt--;
                Now_pos = Query(1,Now_pos);
                Change(1,Now_pos,0);
                tmp[i] = Now_pos, ch[i] = i;
            }
            for(int i=1;i<=n;i++)  ch[tmp[i]] = i;
            while( x )
            {
                if( x&1 )  change(n);
                _2(n);
                x >>= 1;
            }
        }
        for(int i=1;i<=n;i++)  printf("%d ",per[i]);
        return 0;
    }