拉格朗日对偶问题的直观理解

拉格朗日对偶问题的理解

拉格朗日乘数法

拉格朗日乘数法本身就是帮助我们求函数的最值。在数学最优问题中，拉格朗日乘数法（以数学家约瑟夫·路易斯·拉格朗日命名）是一种寻找变量受一个或多个条件所限制的多元函数的极值的方法。

对于一个函数，我们要求其最值，只要对该函数求导得到所有极值点，然后根据要求的是最大值或最小值，从所有极值点中选择最大或最小即可。

但是如果是有约束条件的函数，极值点可能不在约束的条件范围内，也就是说，在约束范围内，函数没有导数为\(0\)的点。因此，拉个朗日乘数法就是解决该问题的。它告诉我们只需要对原来函数和约束条件变形，写到一个式子中，后只要对该式子进行求极值，求最值就可以得到最终要的结果了。

\[\begin{align} min\;&f_0(\boldsymbol{x}),\boldsymbol{x}\in R^n\\ s.t.\; &f_i(\boldsymbol{x})\le0,\text{其中}i=1,2,3,\dots, m \end{align} \]

拉个朗日乘数法也就是可以将上述问题转换为一下问题求解：

\[\begin{align} L(\boldsymbol{x},\boldsymbol{\lambda})=f_0(\boldsymbol{x})+\sum\lambda_if_i(\boldsymbol{x}) \end{align} \]

其中，\(f_0(\boldsymbol{x})\)叫做目标函数，\(s.t. f_i(\boldsymbol{x})\le0\)，叫做约束条件。\(\boldsymbol{x}\)的取值范围叫做可行域。\(L(\boldsymbol{x},\boldsymbol{\lambda})\)叫做拉格朗日函数。

拉格朗日乘数法的直观理解

对于目标函数\(f(\boldsymbol{x},\boldsymbol{y})\)，求其在约束条件\(\boldsymbol{y}=g(\boldsymbol{x})\)下的最小值。根据拉格朗日乘数法可以得到：

\[\begin{align} L(\boldsymbol{x},\boldsymbol{y},\lambda )=f(\boldsymbol{x},\boldsymbol{y})+\lambda(\boldsymbol{y}-g(\boldsymbol{x})) \end{align} \]

求\(\nabla L(\boldsymbol{x},\boldsymbol{y},\lambda)=0\)得：

\[\begin{align}\left\{\begin{matrix} \frac{\partial f(\boldsymbol{x},\boldsymbol{y})}{\partial \boldsymbol{x}} +\lambda \frac{\partial(\boldsymbol{y}-g(\boldsymbol{x}))}{\partial \boldsymbol{x}}=0\\ \frac{\partial f(\boldsymbol{x},\boldsymbol{y})}{\partial \boldsymbol{y}} +\lambda \frac{\partial(\boldsymbol{y}-g(\boldsymbol{x}))}{\partial \boldsymbol{y}}=0\\ \end{matrix}\right. \end{align} \]

我们结合图像来直观理解，假设目标函数\(f(\boldsymbol{x},\boldsymbol{y})\)的梯度的等高线是下图中的蓝线，约束条件\(\boldsymbol{y}=g(\boldsymbol{x})\)的梯度图像为下图中的橙线。从图像上看，要\(\nabla L(\boldsymbol{x},\boldsymbol{y})=0\)，就需要两条线相切，此时可以通过调整\(\lambda\)参数来使得两者相加的梯度等于\(0\)。

再结合式(5)，先将某一点的梯度方向分解为\(x\)轴方向和\(y\)轴方向，\(\frac{\partial f(\boldsymbol{x},\boldsymbol{y})}{\partial \boldsymbol{x}} +\lambda \frac{\partial(\boldsymbol{y}-g(\boldsymbol{x}))}{\partial \boldsymbol{x}}=0\)，相当于将\(x\)轴方向的梯度调整到\(0\)。\(\frac{\partial f(\boldsymbol{x},\boldsymbol{y})}{\partial \boldsymbol{y}} +\lambda \frac{\partial(\boldsymbol{y}-g(\boldsymbol{x}))}{\partial \boldsymbol{y}}=0\)相当于将\(y\)轴方向的梯度调整到\(0\)，因为两个方向的公用一个参数\(\lambda\)，无法改变约束条件梯度的方向，只能改变其大小。所以只有当目标函数梯度方向和约束条件的梯度方向在相同或相反方向时，才能使得两者梯度和为\(0\)。

上述只有一个约束条件，当有多个约束条件时：

\[\begin{align} min\; &f(\boldsymbol{x}), \boldsymbol{x}\in R^n\\ s.t.\; &g_i(\boldsymbol{x})=\boldsymbol{a_i}^T\cdot \boldsymbol{x}+b_i \le0 \text{其中}i=1,2,3,\dots,m,\; \boldsymbol{a_i}\in R^n, b_i \in R \end{align} \]

由拉格朗日乘数法得：

\[\begin{align} &L(\boldsymbol{x},\boldsymbol{\lambda})=f(\boldsymbol{x})+\sum_{i=1}^m\lambda_i g_i(\boldsymbol{x})\\ \end{align} \]

求\(\nabla L(\boldsymbol{x},\boldsymbol{\lambda})=0\)得：

\[\begin{align} \frac{\partial f(\boldsymbol{x})}{\partial x} +\sum_{i=1}^m \lambda_i \boldsymbol{a_i^T} =0\\ \frac{\partial f(\boldsymbol{x})}{\partial x}=-\sum_{i=1}^m \lambda_i \boldsymbol{a_i^T} \end{align} \]

假设\(n=2, m=5\)，可得到其对应大概图像为：

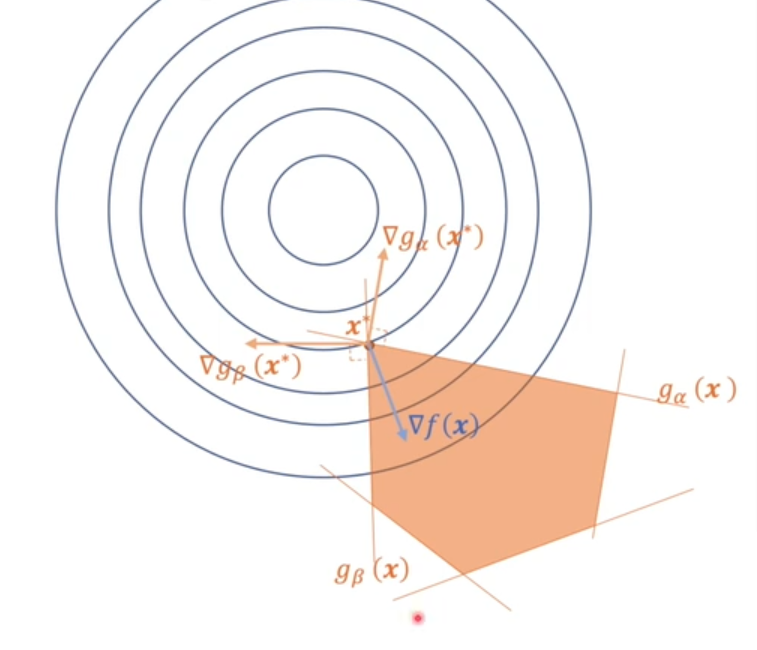
其中阴影部分为约束条件所围成的部分。可以看到，最值在\(x^*\)的位置，而约束条件中有作用的只有两个，即\(g_\alpha(\boldsymbol{x})\)和\(g_\beta(\boldsymbol{x})\)。其他三个约束条件都没有起作用。也就是说：

\[\begin{align} g_\alpha(\boldsymbol{x*})=g_\beta(\boldsymbol{x*})=0&& \text{其他}g_i(\boldsymbol{x*})<0\\ \lambda_\alpha \nabla g_\alpha(\boldsymbol{x*})+\lambda_\beta \nabla g_\beta(\boldsymbol{x*})=-\nabla f(\boldsymbol{x}) \Rightarrow \lambda_\alpha,\lambda_\beta\ne 0&& \lambda_i\cdot \nabla g_i(x)=0 \Rightarrow \lambda_i=0(i\ne \alpha, \beta) \end{align} \]

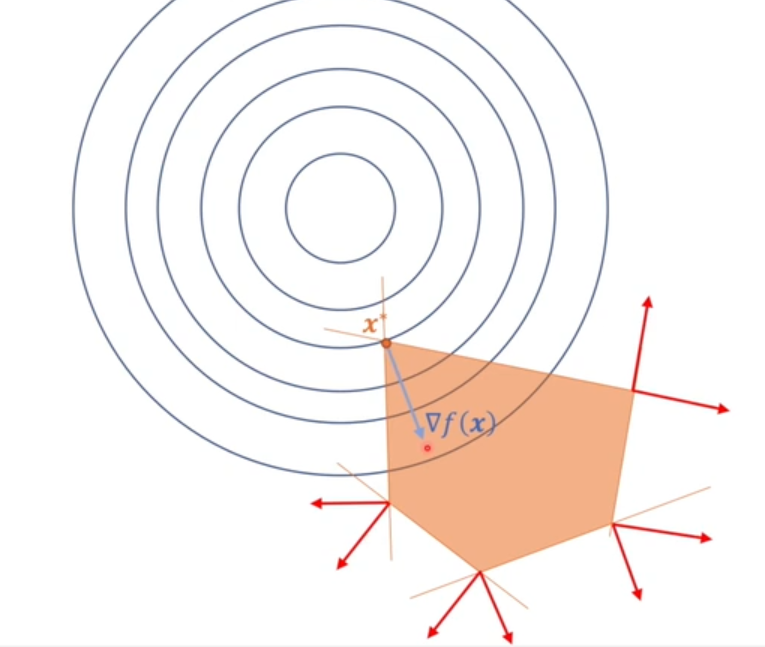
从图像上看，就是除了\(g_\alpha(\boldsymbol x)\)和\(g_\beta(x)\)的梯度合成方向可以与\(f(\boldsymbol x^*)\)的梯度方向相反，其他约束条件的梯度所合成的方向，都无法做到。因此就需要使得其\(\lambda_i=0\)。这里有一个前提条件，即\(\forall \lambda_i\ge 0\)。且

\[\begin{align} \left\{ \begin{matrix} \lambda_i =0 &\text{那么对应的约束条件}g_i(x)\text{是松弛的}\\ \lambda_i >0 &\text{那么对应的约束条件}g_i(x)\text{是紧致的} \end{matrix} \right. \end{align} \]

当最值在所有约束条件所圈定的可行域范围内时，所有的约束条件都是松弛的。

拉格朗日乘数法的存在的问题

拉格朗日乘数法找出来的可能是极值点和鞍点，即当约束条件和目标函数有多个切点时，就会有多个解。

因此对于凸优化问题，其极值就等于最值，这时就可以直接使用拉格朗日乘数法来求解。

凸集与非凸集

若集合\(C\)满足：

\[\begin{align} \forall \boldsymbol{x_1, x_2} \in C, 0\le \theta\le 1\Rightarrow \theta\cdot \boldsymbol{x_1} + (1-\theta) \cdot x_2 \in C \end{align} \]

则集合\(C\)是凸集。从图像上看如下（左边为非凸集，右边为凸集）：

仿射集一定是凸集，仿射集定义为\(C=\{x|W^T\cdot \boldsymbol x + b=0\}\)。其中\(\boldsymbol{x} \in R^n, W\in R^n, b\in R\)。且仿射集的交也是凸集。

半空间也是凸集，半空见的定义为\(C=\{x|W^T\cdot \boldsymbol x + b\le0\}\)。其中\(\boldsymbol{x} \in R^n, W\in R^n, b\in R\)。且半空间的交也是凸集。

凸函数和凹函数

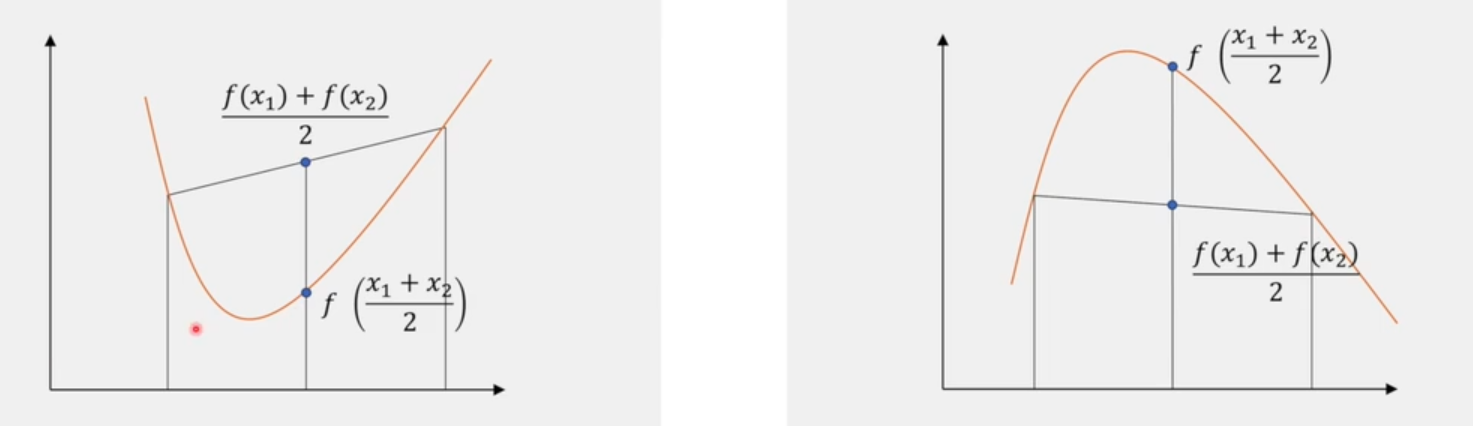
若函数\(f(x)\)满足：\(f(\frac{x_1+x_2}{2})\le \frac{f(x_1)+f(x_2)}{2}\)，则称该函数为凸函数。同理若函数\(f(x)\)满足：\(f(\frac{x_1+x_2}{2})\ge \frac{f(x_1)+f(x_2)}{2}\)，则称该函数为凹函数。(左图为凸函数，右图为凹函数)

凸优化问题

对于一个函数\(f(x)\)，若该函数是一个凸函数，且可行域是一个凸集，那么该问题就是一个凸优化问题。

拉格朗日对偶问题

对于非凸优化问题，我们可以用拉格朗日对偶问题来求解。

\[\begin{align} \text{原问题：}min\; &f_0(\boldsymbol{x}),\boldsymbol{x}\in R^n\\ s.t.\;&f_i(\boldsymbol{x})\le 0, \text{其中}i=1,2,3,\dots,m\\ &h_i(\boldsymbol{x})=0,\text{其中}i=1,2,3,\dots,q \end{align} \]

由拉格朗日乘数法得：

\[\begin{align} L(\boldsymbol{x,\lambda, \nu})=f_0(\boldsymbol x)+\sum \lambda_i f_i(\boldsymbol x) + \sum \nu_i h_i(\boldsymbol{x}) \end{align} \]

其又可转化为以下形式：

\[\begin{align} \text{原问题：}&min_{\boldsymbol{x}}max_{\boldsymbol{\lambda, \nu}} L(\boldsymbol{x, \lambda, \nu})\\ s.t.\; &\boldsymbol{\lambda}\ge \boldsymbol{0} \end{align} \]

即先将\(\boldsymbol{x}\)当作常数，把\(\boldsymbol{\lambda, \nu}\)当作变量，去求拉格朗日函数的最大值。然后在把\(\boldsymbol{x}\)当作变量从中找最小值。

证明：

从式(14),(15),(16)转换为式(18)后，\(\boldsymbol{x}\)的可行域变为了任意值。再对\(\boldsymbol{x}\)分情况讨论：

当\(\boldsymbol{x}\)不在式(14),(15),(16)的可行域内时：

\[\begin{align} max_{\boldsymbol{\lambda,\nu}}L(\boldsymbol{x,\lambda, \nu}) =f_0(\boldsymbol x)+\color{blue}{\sum \lambda_i f_i(\boldsymbol x)} + \color{red}{\sum \nu_i h_i(\boldsymbol{x})} \color{black}{=f_0(\boldsymbol x)}+\color{blue}{\infin}+\color{red}{\infin}\color{black}{=\infin} \end{align} \]

其中蓝色项中，由于\(\boldsymbol x\)不在式(14)的可行域内，即\(\lambda\ge 0,f_i(\boldsymbol x)>0\)。同理对于红色项\(h_i(\boldsymbol x)\ne 0\)。因此两项的最大值都是无穷大。

当\(\boldsymbol{x}\)在式(14),(15),(16)的可行域内时：

\[\begin{align} max_{\boldsymbol{\lambda,\nu}}L(\boldsymbol{x,\lambda, \nu}) =f_0(\boldsymbol x)+\color{blue}{\sum \lambda_i f_i(\boldsymbol x)} + \color{red}{\sum \nu_i h_i(\boldsymbol{x})} \color{black}{=f_0(\boldsymbol x)}+\color{blue}{0}+\color{red}{0}\color{black}{=f_0(\boldsymbol x)} \end{align} \]

其中蓝色项中，由于\(\boldsymbol x\)在式(14)的可行域内，即\(\lambda\ge 0,f_i(\boldsymbol x)\le 0\)。同理对于红色项\(h_i(\boldsymbol x)= 0\)。因此两项的最大值都是0。

而\(min_{\boldsymbol{x}}max_{\boldsymbol{\lambda, \nu}} L(\boldsymbol{x, \lambda, \nu})=min_x(\infin, f_0(\boldsymbol x))=min_x f_0(\boldsymbol x)\)。即\(\boldsymbol x\)在可行域内时\(f_0(\boldsymbol x)\)的最小值。

对偶问题

式(18)又可表示为：

\[\begin{align} \text{对偶问题：}&max_{\boldsymbol{\lambda, \nu}} min_{\boldsymbol{x}}L(\boldsymbol{x,\lambda, \nu})\\ s.t.\; &\boldsymbol{\lambda \ge 0} \end{align} \]

即先将\(\boldsymbol{\lambda, \nu}\)当作常数，把\(\boldsymbol{x}\)当作变量去求拉格朗日函数的最小值，再把\(\boldsymbol{\lambda, \nu}\)当作变量，去求最大值。

对偶问题的一个特性就是，无论原问题是什么，只要换成对偶问题，它都是一个凸优化问题。

证明

假设我们找到当\(\boldsymbol{x=x^*}\)时，此时\(min_{\boldsymbol{x}}L(\boldsymbol{x,\lambda, \nu})=L(\boldsymbol{x^*, \lambda, \nu})\)。所以：

\[\begin{align} max_{\boldsymbol{\lambda, \nu}} min_{\boldsymbol{x}}L(\boldsymbol{x,\lambda, \nu}) =max_{\boldsymbol{\lambda, \nu}}\color{gray}{f_0(x^*)}\color{black}{+\sum \lambda_i} \color{gray}{f_i(x^*)}\color{black} {+\sum \nu_i}\color{gray}{h_i(x^*)} \end{align} \]

其中灰色部分都是常数，因此整个\(\color{gray}{f_0(x^*)}\color{black}{+\sum \lambda_i} \color{gray}{f_i(x^*)}\color{black} {+\sum \nu_i}\color{gray}{h_i(x^*)}\)为关于参数\(\boldsymbol{\lambda, \nu}\)的一条直线。也就是说它即是凸函数，又是凹函数。在约束条件中，要求\(\boldsymbol{\lambda}\ge 0\)，即可行域是一个半空间，前面说过半空间一定是凸集。因此对偶问题一定是凸优化问题。

原问题的解与对偶问题的解的关系

对于以下原问题和对偶问题：

\[\begin{align} \text{原问题：}&min_{\boldsymbol{x}}max_{\boldsymbol{\lambda, \nu}} L(\boldsymbol{x, \lambda, \nu})\\ s.t.\; &\boldsymbol{\lambda}\ge \boldsymbol{0} \end{align} \]

\[\begin{align} \text{对偶问题：}&max_{\boldsymbol{\lambda, \nu}} min_{\boldsymbol{x}}L(\boldsymbol{x,\lambda, \nu})\\ s.t.\; &\boldsymbol{\lambda \ge 0} \end{align} \]

可以容易得到：

\[\begin{align} max_{\boldsymbol{\lambda, \nu}}L(\boldsymbol{x, \lambda, \nu})\ge L(\boldsymbol{x, \lambda, \nu})\ge min_xL(\boldsymbol{x, \lambda, \nu}) \end{align} \]

也就是说无论\(\boldsymbol{x,\lambda, \nu}\)取何值，以下不等式恒成立：

\[\begin{align} A(\boldsymbol{x})=max_{\boldsymbol{\lambda, \nu}}L(\boldsymbol{x, \lambda, \nu})\ge min_xL(\boldsymbol{x, \lambda, \nu})=I(\boldsymbol{\lambda, \nu}) \end{align} \]

因此：

\[\begin{align} min_{\boldsymbol{x}}\; A(\boldsymbol{x}) \ge max_{\boldsymbol{\lambda, \nu}}\; I(\boldsymbol{\lambda, \nu}) \end{align} \]

即原问题的解大于等于对偶问题的解。

解的关系的直观理解

对于以下原问题和对偶问题：

\[\begin{align} \text{原问题：}min\; &f_0(\boldsymbol{x}),\boldsymbol{x}\in R^n\\ s.t.\;&f_i(\boldsymbol{x})\le 0, \text{其中}i=1,2,3,\dots,m\\ &h_i(\boldsymbol{x})=0,\text{其中}i=1,2,3,\dots,q \end{align} \]

\[\begin{align} \text{对偶问题：}&max_{\boldsymbol{\lambda, \nu}} min_{\boldsymbol{x}}L(\boldsymbol{x,\lambda, \nu})\\ s.t.\; &\boldsymbol{\lambda \ge 0} \end{align} \]

其中:

\[\begin{align} L(\boldsymbol{x,\lambda, \nu})=f_0(\boldsymbol x)+\sum \lambda_i f_i(\boldsymbol x) + \color{gray}{\sum \nu_i h_i(\boldsymbol{x})} \end{align} \]

其中因为\(h_i(\boldsymbol{x})=0\)，所以灰色部分等于\(0\)，可以不考虑。将上式简化为矩阵表示：

\[\begin{align} L(\boldsymbol{x, \lambda, \nu})=t+\boldsymbol{\lambda^T\cdot u} \end{align} \]

式(39)在原问题中的可行域为：

\[\begin{align} G_1=\{(t, \boldsymbol{u})|t=f_0(\boldsymbol{x}), u_i=f_i(\boldsymbol{x}), \color{red}{\boldsymbol{x} \in D}\color{black}{\}}\\ D=\left\{x\left| \begin{matrix} f_i(\boldsymbol{x})\le0, \text{其中}i=1,2,3,\dots,m\\ h_i(\boldsymbol{x})=0,\text{其中}i=1,2,3,\dots,q \end{matrix} \right.\right\} \end{align} \]

因此原问题又可描述为：

\[\begin{align} min_{\boldsymbol{x}} \{t|(t,\boldsymbol{u})\in G_1, \color{gray}{\boldsymbol{u\le 0}}\color{black}{\}} \end{align} \]

式(39)在对偶问题中的可行域为：

\[\begin{align} G_2=\{(t, \boldsymbol{u})|t=f_0(\boldsymbol{x}), u_i=f_i(\boldsymbol{x}), \color{red}{\boldsymbol{x} \in R^n}\color{black}{\}}\\ \end{align} \]

因此对偶问题又可描述为：

\[\begin{align} max_{\boldsymbol{\lambda}}min_{\boldsymbol{x}}\{t+\boldsymbol{\lambda^T}\cdot \boldsymbol{u}| (t,\boldsymbol{u}\in G_2, \color{red}{ \lambda\ge 0 }\color{black}{\}} \end{align} \]

用图像来表示上述两个问题：

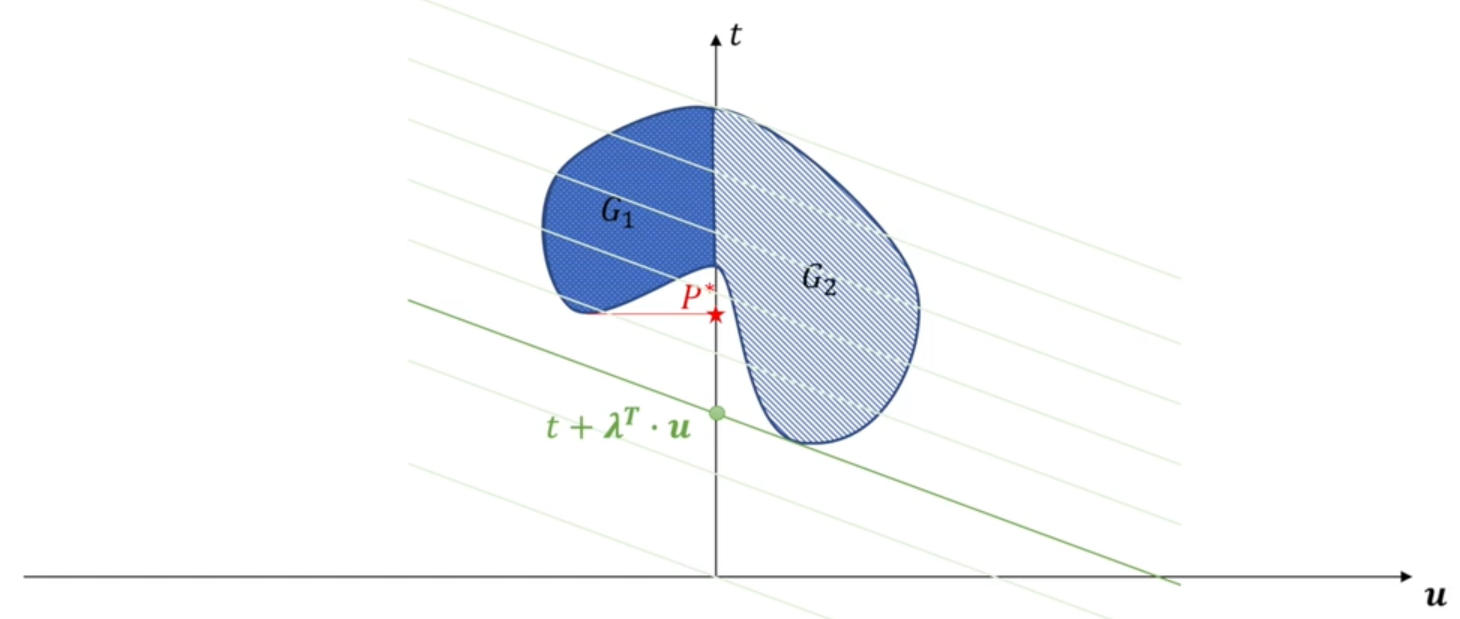
对于上图，\(G_2\)为整个实线所围成的整个区域，而\(G_1\)仅为\(t\)轴的左半边部分。因此\(P^*\)在\(t\)轴上的位置，表示为原问题的解的大小。

对于对偶问题，第一步先将\(\lambda\)看作常数，即直线的斜率不变，然后上下平移选择一条直线，该直线的截距最小，且与\(G_2\)相交（也就是上图绿色的线）。

由于：

\[\begin{align} ax+by=c\\ \frac{a}{b}x+y=\frac{c}{a} \end{align} \]

\(\frac{c}{a}=y+\frac{a}{b}x\)就是直线的截距，因此\(t+\boldsymbol{\lambda^T\cdot u}\)就是函数的截距。

第二步在保证相切的情况下，改变斜率的大小，使得截距最大。因此对偶问题的最优解为\(D^*\)，如上图所示。

可以看出，原问题的解是大于等于对偶问题的解的。此时我们把原问题和对偶问题叫做弱对偶。只有当\(P^*\)和\(D^*\)相等的时候，才称原问题和对偶问题为强对偶，此时可行域的范围是一个凸集。

Slater条件

一个问题是凸优化问题，它不一定是强对偶关系，只有这个凸优化问题满足Slater条件时，该问题才是强对偶的。

对于一个凸优化问题：

\[\begin{align} \text{原问题：}min\; &f_0(\boldsymbol{x}),\boldsymbol{x}\in R^n\\ s.t.\;&f_i(\boldsymbol{x})\le 0, \text{其中}i=1,2,3,\dots,m\\ &h_i(\boldsymbol{x})=0,\text{其中}i=1,2,3,\dots,q \end{align} \]

当其满足以下条件(Slater条件)：

\[\begin{align} &\text{存在一个点} x\in relint\; D\\ &\text{使得}f_i(x)<0,\text{其中}i=1,2,3...m,A\boldsymbol{x}=b\\ &(relint\;D\text{表示可行域}D\text{的相对内部，也就是不能在边界上}) \end{align} \]

则该凸优化问题时强对偶的。

注：强对偶的不一定满足Slater条件

KKT条件

只有某个问题是强对偶的，那么它一定满足KKT条件。同样反过来就不一定。

对于一个凸优化问题：

\[\begin{align} \text{原问题：}min\; &f_0(\boldsymbol{x}),\boldsymbol{x}\in R^n\\ s.t.\;&f_i(\boldsymbol{x})\le 0, \text{其中}i=1,2,3,\dots,m\\ &h_i(\boldsymbol{x})=0,\text{其中}i=1,2,3,\dots,q\\ \end{align} \]

由拉格朗日乘数法得：

\[\begin{align} L(\boldsymbol{x,\lambda, \nu})=f_0(\boldsymbol x)+\sum \lambda_i f_i(\boldsymbol x) + \sum \nu_i h_i(\boldsymbol{x}) \end{align} \]

当其是强对偶问题时，它一定满足以下条件(KKT条件)：

\[\begin{align} \left.\begin{matrix} f_i(x)\le0\\ h_i(x)=0\\ \end{matrix}\right\} \text{ 原问题可行条件}\\\\ \left.\begin{matrix} \nabla_xL(\boldsymbol{x,\lambda,\nu})=0\\ \lambda\ge0\\ \end{matrix}\right\} \text{ 对偶问题可行条件}\\\\ \left.\begin{matrix} \lambda_if_i(\boldsymbol{x})=0 \end{matrix}\right\} \text{ 互补松弛条件}\\ \end{align} \]

前两种条件，分别是原问题和对偶问题成立的可行条件，最后一个互补松弛条件是为了同时满足小节拉格朗日乘数法的直观理解中式\(13\)，以此同时表示紧致情况和松弛情况。

推荐详细讲解视频：https://www.bilibili.com/video/BV1HP4y1Y79e