该系列为DR_CAN动态系统的建模与分析系列视频笔记,详见https://space.bilibili.com/230105574
由于笔者水平有限,文中难免存在一些不足和错误之处,诚请各位批评指正。
1 频率响应
回顾一下频率响应的结论,即振幅响应的值为 (G(jomega)) 的幅值,幅角响应的值为 (G(jomega)) 的幅角:
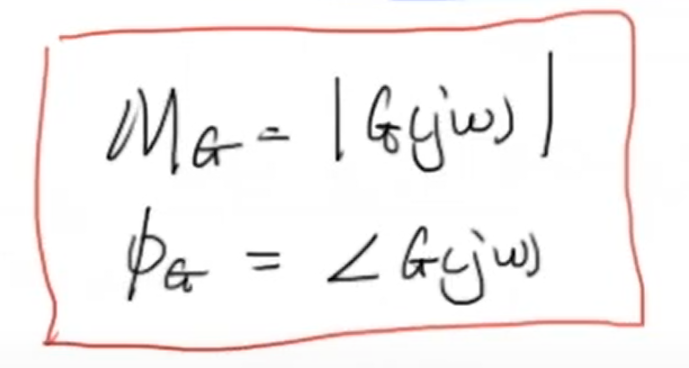
2 二阶系统
回顾二阶系统基本形式,我们有以下内容,其中 (u(t) = frac{F}{omega^2}) 旨在单位化,都是以前的内容这里不再赘述:
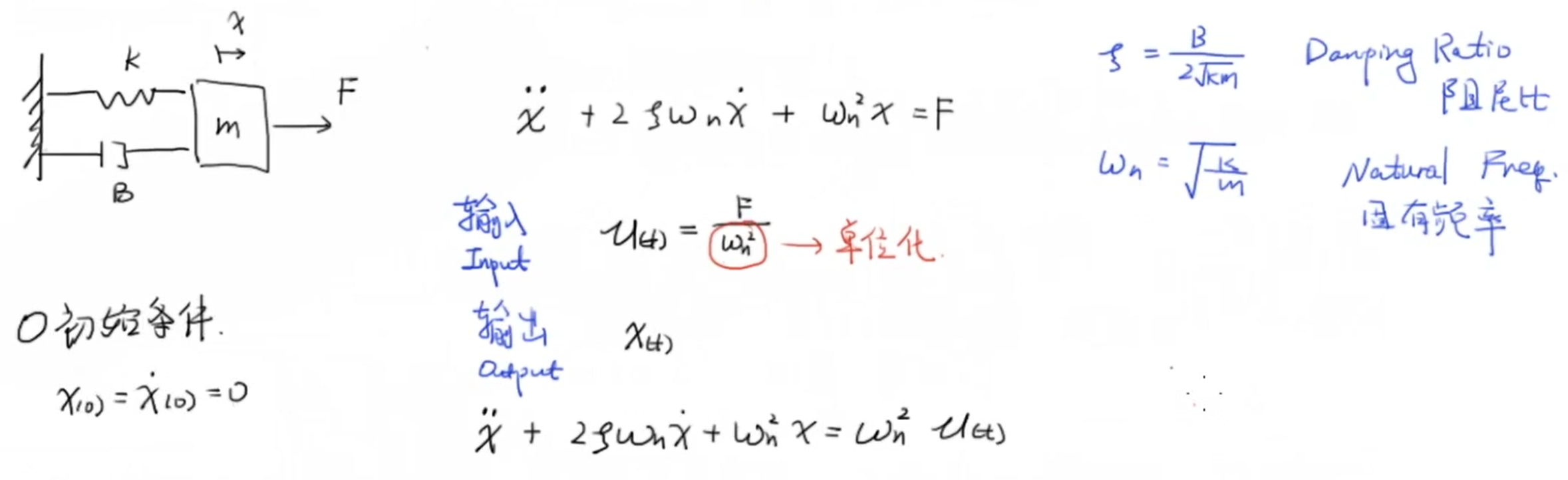
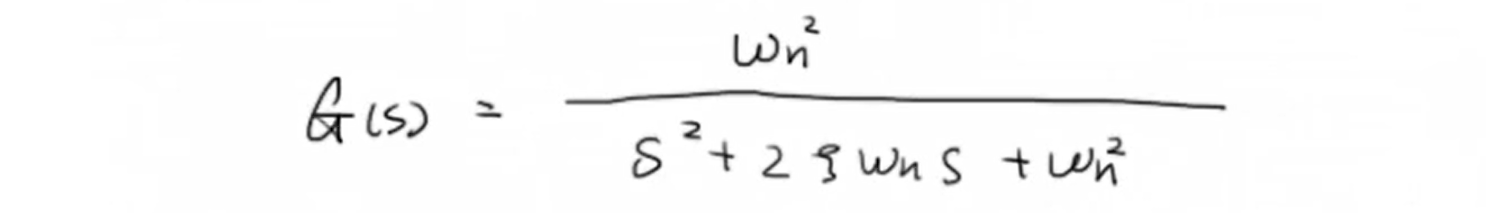
3 计算二阶系统频率响应
代入 (jomega) 求其频率响应:

3.1 振幅响应
求其模长,值得注意的是,前面为了简化计算我们令 (Omega = frac{omega}{omega_{n}}):
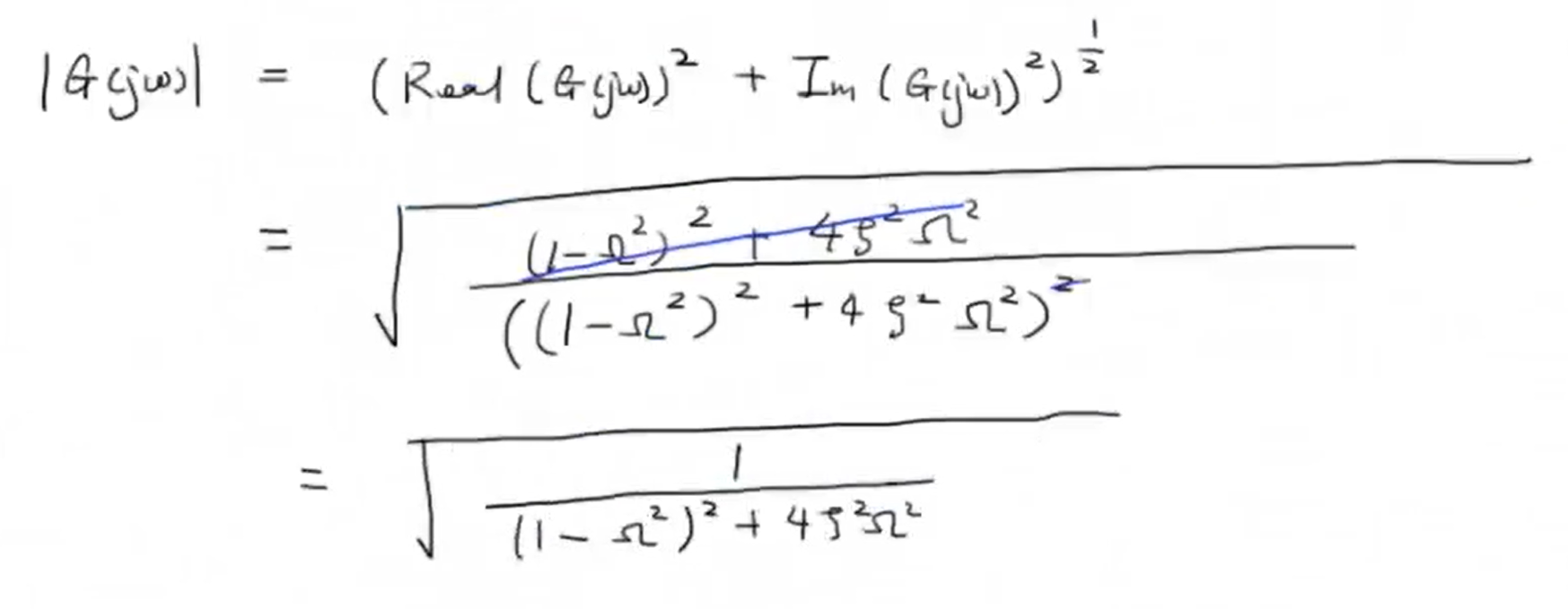
通过化简后的表达式进行分析,先分析三种特殊情况,我们发现有一下规律:
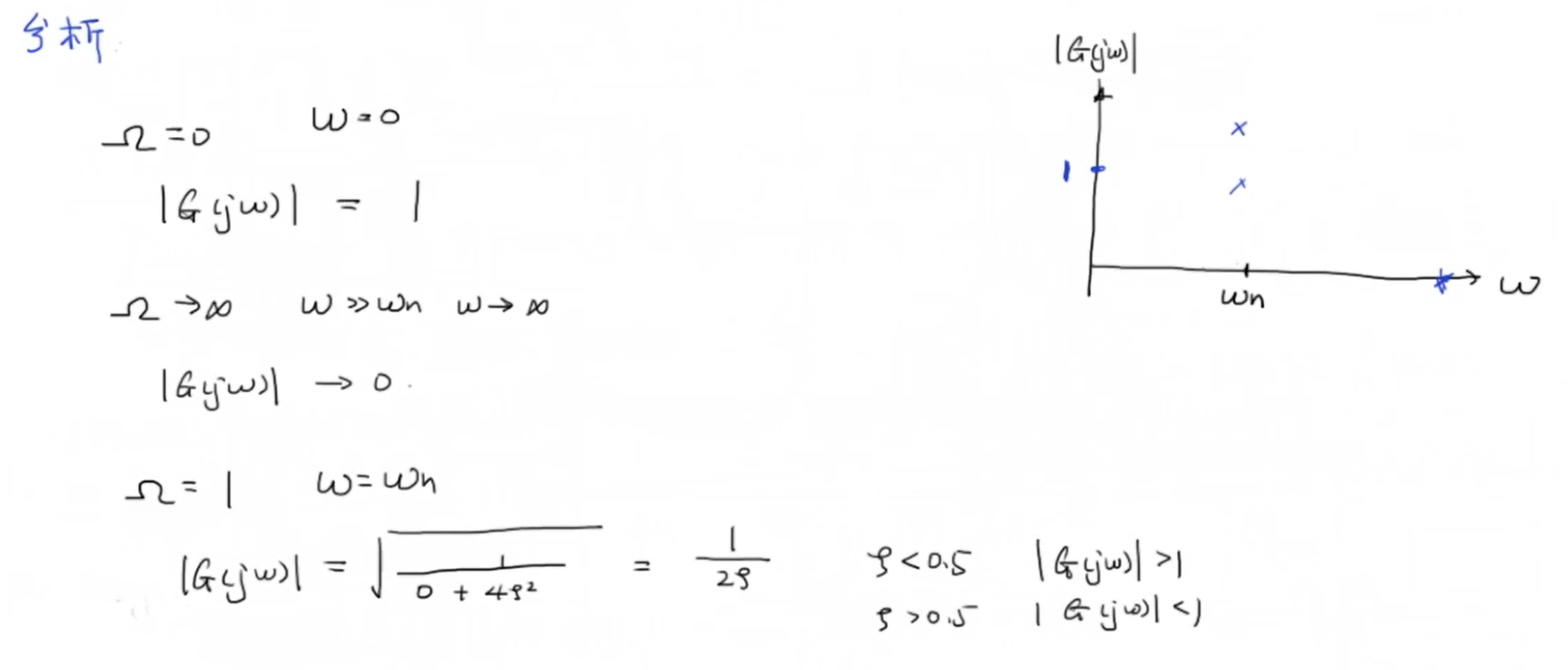
进一步分析,我们发现当 (omega=omega_n) 时的幅值相应是阻尼比的反比例函数,当阻尼比小于0.5时这个值将会比1大,这代表着函数可能存在一个极大值点。我们通过对 (|G(jomega)|) 分母求导来求这个极值点:
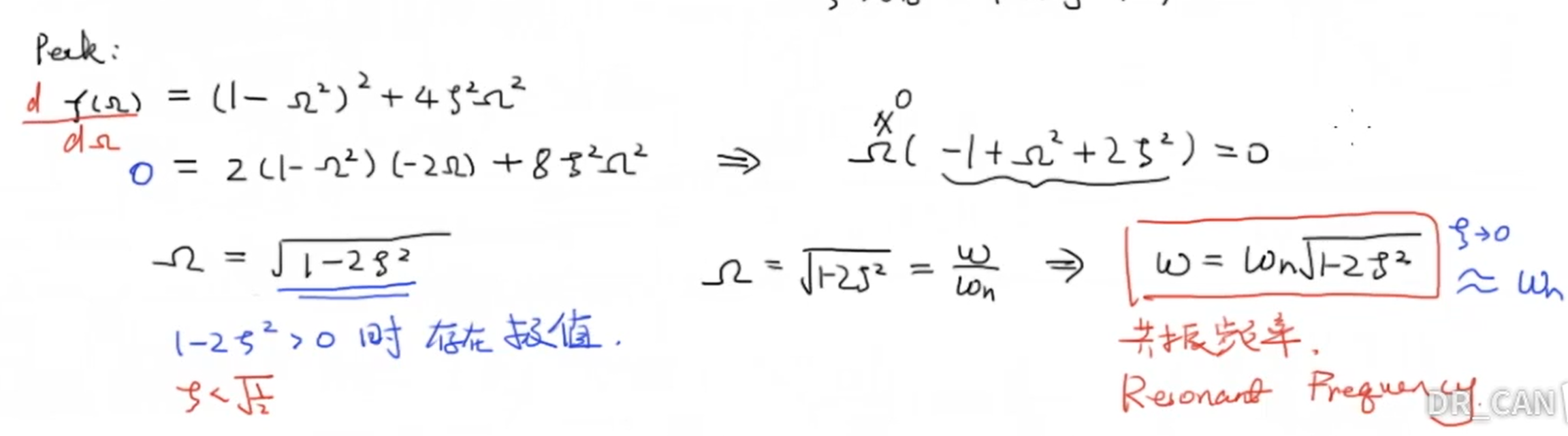
我们发现,当系统阻尼比 (zeta<sqrt{0.5}) 时,系统存在一个极大值点 (Omega = sqrt{1-2zeta^2}) 。我们定义这个极大值点对应的频率 (omega = omega_nsqrt{1-2zeta^2}) 为系统的共振频率。
进一步地,我们将 (omega = omega_nsqrt{1-2zeta^2}) 代回 (|G(jomega)|) 可以得到振幅响应的极大值:
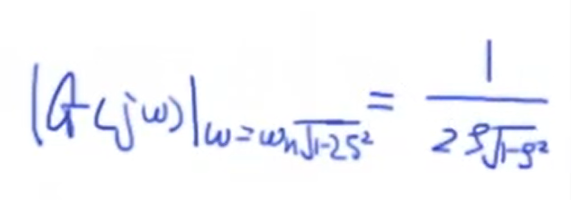
通过这个式子我们发现,当系统阻尼比较小的时候,如果系统输入频率在其固有频率或共振频率((zeta=0) 时 (omega = omega_n))附近时,振幅响应非常剧烈,甚至趋于无穷。这是因为外力将系统本身的震动潜能激励起来了,不同的系统的共振频率会有所不同,他们的共振效果也会有所不同。